A en perdre la boule - Soufflez dans le ballon

Descartes et les Mathématiques Immerger une bille Situation expérimentale : immersion d'une bille dans un cylindre - étude mathématique à l'aide d'une calculatrice TI-92
Sommaire I Énoncé du problème II Solution III Animation TI-92 IV Les programmes	Stage « Mathématiques et informatique » - Ouagadougou février 1999 Problème posé dans la publication APMEP n^o 27 - 1979 « Pour une mathématique vivante en seconde »
I. Énoncé du problème Un récipient en forme de cylindre circulaire droit de rayon r contient une quantité donnée de liquide. Des billes d'acier sphériques, de rayons divers, sont posées tour à tour à l'intérieur du récipient. On cherche pour quelles valeurs a du rayon le niveau du liquide affleure exactement le sommet de la bille.
II. Solution Pour l'étude, on suppose que les billes sont des sphères dont le rayon variable sera noté a. Données numériques proposées pour l'étude détaillée d'une situation : rayon du tube r = 5 cm (soit une valeur de 10 cm pour le diamètre d du cylindre) et v = 300 cm³ le volume de liquide contenu dans le tube. Réalisons l'expérience avec des billes de divers diamètres. Deux premières billes de diamètres 3 cm et 7cm donne les réponses que les élèves attendent : la bille est immergée lorsqu'elle est petite et émergée lorsqu'elle est plus grande. Mais pour une dernière bille de rayon 5 cm : RUPTURE… : la nouvelle bille est à nouveau immergée lorsqu'elle est grosse… Cet exercice est proposé dans de nombreux manuels de S. Dans l'ouvrage de TS de mon lycée, il est présenté avec un niveau d'eau insuffisant qui simplifie l'utilisation du théorème des valeurs intermédiaire, mais supprime l'intérêt du paradoxe !
Cas d'immersion complète de la bille Lorsque la bille est complètement immergée ou affleure, le niveau h atteint par le liquide est alors le même que si le récipient contenait uniquement un volume de liquide obtenu en ajoutant le volume de la bille de rayon a au volume v donné (300 cm³ dans la situation étudiée). Ce volume correspond à celui d'un cylindre droit de rayon r (5 cm dans la situation donnée) et de hauteur h, à savoir πr² h. On obtient ainsi l'égalité : + v = πr² h. On en déduit la valeur du niveau atteint h = + . représente la hauteur du niveau d'eau dans le tube vide. Notons que cette situation se produit lorsque le rayon de la bille est nul ou suffisamment petit.
Réponse à la question posée La bille est tout juste recouverte lorsque le niveau atteint par le liquide est égal au diamètre de la bille, c'est-à-dire 2a. D'après la formule obtenue pour le cas d'immersion complète (qui est ici tout juste réalisé), il vient : 2a = + . La TI-92 ne sait pas résoudre directement cette équation. Il s'agit d'une équation qui se ramène au troisième degré, dont on s'intéresse aux solutions comprises entre O et 2r (le maximum correspond au diamètre de la bille égal à celui du cylindre). En l'aidant un peu en simplifiant les dénominateurs, en affectant 5 → r et 300 → v ; elle sait alors la résoudre avec un message d'avertissement curieux « attention : autre solution possible ». Il y a donc, à la grande surprise de tout observateur qui ne connaît pas encore le phénomène, deux valeurs positives a₁ = 2,19 et a₂ = 4,73 pour lesquelles la bille est tout juste submergée. La troisième solution est négative et sort donc du champ qui nous intéresse. Conclusion : il est facile de concevoir la première solution : une bille de petite taille est recouverte, puis en grossissant affleure et dépasse le niveau du liquide. Il est moins facile de réaliser que pour la deuxième solution, une bille de grande taille occupe la majeure partie du vase : dans ce cas le liquide ne trouvant plus de place entre le cylindre et la bille, submerge à nouveau complément la bille.
III. Animation TI-92 Le programme graphique ballon(r, v) permet d'obtenir une animation du problème.
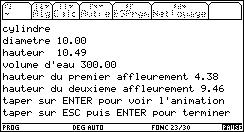
	Un premier écran texte (visible à partir de home avec la touche bascule F5) donne les diamètres des billes pour lequel a lieu l'affleurement. La touche ENTER permet de passer au mode graphique. (Dans l'état actuel du programme vérifier dans l'éditeur de fonctions ¨y= qu'il n'y a pas fonction active : F4 pour les dévalider.)
Voici quelques étapes de l'animation :

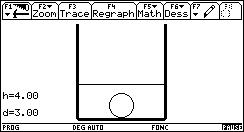
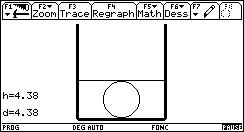
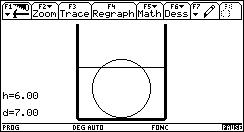
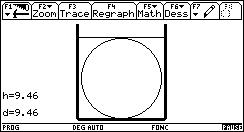
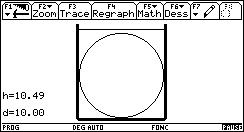
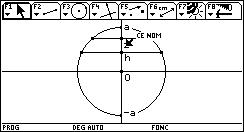
	Cette version ne donne pas la valeur exacte du niveau h lorsque a est compris entre a₁ et a₂. Le programme cherche la hauteur h virtuelle si toute la bille était recouverte et enlève le volume de calotte virtuelle qui émerge. Ce calcul ne doit pas être trop loin du résultat. Le calcul du volume se fait intégrant l'aire S(z) = π(a²/z²) du cercle de côté z dans une sphère centrée à l'origine. Il suffit de remplacer la borne du bas par a–h pour calculer ce volume dans notre repère où l'origine est le bas de la sphère.

Taper sur la touche ESC pour interrompre l'animation, puis touche ENTER pour sortir de la pause. Une deuxième partie du programme a été insérée qui permet d'obtenir des images fixes (par exemple, celles capturées ci-dessus) en tapant le diamètre d'une bille. Il est possible, par exemple, de taper 2*a1 ou 2a2 pour visualiser les affleurements. Taper ENTER pour sortir de la pause et revenir à la saisie. Taper 0 puis F5 ou ¨home pour terminer le programme.
IV. Les programmes Le programme ballon appelle trois sous-programmes initwind, initcyl et balle à placer dans le même répertoire de la calculatrice. Voici les programmes de la TI-92 plus en version française exportés par le logiciel Ti-graph-link :
ballon(r,v) Prgm Local h,pas,esc,rac,md2 (v+4/3πr^3)/(πr^2) → h If h<2r Then : 2r → h : EndIf zéros(4πa^3/3+v-π2ar^2,a) → rac EffES captMode("Afficher chiffres") → md2 défMode("Afficher chiffres","FIXE 2") Disp "cylindre" Disp "diamètre "&chaîne(approx(2r)) Disp "hauteur "&chaîne(approx(h)) Disp "volume d'eau "&chaîne(approx(v)) If dim(rac) &ge 2 Then If rac[2] ≤; 2r Then rac[2] → a1 Disp "hauteur du premier affleurement "&chaîne(approx(2a1)) Else 2r+1 → a1 EndIf Else 2r+1 → a1 EndIf If dim(rac)=3 Then If rac[3] ≥ 2r Then rac[3] → a2 Disp "hauteur du deuxième affleurement "&chaîne(approx(2a2)) Else 2r+1 → a2 EndIf Else 2*r+1 → a2 EndIf Disp "taper sur ENTER pour voir l'animation" Disp "taper sur ESC, puis sur ENTER pour terminer" Pause	Programme ballon Un premier écran texte (visible à partir de home avec la touche bascule F5) donne les diamètres des billes pour lequel a lieu l'affleurement. Calcul de la hauteur h du cylindre contenant la bille et le volume d'eau. Le mode d'affichage est mémorisé dans md2, et 2 décimales seront utilisées dans le programme. Résolution de l'équation du troisième degré. rac tableau contenant les racines de l'équation du troisième degré. On teste la dimension de rac : si dim(rac) est égal à 1 il y aune seule racine négative (à démontrer ?) sinon il y a dim(rac)-1 racines réelles mémorisée dans a1 et a2. S'il n'y a pas deux solutions réelles a1 ou a2 sont forcées à 2r + 1.
initcyl(h,r) (ymax-ymin)/103/2 → pas pas → old_h : 0 → esc While esc≠264 For a,pas,r,pas If esc≠264 Then balle(r,v,a,pas) codTouch() → esc Else Exit EndIf EndFor If esc≠264 Then balle(r,v,r,pas) For a,r,pas,-pas If esc≠264 Then balle(r,v,a,-pas) codTouch() → esc Else Exit EndIf EndFor EndIf EndWhile Pause	Appel du sous-programme initcyl pour le dessin du cylindre. On calcule un pas égal à environ un demi-pixel. Première boucle For … EndFor qui pour a allant de 0 à r, calcule les valeurs a de « pas en pas » et appelle le programme balle. On vérifie si la touche ESC de code 264 a été frappée. Deuxième boucle For … EndFor, qui pour a allant de r à 0, calcule les valeurs a de « – pas en – pas » et appelle le sous-programme balle.
a1 → a While a>0 Input "Taper un diamètre, 0 pour terminer",a If a>0 and a≤2*r Then a/2 → a pas → old_h initcyl(h,r) balle(r,v,a,pas) Pause else 0 → a EndIf EndWhile Disp "Home : taper la touche F5" EffGraph wind(-7,7,-5,5) défGraph("Axes","AFF") SupVar old_h,a1,a2,a défMode("Afficher chiffres",md2) EndPrgm	Cette deuxième partie du programme permet d'obtenir des images fixes en tapant le diamètre d'une bille. Après « input », il est possible, par exemple, de taper 2a1 ou 2a2 pour visualiser les affleurements. Taper ENTER pour sortir de la pause et revenir à la saisie. Taper 0 puis F5 ou ¨home pour terminer le programme.
balle(r,v,a,pas) Prgm Local h,e .075 → e If a<a1 or a>a2 Then (4a^3/3+v/(π))/r^2 → h Else (4a^3/3+v/(π))/r^2 → h h-(4a^3-3ah^2+h^3)/(3r^2) → h EndIf Cercle 0,a,a Lign -r,h,r,h If pas<0 Then Cercle 0,a-pas,a-pas,0 EndIf Lign -r+e,old_h,r-e,old_h,0 Cercle 0,a,a Lign -r,h,r,h Lign -r,0,r,0 PtTexte "d="&chaîne(approx(2*a))&" ",xmin,1 PtTexte "h="&chaîne(approx(h))&" ",xmin,3 h → old_h EndPrgm	Sous-programme balle Ce sous-programme dessine la bille et le niveau d'eau. Le calcul de h, lorsque la bille est découverte, est à revoir. Je n'ai pas su résoudre l'équation du 3^e degré avec la calculatrice. Un calcul d'intégrale serait peut être souhaitable. Il doit être possible de ranger les résultats dans un tableau pour ne pas trop ralentir l'exécution de l'animation. Les instructions Cercle et Lign se terminant par le paramètre 0 sont destinées à effacer l'animation précédente. Le test sur le pas négatif permet de ne pas effacer les cercles et d'obtenir une coloration de la bille. Résultat discutable ; supprimer les deux lignes if pas>0 then… et endif pour obtenir un simple cercle.
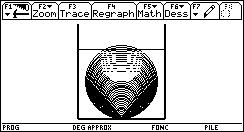
initcyl(h,r) Prgm Local e,mx,hy 0 → mx : -0.5 → ymin : h+1 → ymax (ymax-ymin)239/103/2 → hy mx-hy → xmin : mx+hy → xmax initwind(xmin,xmax,ymin,ymax) (ymax-ymin)/103 → e h+0.5 → h Line -r,0,r,0 : Line -r,0,-r,h : Line r,0,r,h Line -r-e,-e,r+e,-e : Line -r-e,0,-r-e,h Line r+e,0,r+e,h Line -r,-2e,r,-2e : Line -r-2e,0,-r-2e,h Line r+2e,0,r+2*e,h EndPrgm	Sous-programme initcyl Initcyl est le sous-programme de dessin du cylindre. En fonction de la hauteur h il calcule les coordonnées d'une fenêtre orthonormée centrée sur le bas du cylindre puis dessine le cylindre avec trois traits.
initwind(xx1,xx2,yy1,yy2) Prgm setMode("graph","fonction") ClrDraw : ClrGraph xx1 → xmin : xx2 → xmax : 0 → xscl yy1 → ymin : yy2 → ymax 0 → yscl : 2 → xres setGraph("Axes","NAFF") @défGraph("Grille","NAFF") EndPrgm	Sous-programme initwind Initwind est un sous-programme d'initialisation du mode graphique
Calculatrice TI-92 Index	Les suites en S ou ES	Petits programmes TI-92
Table des matières Google friendly	Téléchargement Télécharger ballon_ti92.zip : les programmes TI-92 zippés.
	Page n^o 19, réalisée le 1/6/2002 mise à jour le 28/7/2006

Immerger une bille

Sommaire

I. Énoncé du problème

II. Solution

Cas d'immersion complète de la bille

Réponse à la question posée

III. Animation TI-92

IV. Les programmes

Programme ballon

Sous-programme balle

Sous-programme initcyl

Sous-programme initwind

Table des matières