Descartes et les Mathématiques

Le barycentre au bac S

Trois exercices concernant le barycentre :
étude dans le plan complexe et recherche de lieux de points, avec indication de correction.

Sommaire

1. Centres étrangers 1997

2. Polynésie 1997µ

3. Inde 1999

1. Centres étrangers 1997

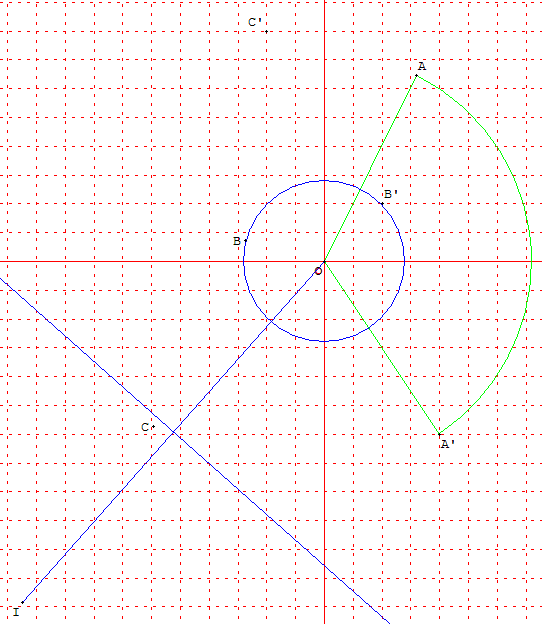
Exercice (5 points) pour les candidats ayant suivi l'enseignement de spécialité

Le plan orienté est rapporté au repère orthonormal direct (O ; , ), l'unité graphique est 1 cm.

On considère les points A, B et C d'affixes respectives :
z_A = (3 - 2) + i(3 + 2 ) ;
z_B = (- - 1) + i( - 1) ;
z_C = (1 - 4 ) + i(- 4 - ).

1. On se propose de placer les points A, B et C,
dans le repère (O ; , ), à l'aide du compas.
Pour cela, on considère la rotation R de centre O et d'angle de mesure - .

a) Donner l'écriture complexe de R.
b) Vérifier que R transforme le point A en le point A’ d'affixe :
4 - 6i.
On admettra que R transforme les points B et C en les points B’ et C’ d'affixes respectives 2 + 2i et - 2 + 8i.
c) Placer les points A’, B’, C’ puis, à l'aide du compas, les points A, B, C. (La construction du point A sera justifiée).

2.a) Calculer z_A - z_B + z_C.
b) En déduire que le point O est le barycentre du système de points pondérés {(A, 1), (B, - 1), (C, 1)}.

3. Soit l'ensemble C des points M du plan tels que :
|| - + || = || - 2 + ||.
a) Vérifier que B appartient à C.
b) Déterminer puis tracer l'ensemble C.

4. Déterminer puis tracer l'ensemble D des points M du plan tels que :
2|| - + || =|| - 3 ||.

Télécharger la figure GéoPlan bary_centre_etranger_1997.g2w

Indications

z_A - z_B + z_C = 0.

Si G est le barycentre des points pondérés (A, α) ; (B, β) et (C, γ) quel que soit le point M on a : α + β + γ = (α + β + γ) (fonction vectorielle de Leibniz).
Donc, - + =
Avec α = 1, β = −2, γ = 1, α + β + γ = 0 z_A - 2z_B + z_C = z_B, - 2 + = .
C est l'ensemble des points M du plan tels que : || - + || = |||| = OB.
C est le cercle de centre O, passant par B, de rayon 2 .

Avec α = 1, γ = −3, I barycentre de (A, 1) et (C, -3) on a - 3 = −2 .
D est l'ensemble des points M du plan tels que 2MO = 2MI, D est la médiatrice de [OI].

2. Polynésie 1997

Exercice (6 points) pour les candidats ayant suivi l'enseignement de spécialité

Partie A

Soit, dans l'espace E, quatre points A, B, C et D distincts deux à deux.

1. Montrer que ABCD est un parallélogramme si, et seulement si, D est le barycentre du système {(A, 1), (B, - 1), (C, 1)}.

2. On suppose que ABCD est un parallélogramme.

Déterminer l'ensemble (S) des points M de l'espace E tels que :|| - + || = BD.

3. On suppose maintenant que ABCD est un rectangle.

Déterminer l'ensemble (S) des points M de l'espace E tels que MA² - MB² + MC² = BD².

Partie B

On considère dans l'espace E deux parallélogrammes ABCD et A’B’C’D’ ainsi que les milieux I, J, K et L de [AA’], [BB’], [CC’] et [DD’] respectivement.

1. Montrer que L est barycentre des points I, J et K, affectés de coefficients que l'on précisera. En déduire que IJKL est un parallélogramme.

2. Soit O, Q et P les centres respectifs des parallélogrammes IJKL, ABCD et A’B’C’D’.

Montrer que O est le milieu de [PQ].

Indications

Parallélogramme, voir : le barycentre

Si G est le barycentre des points pondérés (A, α) ; (B, β) et (C, γ), quel que soit le point M, on a : α + β + γ = (α + β + γ) (fonction vectorielle de Leibniz).
Donc, - + =
S est l'ensemble des points M du plan tels que : || - + || = |||| = BD.

S est la sphère de centre D passant par B.

3. Inde 1999

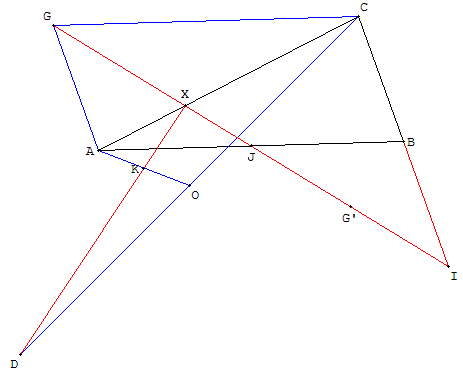
Exercice (4 points) - Candidats n'ayant que l'enseignement obligatoire

On considère un triangle ABC du plan.

1. a) Déterminer et construire le point G,
barycentre de [(A ; 1) ; (B ; - 1) ; (C ; 1)].
b) Déterminer et construire le point G’,
barycentre de [(A ; 1) ; (B ; 5) ; (C ; - 2)].

2. a) Soit J le milieu de [AB].
Exprimer et en fonction de et , puis en déduire l'intersection des droites (GG’) et (AB).
b) Montrer que le barycentre I de [(B ; 2) ; (C ; - 1)] appartient à (GG’).

3. Soit D un point quelconque du plan.
Soit O le milieu de [CD] et K le milieu de [OA].

a) Déterminer trois réels a, d et c tels que K soit barycentre de [(A ; a) ; (D ; d) ; (C ; c)].

b) Soit X le point d'intersection de (DK) et (AC).
Déterminer les réels a’ et c’ tels que X soit barycentre de [(A ; a’) ; (C ; c’)].

Télécharger la figure GéoPlan bary_inde_1999.g2w

Indications

ABCG est un parallélogramme.
B est le milieu de [CI],
J est le milieu de [GI], G’ est le milieu de [JI].

a’ = 2, b’ = 1.