Descartes et les Mathématiques

Méthode d'Euler

Construction point par point d'une courbe intégrale avec un logiciel de géométrie dynamique.

La méthode d'Euler, nommée ainsi en l'honneur de Leonhard Euler, est une procédure numérique pour résoudre par approximation des équations différentielles du premier ordre avec une condition initiale. C'est la plus simple des méthodes de résolution numérique d'équations différentielles que l'on peut utiliser dès la terminale S.

1. Introduction

Primitive

Étant donnée une fonction f définie sur un intervalle I = [x₀, x_n] et un réel y₀,
une fonction G, dérivable sur I, telle que G(x₀) = y₀ et G’(x) = f(x) pour tout x de I est une primitive de f.

Principe de Méthode d'Euler

Lorsqu'on ne sait pas trouver une formule explicite de la primitive G, la méthode d'Euler permet de calculer point par point les valeurs d'une fonction affine F telle que la représentation graphique de F soit une courbe approchée de celle de G.

Propriété de la dérivée

Si G est une fonction dérivable sur un intervalle I, f = G’ sa dérivée sur I et x_i un réel de I.

Pour tout réel h non nul et proche de 0 tel que x_i + h soit dans I on a :

G(x_i + h) ≈ G(x_i) + h G’(x_i) ≈ G(x_i) + h f(x_i)

2. Méthode d'Euler

Pour calculer des valeurs approchées d'une primitive G de f sur I = [x₀, x_n], on divise I en n intervalles et on choisit h = .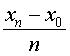

Pour la valeur initiale y₀ on a F(x₀) = G(x₀) = y₀ ce qui permet de placer le premier point A₀ (x₀ ; y₀).

Pour les n valeurs x₁ = x₀ + h, x₂ = x₁ + h…, x_n = x_n-1 + h, on calcule de proche en proche, en relation avec la propriété de la dérivée citée ci-dessus, les n valeurs approchées F(x₁), F(x₂)…, F(x_n) de G.

En effet, G est dérivable en x₀ et G’(x₀) = f(x₀) :

F(x₀ + h) = F(x₀) + h f(x₀) donc F(x₁) = y₀ + hG’(x₀) ≈ G(x₁) ; soit y₁ = y₀ + h f(x₀) et F(x₁) = y₁ ≈ G(x₁).

On recommence avec x₁ :

F(x₁ + h) = F(x₁) + h f(x₁) donc F(x₂) = y₁ + hG’(x₁) ≈ G(x₁) + hG’(x₁) ≈ G(x₂) ; soit y₂ = y₁ + h f(x₁) et F(x₂) = y₂ ≈ G(x₂).

Puis y₃ = y₂+ h f(x₂) = F(x₃) ≈ G(x₃)

Et ainsi de suite n itérations jusqu'à y_n = y_n-1 + h f(x_n-1) = F(x_n) ≈ G(x_n).

Représentation graphique

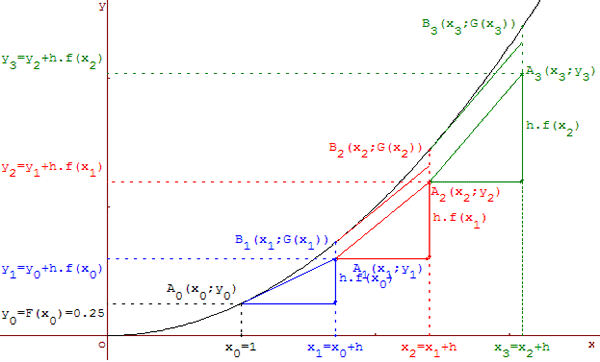
On place ensuite, avec le logiciel GéoPlan, les points A₀(x₀ ; y₀) ; A₁(x₁ ; y₁) ; A₂(x₂ ; y₂) ; … ; A_n(x_n ; y_n).

La courbe représentative de la fonction F, affine par intervalles, constituée des segments [A₀A₁], [A₁A₂]…, [A_n-1A_n] approche la courbe exacte (C) de G.

3. Étude de f(x) =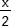

Étant donnée la fonction f(x) = et les valeurs initiales x₀ = 1 et y₀ = F(x₀) = , calculer les valeurs F(x₁), F(x₂), F(x₃)…

La représentation graphique de F par les segments [A₀A₁], [A₁A₂], [A₂A₃]… « approche » la courbe d'une primitive de f.
Augmenter n pour diminuer h et obtenir de bien meilleurs résultats.

La fonction f(x) =  a une primitive G(x) =  correspondant aux valeurs initiales x₀ = 1 et y₀ = G(x₀) = .

La courbe (C) représentative de G est placée sur le même graphe que F pour visualiser le calcul des tangentes.

Télécharger la figure GéoPlan euler.g2w

4. Étude de f(x) = 2 -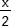

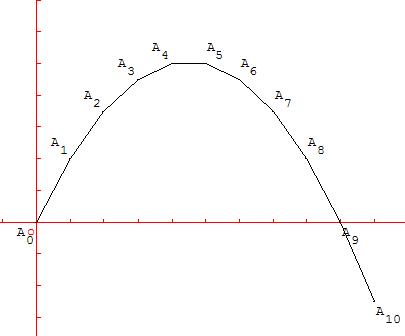
Condition initiale y₀ = F(x₀) = 0 pour x₀ = 0.

Tracé de 10 points, avec un pas h = 1.

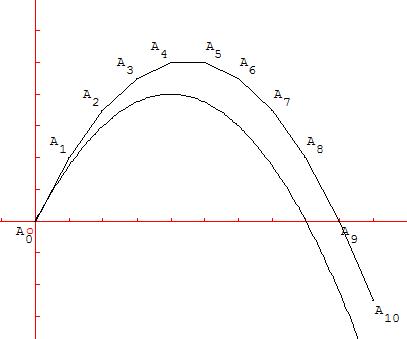
Représentation de G(x) = 2x -  ,
primitive de f telle que G(0) = 0.

5. Fonction racine

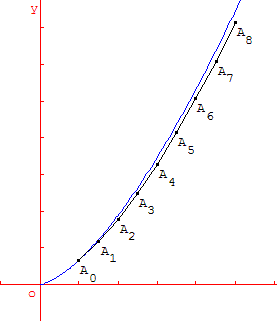
Étude de f(x) = définie sur [0, ∞[.

6. Fonction logarithme

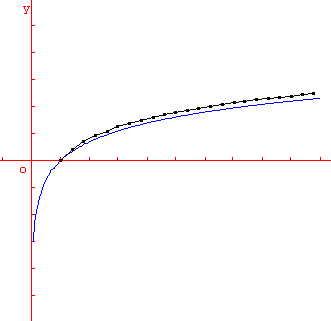
Étude de f(x) = 1/x définie sur ]0, ∞[.

On peut constater sur ces exemples qu'avec un petit pas, la méthode d'Euler donne facilement des approximations très précises.

7. Équation différentielle et méthode d'Euler

Épreuve pratique - Terminale S - 2007 - Sujet 021

Le but de l'exercice est de mettre en œuvre la méthode d'Euler pour une équation différentielle de type y’ = ay (où a est un réel donné) et d'en déduire une valeur approchée.

Compétences évaluées
Compétences TICE
– Utiliser un tableur, notamment ses fonctions graphiques ;
– Réaliser une feuille de calcul adaptée à la situation.
Compétences mathématiques
– Mettre en œuvre les connaissances sur la méthode d'Euler ;
– Déterminer la primitive d'une fonction, avec condition initiale ;
– Faire le lien entre la fonction approchée obtenue par la méthode d'Euler et la primitive : évaluer une précision.