Descartes et les Mathématiques
Problèmes de géométrie
CAPES externe de mathématiques 2007 - Épreuve sur dossier
Par Françoise Bourhis-Lainé
Sommaire
1. Triangle d'aire maximum
1. Triangle d'aire maximum
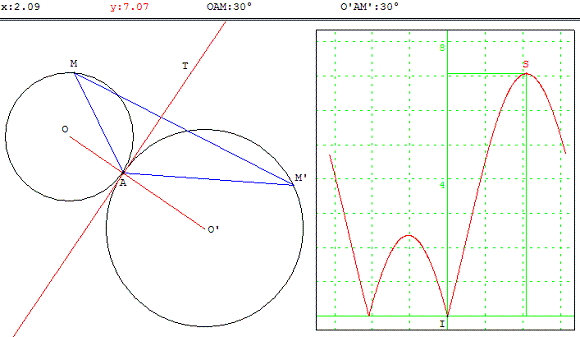
Deux cercles tangents extérieurement en A, deux points M et M’ respectivement sur l'un et l'autre. Quand l'aire MAM’ est-elle maximum ?
Variation de M’, M fixé
Télécharger la figure GéoPlan parallelisme_aire_maxi_tr_cercles_tang.g2w
Médiatrices
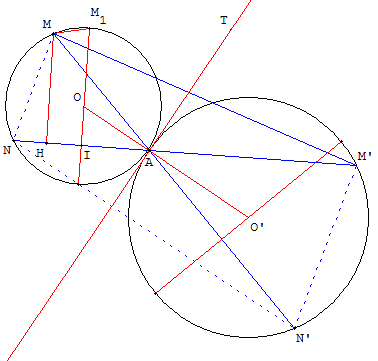
Soit N et N’ les intersections de (AM’) et (AM) avec les cercles. M1 et M2 les points d'intersection des médiatrices de [AN] et [AN’].
L'aire de AMM’ est égale à la moitié du produit de la base AM’ par la hauteur MH.
MH est plus petit que IM1. L'aire du triangle AM’M1est supérieure à l'aire de AM’M.
Placer alternativement M en M1 et M’ en M2 jusqu'à obtention de la stabilité.
Télécharger la figure GéoPlan parallelisme_aire_maxi_tr_cercles_tang2.g2w
Solution
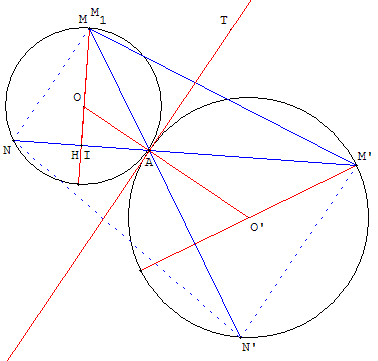
Tracer les deux droites passant par A, faisant des angles de 60° avec la tangente commune aux deux cercles (c) et (c’).
Ces deux droites recoupe les cercles en M et N’ pour la première ainsi qu'en N et M’ pour la seconde.
AMN et AM’N’ sont deux triangles équilatéraux, les côtés (MN) et (M’N’) sont parallèles à la tangente commune aux deux cercles.
Les triangles isocèles AOM et AO’M’ ont un angle de 120° et deux angles aigus de 30°.
Le triangle AMM’ a un angle en  de 120° et la tangente commune aux cercles est bissectrice de MÂM’.C'est le triangle ayant l'aire maximale,
et le triangle ANN’ est une autre solution maximale.
Démonstration
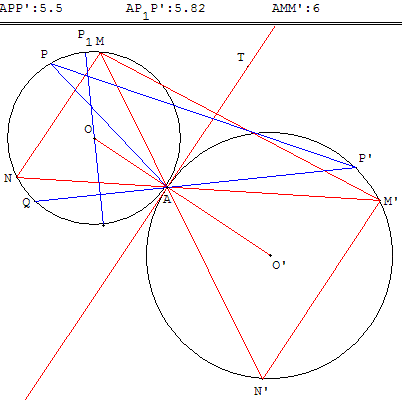
Soit APP’ un triangle avec P sur (c) et P’ sur (c’), avec P et P’ du même côté que M par rapport à la droite (OO’). Montrons que si P est distinct de M, l'aire de APP’ n'est pas maximale.
Soit Q le deuxième point d'intersection du cercle (c) avec (AP’).
La médiatrice de (AQ) coupe le cercle (c) en P. Comme on l'a montré ci-dessus, l'aire de AP’P1 est supérieure à l'aire de APP’.
Mise en équation
A(AMM’) = 
AM × AM’ sin (MÂM’)
Dans le triangle isocèle OAM : AM = 2 r cos(OÂM) = 2 r cos(α)
Dans le triangle isocèle OAM’ : AM’ = 2 r’ cos(OÂM’) = 2 r cos(β)
d'où A(AMM’) = 2 r r’ cos(α) cos(β) sin(π - α - β) = 2 r r’ cos(α) cos(β) sin(α + β)
Il faut prouver que le maximum de cos(α) cos(β) sin(α + β) est atteint pour α = β = 
.
Étudier f(x, y) = cos(x + ) cos(y + ) sin(x + y + 
)
Or f(x, y) < f(z, z) ou z est x ou y selon le minimum de |x| et |y|. À prouver, c'est vu sur GéoPlan et sur la TI92.
On est donc amené à étudier g(x) = f(x, x) = cos2(x + ) sin(2x + ).
En linéarisant, g(x) = [cos(4x + ) + 2sin(2x + )]/4 ayant pour dérivée g'(x) = cos(2x + ) - sin(4x + ) = sin( - 2x) - sin(4x + ) admet bien son maximum pour x = 0 - Dixit TI92.
Thème : problèmes de construction
Constructions avec des transformations
2. Partage d'une corde en trois
L'exercice proposé au candidat
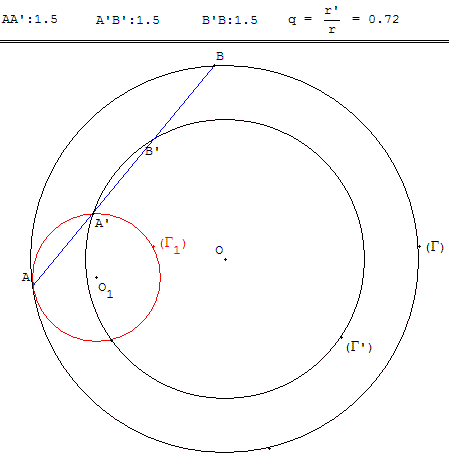
Dans cet exercice on considère deux cercles (Γ) et (Γ’) de rayons respectifs r et r’. (figure ci-dessus)
Le but de l'exercice est la construction d'une corde [AB] de (Γ) coupant (Γ’) en deux points A’ et B’ telle que : AA’ = A’B’ = B’B.
1) a) Justifier que le point A peut être choisi arbitrairement.
b) Montrer que toute corde [AB] de (Γ) coupant (Γ’) en deux points A’ et B’ on a :
AA’ = B’B.
2) On fixe un point A sur (Γ) et on note (Γ1) l'image de (Γ) par l'homothétie h de centre A et de rapport 
a) Montrer que si une corde est solution du problème existe, alors A’ ∈ (Γ1) ∩ (Γ’).
b) En déduire le nombre convenable de cordes menées de A (on discutera suivant les valeurs du rapport 
).
Le travail demandé du candidat
Q1) Dégager les méthodes utilisées dans cet exercice.
Q2) Construire la figure sur le module de géométrie d'une calculatrice et indiquer les utilisations possibles de cette construction par les élèves.
Indications
Pour une solution on AA’ = AB. D'où l'utilisation de l'homothétie h avec A’ = h(A) et (Γ1) = h(Γ),
A’ ∈ (Γ1), alors A’ ∈ (Γ1) ∩ (Γ’).
Pour construire le cercle (Γ1) trouver l'image O1 de O par h, et tracer le cercle de centre O1 passant par A.
On place ensuite B comme deuxième intersection du cercle (Γ) avec la droite (AA’).
Faire varier le cercle (Γ’).
On trouve deux solutions si < < 1 ; une solution, le diamètre de (Γ) d'extrémité A, si = .
GéoPlan
Taper S pour le cercle (Γ1) Solution,
E pour la première corde,
F pour la deuxième corde.
Télécharger la figure GéoPlan parallelisme_partage_corde_trois.g2w
Table des matières
Dans d'autres pages du site
Leçons de géométrie : problème d'incidence - parallélisme et orthogonalité
– Deux carrés autour d'un triangle
– Section d'un tétraèdre par un plan
Trisection de l'angle
Google friendly
Capes, page no 6, créée le 24/5/2007