Descartes et les Mathématiques

La géométrie dans l'espace au bac S 2014

corrigé de l'exercice

Un exercice de l'ancienne seconde qui fait scandale en terminale S !
Entre Facebook et la géométrie, comment choisir ?

bac S maths 2014 corrigé

Exercice du sujet national 2014

Choix d'un plan de l'espace pour réaliser un graphe :
      perpendiculaire commune à deux droites

Google friendly

Dans d'autres pages du site

…avec GéoSpace

GéoSpace en TS : Épreuve pratique 2007-2008

GéoSpace en TS : Épreuve pratique 2009

GéoSpace en terminale

Exercice 4 (5 points)

Candidats n’ayant pas suivi l’enseignement de spécialité

Dans l’espace, on considère un tétraèdre ABCD dont les faces ABC, ACD et ABD sont des triangles rectangles et isocèles en A.
On désigne par E, F et G les milieux respectifs des côtés [AB], [BC] et [CA].
On choisit AB pour unité de longueur et on se place dans le repère orthonormé (A,  , , ).

1. On désigne par P le plan qui passe par A et qui est orthogonal à la droite (DF).
On note H le point d’intersection du plan P et de la droite (DF).

a. Donner les coordonnées des points D et F.
b. Donner une représentation paramétrique de la droite (DF).
c. Déterminer une équation cartésienne du plan P.
d. Calculer les coordonnées du point H.
e. Démontrer que l’angle EHG est un angle droit.

2. On désigne par M un point de la droite (DF) et par t le réel tel que DM = t DF.
On note α la mesure en radians de l'angle géométrique EMG.
Le but de cette question est de déterminer la position du point M pour que α soit maximale.

a. Démontrer que ME² = t² – t + .
b. Démontrer que le triangle MEG est isocèle en M.
En déduire que ME sin() = .
c. Justifier que α est maximale si et seulement si sin () est maximal.
En déduire que α est maximale si et seulement si ME² est minimal.
d. Conclure.

Indications

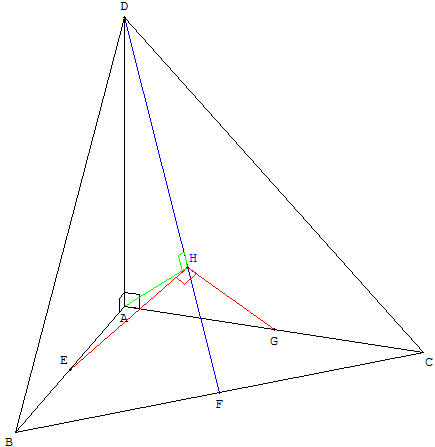
ABCD est un tétraèdre trirectangle.

1. Instructions GéoSpace

P plan passant par A et perpendiculaire à la droite (DF)
H point d'intersection de la droite (DF) et du plan P

a. Donner les coordonnées des points D et F.
D(0, 0, 1) ; F( , , 0).

b. Donner une représentation paramétrique de la droite (DF).
Soit M(x, y, z) un point de la droite (DF) et t le réel tel que = t .
((x, y, z-1) ; ( , , -1).

De l'équation paramétrique vectorielle = t , on déduit la représentation paramétrique :
x = t,
y = t,
z = 1 - t.

c. Déterminer une équation cartésienne du plan P.

P est un plan orthogonal à 2 (1, 1, -2) à pour équation x + y -2 z = d.
P passe par A : les coordonnées (0,0,0) vérifient l'équation, donc d = 0, d'où l'équation

x + y -2 z = 0.

d. Calculer les coordonnées du point H.
H est sur la droite (DF), donc t + t - 2( 1 - t) = 0 d'où 3 t = 2, soit t = .
H( , , )

e. Démontrer que l’angle EHG est un angle droit.

( - , - ,.- ) ; (- , - ,.- ).

Calculons le produit scalaire . = × (- ) + (- ) × + (- ) × (- ) = (-1/18) + (-1/18) + 1/9 = 0.
Le produit scalaire est nul, l'angle EHG des vecteurs est droit.

Remarque : AH = est la hauteur du tétraèdre rectangle isocèle et le volume (coin de cube) est .

Télécharger la figure GéoSpace national_2014_1.g3w

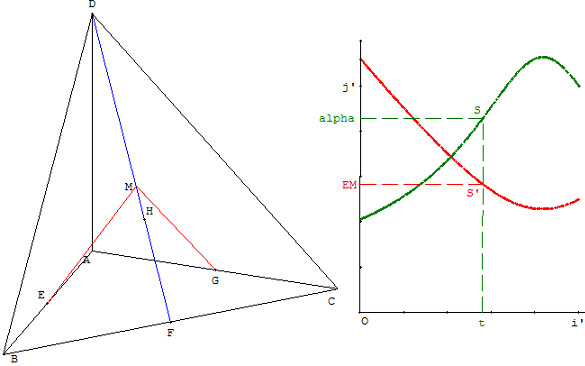
2. On désigne par M un point de la droite (DF) et par t le réel tel que DM = t DF.
On note α la mesure en radians de l'angle géométrique EMG.
Le but de cette question est de déterminer la position du point M pour que α soit maximale.

Télécharger la figure GéoSpace national_2014.g3w

a. Démontrer que ME² = t² – t + .
M ( t, t, 1 - t) ; E(, 0, 0) ; ( t - , t, 1 - t) ; d'où EM² = (t -1)² + t² + (1 - t)² = (t -1)² + t² = t² – t + .

b. Démontrer que le triangle MEG est isocèle en M.

Les points E et G sont symétriques par rapport à (AF), bissectrice de l'angle BÂC. Ils sont donc symétriques par rapport au plan (AFD), orthogonal à (ABC).
Le triangle MEG est symétriques par rapport au plan (AFD), il donc isocèle en M.

Dans le triangle rectangle isocèle AEG, de petits côtés , l'hypoténuse EG = = .
Soit I le milieu de [EG], le triangle rectangle IME a pour angle aigu IME = et sin() = IE / ME = (EG/2) / ME.
on en déduit que ME sin() = .

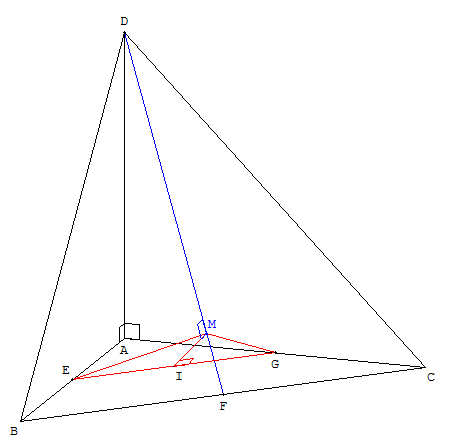
c. Justifier que α est maximale si et seulement si sin () est maximal.

En effet, les fonctions et sin(x) sont croissantes sur [0,].
En déduire que α est maximale si et seulement si ME² est minimal.

ME et sin() sont inversement proportionnelles α est maximale si et seulement si ME est minimal.

ME est positif donc la fonction carrée est croissante : ME est minimal.si et seulement si ME² est minimal.

d. Conclure.

Le minimum est celui de la parabole obtenu pour t = 5/6, soit EM² = 5/24
et M(5/12, 5/12, ).

D'où sin() = × rac(24/5) = rac(3/5), on en déduit que α ≈1,772 radian, soit 101,5°.

IM est la distance minimum entre les droites (DF) et (EG). La droite (IM) en est la perpendiculaire commune.

Le plan (MEG) d'équation x + y -2 z = est orthogonal à la droite (DF) et est parallèle au plan P.

Télécharger la figure GéoSpace national_2014_2.g3w

Note personnelle : un bel exercice. L'introduction de l'angle α est un peu artificielle et permet seulement de visualiser une fonction irrationnelle.
Pour M milieu de [DF], on aurait pu étudier la pyramide régulière AEFGM de base carrée, de volume × × = 1/24.
À part le calcul de l'angle droit EHG, réalisé ici avec le produit scalaire, toutes les notions misent en œuvre ne dépassent pas le niveau seconde et les résultats des calculs de ME et α sont donnés.

Page n^o 200, réalisée le 24/6/2014