|
 Descartes et les Mathématiques Descartes et les Mathématiques
Pyramide : volume, patron - partition d'un cube en trois ou six pyramides.
|
|
0. Pyramide
1. Coin de cube
2. 3 pyramides dans un cube
3. 6 pyramides dans un cube
4. Pyramide équilatérale de base carrée
5. Patrons de pyramides
6. Patron d'un cône
|
 Sur tablette ou smartphone, cette page lance automatiquement la version mobile GeoGebra 3D Sur tablette ou smartphone, cette page lance automatiquement la version mobile GeoGebra 3D
La pyramide dans d'autres pages du site
 Sections planes de pyramide (troisième) Sections planes de pyramide (troisième)
 Pyramide octogonale Pyramide octogonale
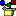 Intersection de plans dans une pyramide (seconde) Intersection de plans dans une pyramide (seconde)
|
|
Dessiner une pyramide de base carrée.
Une pyramide est un solide composé :
• d'une base polygonale,
• de faces latérales triangulaires, ayant un sommet commun, le sommet de la pyramide.
Pyramide régulière
Définition : la pyramide est régulière si la base est un polygone régulier et si la hauteur, perpendiculaire abaissée du sommet sur la base, a son pied au centre du polygone de base.
Pyramide au collège
Au collège, les pyramides étudiées auront une base rectangulaire, souvent carrée, ou bien une base triangulaire ; dans ce dernier cas, le solide est nommé tétraèdre.
Cas particuliers
Toutes les arêtes sont de même longueur :
• base triangulaire : le tétraèdre régulier,
• base carrée : la pyramide équilatérale où les faces latérales sont des triangles équilatéraux ;
le triangle ACS dans le plan diagonal est rectangle isocèle.
Autre cas particulier de pyramide régulière de base carrée :
• le triangle ACS du plan diagonal est équilatéral.
|
Formule du volume d'une pyramide
Le volume d'une pyramide (d'un tétraèdre ou d'un cône de révolution) est donné par la formule :
V =  × aire de la base × hauteur × aire de la base × hauteur
Démocrite (460-370 avant J.-C.) fut le premier à formuler l'énoncé et Eudoxe (IVe siècle) le premier à en trouver la démonstration.
Voir : tronc de pyramide
|
Pyramide régulière de base carrée
Charger la figure GéoSpace pyramide.g3w contenant la pyramide régulière de base carrée ABCD et de sommet S.
Tracer les diagonales du carré de base et le milieu O.
Tracer la hauteur [OS].
 Figure 3D dans GeoGebraTube : pyramide de base carrée Figure 3D dans GeoGebraTube : pyramide de base carrée
|
Pyramide équilatérale de base carrée
Pyramide régulière de base carrée, telle que les faces latérales soient des triangles équilatéraux.
Toutes les arêtes sont de même longueur.
 Télécharger la figure GéoSpace pyramide_equi.g3w Télécharger la figure GéoSpace pyramide_equi.g3w
 Figure 3D dans GeoGebraTube : pyramide de base carrée - plan diagonal Figure 3D dans GeoGebraTube : pyramide de base carrée - plan diagonal
Selon le triangle ACS du plan diagonal, cocher les cases :
• triangle rectangle isocèle,
• ou triangle équilatéral.
|
|
Visualiser la partition d'un cube en 3 pyramides à bases carrées, au total ayant le même volume que le cube.
Pour cela, on va partir du cube initial ABCDEFGH, définir les trois pyramides de même sommet E et de bases respectives les trois faces ABCD ; BCGF et HDCG du cube.
|
|
|
|
|
|
|
|
On vérifie que le volume de chaque pyramide est bien V = 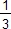 × a3 = × a3 = 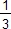 × a2 × a = × a2 × a = 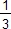 × Sbase × hauteur. × Sbase × hauteur.
 Figures 3D dans GeoGebraTube : trois pyramides inscrites dans un cube Figures 3D dans GeoGebraTube : trois pyramides inscrites dans un cube
|
|
Dans un cube de centre I, visualiser la partition 6 pyramides régulières de bases carrées les faces carrés, de sommet I.
Les six pyramides ont le même volume.
|
|
|
|
|
|
|
Par symétrie on peut compléter ces trois pyramides pour obtenir une partition du cube en six pyramides de même volume.
On retrouve encore le volume de la pyramide V = 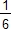 × a3 = × a3 = 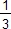 × a2 × × a2 × 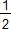 a = a = 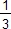 × Sbase × hauteur. × Sbase × hauteur.
 Figures 3D dans GeoGebraTube : six pyramides inscrites dans un cube Figures 3D dans GeoGebraTube : six pyramides inscrites dans un cube
|
|
|
|
Dessiner une pyramide à base carrée.
SABCD est une pyramide régulière de face carrée ABCD.
Les quatre autres faces sont des triangles équilatéraux.
Quel est l'angle des arêtes (SA) et (SC) ?
Construction avec GéoSpace
Construire un carré de côté a. Ses diagonales [AC] et [BD] se coupent en H. La hauteur (d) est la droite issue de H, perpendiculaire au plan ABC. S est un des points d'intersection de la hauteur (d) et de la sphère de centre A et de rayon a.
CHS est un triangle rectangle isocèle d'hypoténuse a : la hauteur SH est alors égale à a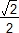 . .
|
Plan diagonal
Une vue de face du triangle ACS dans le plan diagonal (touche F avec GéoSpace) permet de conjecturer que l'angle ASC est droit.
En effet, si a est la longueur d'une des arêtes de la pyramide, on remarque que ABC est un triangle rectangle isocèle de petits côtés a et d'hypoténuse AC.
Le triangle ASB a deux côtés de longueur a et un troisième côté AC.
Il est isométrique à ABC : ASB est rectangle en S.
 Figure 3D dans GeoGebraTube : pyramide de base carrée - plan diagonal Figure 3D dans GeoGebraTube : pyramide de base carrée - plan diagonal
Cocher la case triangle rectangle isocèle.
|
|
Les trois premiers sommets appartenant à une même face du polyèdre définissent la face principale du patron et le plan dans lequel sera situé le patron lorsqu'il sera complètement ouvert ; les autres faces s'articulent autour de cette face.
En pratique si le polyèdre est une pyramide ABCDS, donner (lors de la création) en premier la liste des sommets de la future base principale ABCD dans cet ordre.
|
Patron d'une pyramide de base carrée
 Figure 3D dans GeoGebraTube : patron de pyramide de base carrée Figure 3D dans GeoGebraTube : patron de pyramide de base carrée
|
Patron d'un tétraèdre ABCS
 Figures 3D dans GeoGebraTube : tétraèdre de base un triangle équilatéral, Figures 3D dans GeoGebraTube : tétraèdre de base un triangle équilatéral,
patron d'un tétraèdre
|
|
Dans le menu « Créer>Solides », choisir l'option « Patron d'un polyèdre ». Le coefficient d'ouverture du patron est une variable réelle libre, m dans mes exemples, comprise entre 0 et 1 ; si elle est égale à 1 le patron est plan, si elle est égale à 0 le patron coïncide avec le polyèdre.
Pour ouvrir un patron par étapes, il suffit de piloter cette variable au clavier, en faisant varier m de 0 à 1.
|
|
|
|
Avec GéoSpace, il n'est pas possible de créer un patron de cône.
La même méthode que celle du cylindre, vue en cinquième, permet de l'approximer.
On obtient le polyèdre suivant :
 Figure 3D dans GeoGebraTube : cône de révolution Figure 3D dans GeoGebraTube : cône de révolution
|
Avec la touche F7 placer le plan (yOz) de face.
La figure est pilotable au clavier : appuyez sur les flèches de déplacement pour ouvrir le patron en faisant varier le coefficient d'ouverture m de 0 vers 1.
|
|
Dans d'autres pages du site
 Ces figures avec GeoGebra 3D Ces figures avec GeoGebra 3D
 …avec GéoSpace …avec GéoSpace
 …avec GeoGebra 3D …avec GeoGebra 3D
 GeoGebra en 5e : Prisme, cylindre GeoGebra en 5e : Prisme, cylindre
|
Yahoo
Téléchargement
 Télécharger geospace_quatrieme.doc : ce document au format « .doc » Télécharger geospace_quatrieme.doc : ce document au format « .doc »
 Télécharger geospace_quatrieme.pdf : ce document au format « .pdf » d'Adobe Acrobat Télécharger geospace_quatrieme.pdf : ce document au format « .pdf » d'Adobe Acrobat
Google considère l'URLcomme une erreur de type "soft 404".
Copyright 2005 - © Patrice Debart |
|
|
Page no 85, réalisée le 5/9/2005
mise à jour le 23/4/2010
|
 Descartes et les Mathématiques
Descartes et les Mathématiques![]() Sur tablette ou smartphone, cette page lance automatiquement la version mobile GeoGebra 3D
Sur tablette ou smartphone, cette page lance automatiquement la version mobile GeoGebra 3D![]() Sections planes de pyramide (troisième)
Sections planes de pyramide (troisième)![]() Intersection de plans dans une pyramide (seconde)
Intersection de plans dans une pyramide (seconde)
![]() × aire de la base × hauteur
× aire de la base × hauteur
![]() Figure 3D dans GeoGebraTube : pyramide de base carrée
Figure 3D dans GeoGebraTube : pyramide de base carrée
![]() Télécharger la figure GéoSpace pyramide_equi.g3w
Télécharger la figure GéoSpace pyramide_equi.g3w![]() Figure 3D dans GeoGebraTube : pyramide de base carrée - plan diagonal
Figure 3D dans GeoGebraTube : pyramide de base carrée - plan diagonal

















