|
La calculatrice donne les principales valeurs remarquables, le coefficient de corrélation, l'équation de la droite
de régression Dy / x. On peut obtenir un graphique et une estimation permettant de prévoir
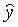 en fonction de x ou en fonction de x ou 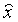 en fonction réciproque de y.
en fonction réciproque de y.
V.a. Calcul des valeurs caractéristiques
Dans le mode STAT, utiliser les options CALC puis 2VAR.
Moyennes
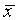 = = 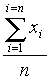 = = 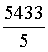 ≈1086
≈1086 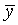 = =  =
= 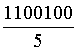 ≈ 220 038. ≈ 220 038.
Variances et écarts-types
Noter les valeurs trouvées sur l'écran de la calculatrice :
V(X) = 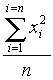 − − 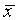 2
= 2
= 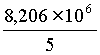 − 10862 ≈ … ; − 10862 ≈ … ;
V(Y) = 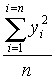 − − 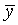 2
= 2
= 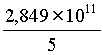 − 2200382 ≈ … ; − 2200382 ≈ … ;
∑x = 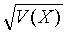 ≈
678,6 ∑y = ≈
678,6 ∑y = 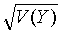 ≈
92 587 (notés par Casio x∑n et y∑n et à ne pas confondre avec x∑n−1 et y∑n−1
où les calculs sont modifiés par une division par n−1.) ≈
92 587 (notés par Casio x∑n et y∑n et à ne pas confondre avec x∑n−1 et y∑n−1
où les calculs sont modifiés par une division par n−1.)
Covariance
∑xy = 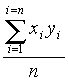 − − 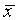 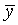 = =
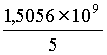 − 1086 × 220 038 ≈ … − 1086 × 220 038 ≈ …
Pour le calcul des variances et de la covariance, sans éteindre la calculatrice, quitter les STAT avec la touche MENU, choisir le Mode RUN, la touche VARS puis l'option STAT.
Enfin, la variable X et l'écart-type x∑n x2 suivi de EXE. La calculatrice affiche ∑x2 :
x∑ n2 460489,84
à recopier ci-dessus dans V(X) = … ≈ 460 490.
Puis touche EXIT et choisir la variable Y et le calcul de y∑n x2 suivi de EXE. La calculatrice affiche ∑ y2 à recopier ci-dessus dans :
V(Y) = … ≈ 8,572 ×109.
De même, pour le calcul de la covariance utiliser la variable Y puis X, en mémorisant l'effectif n :
∑ xy ÷ 5 − 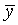 × EXIT X × EXIT X 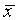 EXE EXE
Casio affiche : ∑ xy ÷ 5 − 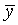 × × 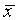 62030747 62030747
Soit ∑xy = … ≈ 6,203 × 107
V.b. droite de régression
Revenir au mode STAT, choisir CALC ou GRPH, puis REG et X.
Explications à fournir
La droite de régression a pour coefficient directeur :
a = 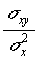 ≈
≈ 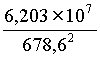 ≈ 134,7.
≈ 134,7.
La droite passe par le centre de gravité G(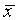 , , 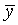 )
à représenter sur le graphique ; son équation est : )
à représenter sur le graphique ; son équation est :
y − 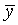 = a (x − = a (x − 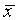 ). ).
Le coefficient constant est b = 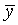 − a − a 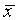 ≈ 73667. ≈ 73667.
La droite de régression de y en x a pour équation : y = 134,7 x + 73677.
Mémorisation des coefficients
Après l'exécution des calculs de la régression avec la
touche MENU, choisir le mode calcul RUN. Avec la touche VARS choisir F3 les STAT puis encore F3 le mode GRPH.
Le bas de l'écran affiche les coefficients a et b de la droite que l'on peut mémoriser dans les variables A et B.
Placer le coefficient directeur a dans la variable A : F1 →
ALPHA A
a → A
et le coefficient constant b dans la variable B : F2 →
ALPHA B
b → B
Il est aussi possible de mémoriser l'équation dans l'éditeur de fonction avec le menu GRPH et, après
le calcul de régression REG et X, utiliser la l'option COPY.
V.c. Coefficient de corrélation
Le coefficient de corrélation r est un nombre compris entre −1 et 1. Le voisinage de 1 ou de −1 indique en principe une bonne corrélation,
sans que l'on puisse directement en dire plus. On ne peut conclure à la validité d'une corrélation qu'en fonction du contexte statistique.
r = 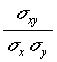 ≈
≈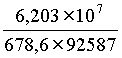 ≈ 0,987. ≈ 0,987.
Très bon taux de corrélation. Ce qui montre qu'actuellement en France, contrairement à une idée reçue,
le développement du Cinéma va de pair avec celui de la télévision.
Mémorisation du coefficient
Après l'exécution des calculs de la régression avec la touche MENU, choisir le mode calcul RUN. Avec la touche VARS choisir F3 les STAT puis encore F3 le mode GRPH.
Le bas de l'écran affiche les coefficients a, b, c … des courbes. Taper sur F6 8 pour obtenir l'écran suivant.
S'affiche le coefficient de corrélation r que l'on peut mémoriser dans la variable R :
F1 → ALPHA R
r → R
Estimation
Lorsque r est voisin de 1 ou de −1 on peut effectuer des estimations avec, en fonction du contexte, une bonne fiabilité.
Dans le mode RUN avec la touche OPTN choisir les STAT :
taper : 1000 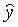 208372 208372
permet d'estimer à 208 000 le nombre de téléviseurs d'un département ou il y 1000 milliers d'entrées au cinéma.
De même : 500 000 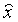 3164,9 3164,9
permet d'estimer 3 200 000 séances de cinéma dans un département ayant 500 000 postes de télévision.
V.d. Calcul de la somme des résidus
Comme au chapitre III on va placer dans list 3 les valeurs 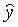 calculées en fonction de x des ordonnées des points de la droite d'ajustement d'équation y = a x + b. calculées en fonction de x des ordonnées des points de la droite d'ajustement d'équation y = a x + b.
Dans le mode STAT, après l'exécution des calculs de la régression, revenir à l'écran affichant les listes (avec, entre autres, la touche EXIT).
Avec les flèches de direction se placer sur le titre list 3 qui apparaît en inversion vidéo.
Pour le coefficient directeur a avec la touche VARS choisir F3 les STAT puis encore F3 le mode GRPH, taper F1 : affichage en bas à gauche de l'écran : a
Avec la touche OPTN choisir menu LIST et mot List et taper 1 : affichage : a list 1
taper + : affichage : a list 1 +
Pour le coefficient constant b avec la touche VARS choisir F3 les STAT puis encore F3 le mode GRPH, taper F2 : affichage : a list 1 + b
Valider avec EXE le tableau list 3 se remplit automatiquement avec les valeurs 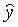 . .
Pour les résidus, carrés des écarts, se placer avec les
flèches de direction sur le titre list 4 qui apparaît en inversion vidéo.
| |
affichage |
| taper une parenthèse ouvrante : |
( |
| Avec la touche OPTN choisir menu LIST et mot List et taper 2 : |
(list 2 |
| Taper le signe de soustraction − : |
(list 2 − |
| enfin F1 mot List et taper 3 : |
(list 2 − list 3 |
| fermer la parenthèse, calculer le carré touche x2 et valider avec EXE : |
(list 2 − list 3)2
|
list 4 contient alors les résidus.
Se placer sur une case vierge, par exemple, dans list 5 et calculer leur somme : taper deux fois sur 8
: valider Sum puis 8 List et enfin taper 4 et terminer par EXE : affichage : Sum List 4
On calcule ainsi la somme des résidus égale à :
![somme[(yi-(a xi+b)]²](casio/residu.gif) ≈ 1,08 109. ≈ 1,08 109.
La droite Dy / x est donc une meilleure approximation que les ajustements précédents.
Par définition, il n'est pas possible de trouver une droite admettant un résidu moindre.
|  Descartes et les Mathématiques
Descartes et les Mathématiques![]() Mobile friendly
Mobile friendly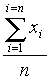 =
=  =
= 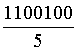 ≈ 220 038.
≈ 220 038.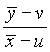 =
=
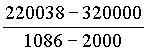 ≈ 109.
≈ 109.![somme[(yi-(a xi+b)]²](casio/residu.gif) ≈
2,60 109.
≈
2,60 109.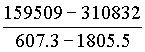 = 126,3.
= 126,3.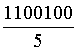 ≈ 220 038.
≈ 220 038.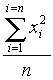 −
− 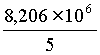 − 10862 ≈ … ;
− 10862 ≈ … ;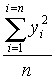 −
− 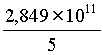 − 2200382 ≈ … ;
− 2200382 ≈ … ;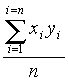 −
− 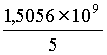 − 1086 × 220 038 ≈ …
− 1086 × 220 038 ≈ …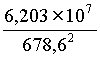 ≈ 134,7.
≈ 134,7.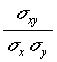 ≈
≈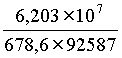 ≈ 0,987.
≈ 0,987.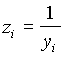 .
.