René Descartes Descartes et les Mathématiques

PROBABILITÉS et TI-92

Utilisation de la calculatrice en terminale ES, diagramme de Carroll, probabilités conditionnelles.

Sommaire

I. Premier exemple
II. Probabilités conditionnelles
III. Probabilités élémentaires

Le Programme CARROLL de la calculatrice TI-92 est une aide à traiter les problèmes faisant intervenir deux événements.

I. PREMIER EXEMPLE

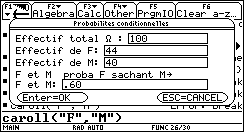	Voici le début d'un exercice classique Dans un lycée 44 % des élèves sont des filles et 40 % des élèves jouent d'un instrument de la musique. Lancer le programme carroll("F","M"). Supprimer les pourcentages et choisir 100 comme effectif pour Ω, 44 pour F et 40 pour M.
	60 % des musiciens sont des filles. C'est donc p(F/M) qui vaut 0,60. Après la pause (taper sur la touche Enter) le deuxième écran donne le diagramme de Carroll. Le recopier sur votre feuille.
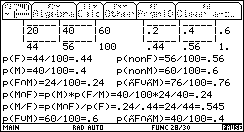	1. On interroge un élève au hasard. Quelle est la probabilité que ce soit une fille sachant jouer d'un instrument de musique ? Le troisième écran permet de calculer cette probabilité. Lire sur la calculatrice : p(M ∩F) = p(M).p(F/M) = 0,40 × 0,60 = 0,24
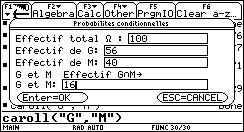	2. On interroge un garçon au hasard. Quelle est la probabilité qu'il sache jouer d'un instrument de musique ? Relancer le programme carroll("G","M") en choisissant comme effectifs 56 pour G, 40 pour M et 16 pour G ∩ M. Lire sur le dernier écran :
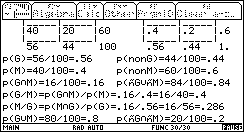	3. Les événements être une fille et jouer d'un instrument sont-ils indépendants ? non, en effet : p(M ∩ F) = 0,24 est différent de p(M).P(F) = 0,40 × 0,44 = 0,176.

II. PROBABILITES CONDITIONNELLES

Une entreprise fabrique des appareils électroniques.
La probabilité qu'un appareil fonctionne parfaitement est de 0,9.

1. On note F est l'événement « l'appareil fonctionne parfaitement ».
Quelle la probabilité de l'événement contraire de F ?

2. On fait subir un test aux appareils. On constate
– qu'un appareil qui fonctionne parfaitement est toujours accepté à l'issue du test.
– qu'un appareil qui ne fonctionne pas parfaitement peut être néanmoins accepté avec une probabilité de ¹/₁₁.
On note T l'événement « l'appareil est accepté à l'issue du test ».

a. Montrer que la probabilité de « T et F » est de 0,9.
Montrer que la probabilité de « T et » est de .

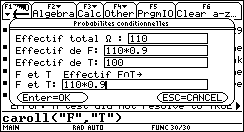Ce problème est assez difficile, car il n'y a pas de données directement accessibles. Se laisser guider par le texte.

La probabilité de est p() = 1-p(F) = 0,1.

or donc

et donc .
Cette Probabilité pouvant être le quotient « cas favorables » / « cas possibles » on est encouragé à donner un effectif de 110 à Ω et de 1 à .

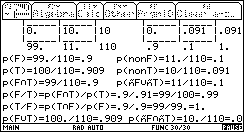b. En déduire la probabilité de T.

Lancer CARROLL("F","T"). Attention, la calculatrice ne permettant pas d'afficher , le complémentaire de F est noté non F ou Ñ F.

c. Quelle la probabilité qu'un appareil fonctionne parfaitement sachant qu'il a été accepté à l'issue du test ?

On peut lire dans le troisième écran

III. Probabilités élémentaires

La probabilité d'un événement est égale au nombre de cas favorables divisé par le nombre de cas possibles. Règle de Laplace
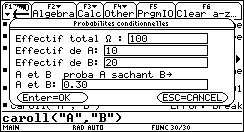	Une usine fabrique des pièces qui peuvent présenter deux sortes de défauts. 10 % des pièces présentent le défaut A. 20 % des pièces présentent le défaut B. 30 % des pièces qui présentent le défaut B présentent aussi le défaut A.
	Une pièce sort de fabrication : 1. Calculer la probabilité qu'elle présente les deux défauts. p(A ∩ B) = p(B) × p(^A/_B) = 0,20 × 0,30 = 0,006
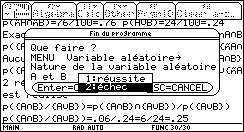
	2. Calculer la probabilité p₁ pour qu'elle présente exactement un seul défaut et la probabilité p₂ pour qu'elle soit exempte de défaut. Dans le menu final, choisir échec, puis variable aléatoire. Dans le cinquième écran, pour aucun échec lire : soit
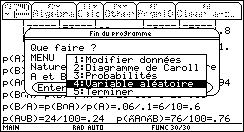	Dans le dernier écran, pour exactement 1 échec, lire : soit
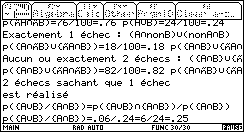
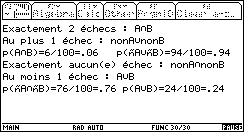
	3. Calculer la probabilité qu'une pièce présente deux défauts sachant qu'elle présente au moins un défaut. Dans le dernier écran, pour 2 échecs sachant que 1 échec, lire :