Descartes et les Mathématiques

Montrer un alignement

Exercices de géométrie plane : carré et triangles équilatéraux

Sommaire

1. Justifier un alignement de 3 points

2. Carré et deux triangles équilatéraux

    a. Vérifier un alignement
    b. Vérifier qu'un angle est plat
    c. Calculs d'angles
    d. Avec la géométrie analytique

3. Un point de concours et deux autres alignements

3.b. Deux alignements prouvés avec une rotation 

4. Alignement avec le sommet d'un triangle

5. Trois points non alignés

1. Prouver un alignement de trois points

Définition : trois points A, B, C sont alignés
si le point C appartient à la droite (AB).

Commet démontrer que trois points sont alignés :

Deux parallèles : trois points A, B, C sont
alignés si les droites (AB) et (AC) sont parallèles.

Vecteurs colinéaires : trois points A, B, C
sont alignés si les vecteurs et sont colinéaires.

Angle : trois points A, B, C sont alignés si l'angle ABC est nul ou plat.

Deux angles égaux : trois points A, B, C sont alignés
si les angles des droites (AB) et (AC) avec une troisième
droite (AD) sont les mêmes. Les angles BAD et BAC
sont égaux, on retrouve le parallélisme des droites (AB) et (AC).
Si cet angle est droit on a le cas suivant.

Deux perpendiculaires : trois points A, B, C
sont alignés si les droites (AB) et (AC) sont
perpendiculaires à une même troisième.
Voir : diamètres de deux cercles sécants ;
deux carrés - alignement avec un point de concours

Transformation : A, B et C sont alignés s'ils sont
les images de trois points alignés par une
transformation (isométrie, homothétie, similitude en TS…).
Voir : translation, orthocentre et alignement

Homothétie : alignement du centre, d'un point et de son image.

Inégalité triangulaire : l'égalité AB + BC = AC
est caractéristique de l'appartenance du point B au segment [AC].

Géométrie analytique : les coordonnées du point C vérifient
l'équation de la droite (AB). En général dans ce site, nous nous
contenterons de la preuve par la géométrie dynamique :
c'est le logiciel qui fait les calculs permettant de justifier l'alignement !

Utiliser le barycentre ou les complexes en terminale.

Géométrie du cercle : après le bac, utiliser
les propriétés de l'axe radical ou de l'axe orthique

Espace : Pour prouver l'alignement de trois points dans l'espace,
on peut montrer que ces trois points sont communs à deux plans
sécants, ils sont alors sur la droite d'intersection de ces deux plans.
Voir : règle d'incidence

2. Carré et deux triangles équilatéraux

Trouver le plus de solutions possibles à un problème :
cinq méthodes de résolution d'un exercice de la sixième à la terminale S,
sans oublier que cette activité peut faire l'objet d'une belle leçon de Capes.

2.a. Vérifier un alignement

À partir de la classe de sixième

Sur deux côtés consécutifs d'un carré construire deux
triangles équilatéraux : un à l'intérieur du carré et l'autre à l'extérieur.

Montre l'alignement des troisièmes sommets des triangles
et du quatrième sommet du carré.

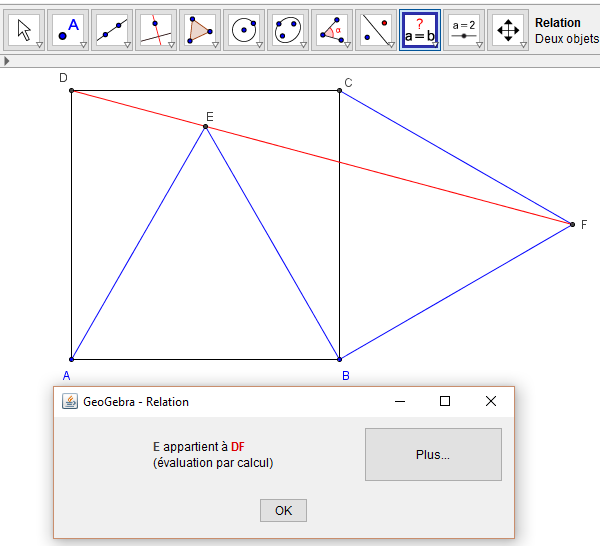
Sur du papier quadrillé, construire un carré ABCD, puis les
triangles équilatéraux ABE, à l'intérieur du carré, et BCF, à l'extérieur

Vérifier, avec la règle, que les points D, E et F sont alignés.

  – Avec GeoGebra,

Mode immédiat :

Avec la dixième icône, dans les sous menus de ABC
« insérer un texte », utiliser « relation entre deux objets »,
montrer la droite (DF), puis montre  le point E.

Programmation :

Créer le texte « Les points D, E et F sont alignés. »,
et dans les paramètre avancés de ce texte, écrire la condition :
DE + EF - DF < 0.01 inégalité triangulaire qui caractérise de
l'appartenance du point E au segment [DF]. utiliser
« relation entre deux objets », montrer la droite (DE), puis le point F, 

Figure interactive dans GeoGebraTube : carré et deux triangles équilatéraux

2.b.Vérifier qu'un angle est plat

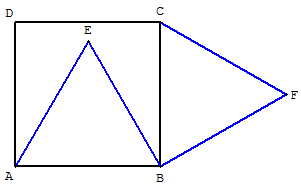
Cet exercice se traite plus simplement en utilisant les angles,
solution adoptée par la plupart des manuels de cinquième.

Solution

On procède par calcul d'angles :
DÊF = DÊA + AÊB + BÊF,
DÊF = 75° + 60° + 45° = 180°.

L'angle DEF est plat : les points D, E et F sont alignés.

Justification des angles de 75° et 45°

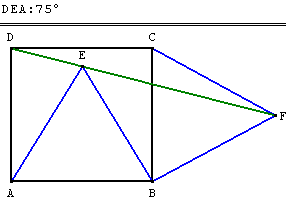
• DAE est isocèle, son angle DÂE vaut 30°,
  et donc les deux autres, en particulier DÊA, valent 75°.
• Les angles du triangle équilatéral AEB valent 60° en particulier AÊB.
• Le triangle EBF est rectangle isocèle en B et BÊF = 45°.

2.c. Deux angles égaux

Classe de cinquième

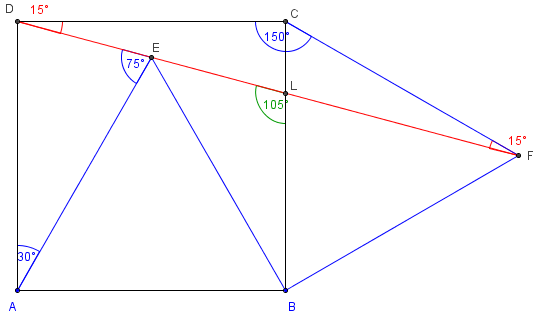
Dans cette figure, calculer les mesures des angles CDF et CDE.

Indications

Le triangle isocèle CDF a un angle au sommet de 90° + 60° = 150° .
Les deux autres angles égaux sont de (180 - 150°)/2 = 15°.

d’où CDF = 15°.

Le triangle isocèle ADE a un angle au sommet DAE de 30°.
Les deux autres angles égaux sont de 75°.

Dans l'angle droit ADC, CDF est le complémentaire de ADE,
d'où CDE = 90° − 75° = 15°.

Les angles CDF et CDE sont égaux, les points D, E et F sont alignés.

Un angle de 105°

DLB = 105°.

Dans le triangle DCL, rectangle en C, l'angle CLD complémentaire de CDL
mesure 75°.
DLB supplément de cet angle mesure 180° − 75° = 105°.

Figure interactive dans GeoGebraTube :
      carré et deux triangles équilatéraux - angles

Figure copiée sur pinterest

Un autre angle de 105°

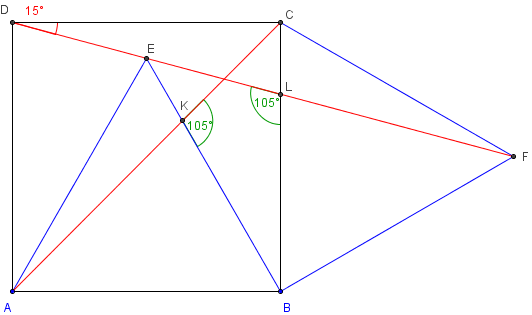
Construire un carré ABCD, puis le triangle équilatéral ABE, à l'intérieur du carré.
La diagonale [AC] du carré coupe [BE] en K.

Calculer la mesure de l'angle BKC.

Indication

Le triangle BKC a deux angles de 30° et 45°.
La somme des angles d'un triangle est 180°.

BKC = 180° - (30° + 45°) = 105°

Figure interactive dans GeoGebraTube :
      carré et deux triangles équilatéraux - angles

2.d. Avec la géométrie analytique

Classe de seconde

Méthode pas drôle du tout !

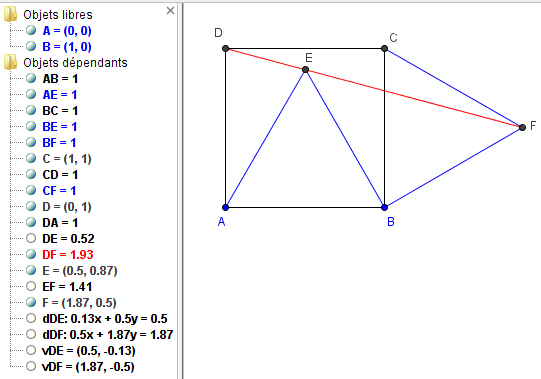
Dans le repère (A, , ), les coordonnées des points sont A(0, 0) ;
B(1, 0) ; C(1, 1) et D(0, 1).

Calculer les coordonnées des points E et F :
E(, ) ; F(1 + , ).

Calculer les coordonnées des vecteurs et :

x₁ = ;  y₁ = – 1 ; x₂ = + 1 ; y₂ = – .

Montrer que les vecteurs et sont colinéaires :
x₁ y₂ = x₂ y₁ (= – ).

Conclure : les vecteurs sont colinéaires, les points D, E et F sont alignés.

Figure interactive dans GeoGebraTube : carré et deux triangles équilatéraux

Vérifier un alignement avec GeoGebra

2.d.2. Équation de droite

Il est aussi possible de calculer l'équation de la droite (DE) :
(1 – )x + y = . Puis vérifier que les coordonnées de F vérifient cette équation.

2.d.3. Coefficients directeurs de droite

Ou encore que les coefficients directeurs des droites
a_DE = – (1 – )/() et a_DF = – ()/( + 1) sont égaux (≈ – 0,267).

2.d.4. Inégalité triangulaire

Depuis la classe de cinquième, le cas de l'égalité DE + EF = DF
est reconnue comme caractéristique de
l'appartenance du point E au segment [DF].

Pour afficher un objet ou un commentaire lorsque trois points D, E et F,
dans cet ordre sont alignés, créer les segments nommés DE, EF et DF
puis dans les propriétés avancées de l'objet, utiliser l'inégalité
triangulaire pour remplir la ligne condition pour
afficher l'objet en tenant compte des erreurs d'arrondi :
DE + EF - DF < 0,01

2.e. Avec les complexes – Terminale S

Choisir A comme origine du plan complexe
Calculer les affixes d, e et f des points D, E et F.
Conclure en vérifiant que f – d = k (e – d) avec k réel.
Conclure en étudiant f – d et e – d.

Alignement de trois points – Capes

Prouver de trois manières différentes l'alignement des trois points
Proposer des exercices où il s'agit de montrer
dans des situations diverses l'alignement de trois points.

Voir aussi point aligné sur une diagonale : parallélogramme de Pappus

3.a. Un point de concours et deux autres alignements

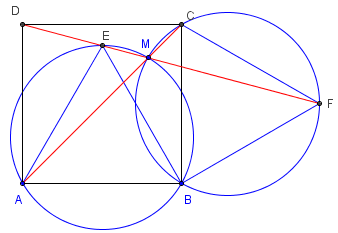
Les cercles circonscrits aux triangles
équilatéraux ABE et BCF se recoupent en M.

Le point M est aligné avec D, E et F. Il est aussi aligné avec A et C.

Figure interactive dans GeoGebraTube : carré et triangles équilatéraux

Figure copiée par pinterest

Démonstration : rotation de centre B et d'angle – 90°.

La rotation de centre B et d'angle – 90°
transforme le triangle équilatéral ABE en CBF.

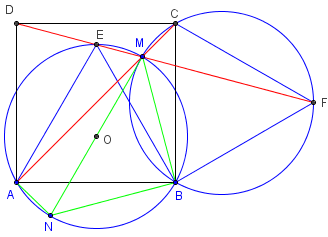
Le cercle (c) circonscrit à ABE a pour image le cercle (c’) circonscrit à CBF.

Soit N le symétrique de M par rapport au centre O du cercle (c).
AMN et BMN, inscrits dans les demi-cercles de
diamètre [MN], sont des triangles rectangles.

Par la rotation, l'image du point N, du cercle
circonscrit à CBF, est située sur le cercle circonscrit à CBF.
La droite (BN) a pour image (BM). l'image de N est sur (BM).
L'image de N, à l'intersection du cercle (c’) et de la droite (BM),
est donc le point M.

Le point M est aligné avec A et C :

L'image de la droite (AN) est la droite qui lui est
perpendiculaire, passant par C, c'est donc la droite (CA).
L'image de N, situé sur (AN), est le point M qui
est donc sur (CA). Le point M est donc aligné avec C et A.

Le point M est aligné avec D, E et F :

Le triangle équilatéral ABE et le triangle rectangle
isocèle BNM ont la droite (BO) comme axe de symétrie.
On a donc NBA = EBM = 15°. Comme EBC = 30° on a MBC = 15°.
Comme angles inscrits dans le cercle (c’) circonscrit à CBF,
on a MFC = MBC = 15°.
Le triangle isocèle CDF a pour angle au sommet CDF = 90° + 60° = 150°.
Les angles aigus mesurent (180° – 150°)/2 = 15°, soit DFC = 15°.
Comme MFC = DFC, le point M est aligné avec D et F.

3.b. Vérifier un autre alignement

Un triangle équilatéral est construit sur une diagonale d'un carré.
Le troisième sommet du triangle et les deux autres sommets
du carré sont alignés.

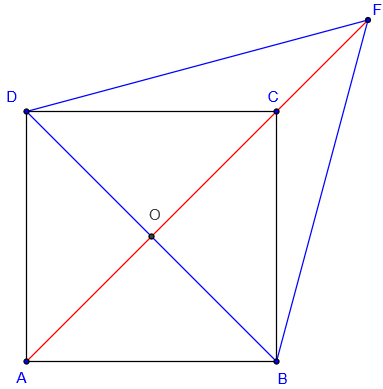
ABCD est un carré de centre E, le milieu de [BD].
BDF est un triangle équilatéral.

  – Vérifier que les points A, O, C et F sont alignés.

Indication

Dans le triangle équilatéral BDF, on a FB = FD ; F est sur la médiatrice de [BD].
Cette médiatrice est l'autre diagonale (AC) du carré.

O, milieu de [AC] et F sont donc alignés avec A et C sur la droite (AC).

Figure interactive dans GeoGebraTube :
      alignement sur la diagonale d'un carré

Compléter cet alignement : exercices de géométrie au collège

3.c. Deux alignements prouvés par une rotation

Ancienne classe de seconde

ABCD est un carré direct.
À l'intérieur placer le point E tel que ABE soit un triangle équilatéral
et à l'extérieur placer le point F tel que BCF soit un autre triangle équilatéral.
Placer le point I tel que BFIE soit un carré.

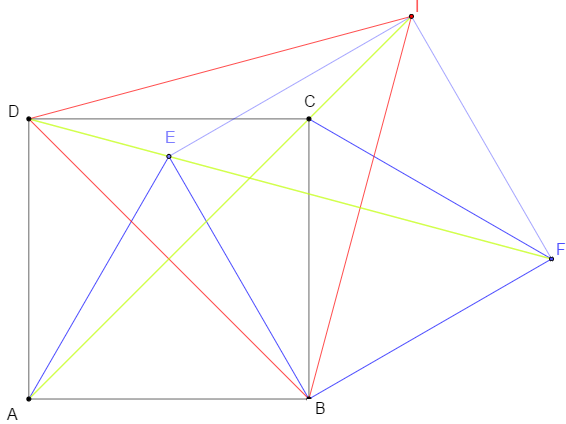
Montrer que :
  • le triangle BDI est équilatéral,
  • les points A, C et I sont alignés,
  • les points D, E et F sont alignés.

Démonstration

  • Par la rotation r(B, – ) le point A a pour image
E, le point C a pour image F, et on appelle I’ l'image de D.

L'image EBFI du carré ABCD a par l'isométrie r est
un carré.

L'image par r de [BD] est [BI] dons BD = BI
et DBI = , BDI est donc un triangle équilatéral.
L'aire du triangle équilatéral BDI est le double
de celle du triangle équilatéral ABE :
voir duplication du triangle équilatéral

  • BI est alors égal à DI, le point I est donc sur la médiatrice
de [BD], c'est-à-dire sur la droite (AC). Les points A, C et I sont alignés.

Figure interactive dans GeoGebraTube :
      alignement prouvés par rotation

Figure copiée sur pinterest

3.d. Alignement d'un autre point

Classe de seconde

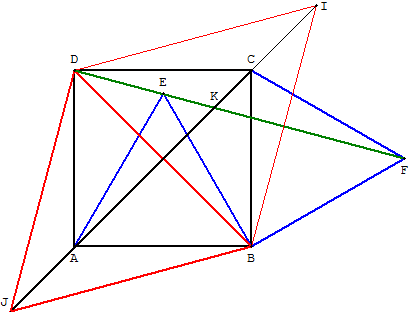
  • Placer le point J tel que BDJ soit un triangle équilatéral
contenant le point A. {J est le symétrique de I par rapport à (BD).}

J point de la médiatrice de [BD] est donc aligné avec A et C.

Par la rotation r(B, – ) le point J a pour image D.

A, C et J sont alignés, leurs images réciproques E, F et D
par la rotation r^{– 1}(B, ) sont donc alignées.

Il est possible d'utiliser cette figure pour construire
un triangle équilatéral (BDI) d'aire double
d'un triangle équilatéral donné (ABE).

L'angle de la droite (DF) et de son image (AC), par la rotation r est .

On en déduit que l'angle CDI mesure et on retrouve
les calculs trigonométriques pour un angle de ,
voir : triangle équilatéral à l'intérieur d'un carré.

Figure interactive dans GeoGebraTube :
        alignement d'un quatrième point

On retrouve le point K, appelé M ci-dessus,
comme point d'intersection des cercles circonscrits
aux triangles équilatéraux ABE et BCF.

Voir aussi : triangle équilatéral inscrit dans un carré,   aire maximale

4.a. Alignement avec le sommet d'un triangle

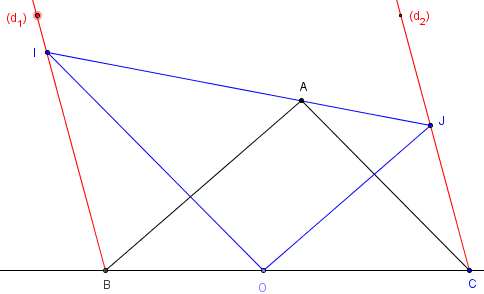
ABC est un triangle.
O un point de (BC).

Par B et C, on trace deux droites d₁ et d₂ parallèles.
La parallèle à (AC) passant par O coupe d₁ en I
et la parallèle à (AB) passant par O coupe d₂ en J.

But du problème : montrer que A, I et J sont alignés.

Figure interactive dans GeoGebraTube :
      alignement avec le sommet d'un triangle
      et démonstration par les angles inscrits

4.b. Petit théorème de Pappus

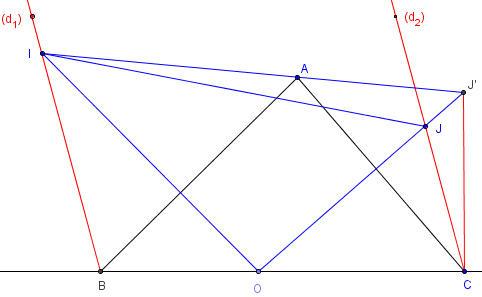
Démonstration par l'absurde

Supposons que A ne soit pas sur la droite (IJ).
Soit J’ le point d'intersection des droites (IA) et (OJ).
J’est distinct de J et n'est pas sur d₂, sinon A serait sur (IJ).

D'après le petit théorème de Pappus, les droites (BI) et (CJ’) sont parallèles.
Par C ont pourrait mener deux parallèles à d₁,
ce qui est contradictoire avec l'axiome d'Euclide.

Figure interactive dans GeoGebraTube :
    alignement avec le sommet d'un triangle - Démonstration

Géométrie analytique

Avec GeoGebra, on peut se contenter de montrer que les
coordonnées du point A vérifient l'équation de la droite (IJ).

Calculs

Choisir le point D à l'intersection de la parallèle à
d₁ passant par O et de la parallèle à (BC) passant par A.

Dans le repère (O, C, D), les coordonnées des points de la figure sont :
O(0, 0) ; A (a, 1) ; B(b, 0) ; C(1, 0) ; I(b, p) et J(1, q).
D'où (a–b, 1) et (a–1, 1)

Le parallélisme se traduit par la colinéarité des vecteurs :

= λ , d'où b = λ(a–1) et p = λ, soit p = b/(a–1) et I(b, b/(a–1)).
= ν, d'où 1 = ν(a–b) et q = ν, soit q = 1/(a–b) et J(1, 1/(a–b)).

La droite de coefficient directeur m passant par I a pour équation :
y – p = m(x–b).

Cette droite passe par J, si q – p = m(1–b),
d'où m = (a–1–b)/[(a–b)(a–1)].

On vérifie que les coordonnées de A vérifient l'équation :
y – b/(a–1) = m(x–b) !

4.c. Démonstration par les angles inscrits

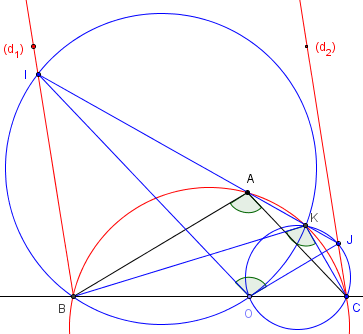
Par parallélisme des côtés : IOJ = BAC = α.

Soit les cercles circonscrits à IOB et JOC qui se recoupent en K.

Étudions les angles inscrits qui interceptent [OK] :
OIK = OBK et OJB = OCK, d'où OIK + OJK = OBK + OCK.

Les suppléments de ces sommes sont égaux, donc BKC = IOJ = α.
K est donc situé sur le cercle circonscrit à ABC.
Dans ce cercle, on a l'égalité des angles inscrits : ABK = ACK.

Montrons que K est aligné avec I et J, en calculant l'angle IKJ :
IKJ = IKB + BAC + CAJ = BOI + α + JOC = 180°, car B, O et C sont alignés.

Terminons en montrant que A est aligné avec I et J,
en calculant l'angle IAJ, en passant par la somme des angles de divers triangles  :
IAJ = IAB + α + CAJ
    = 180° – (AIB + IBA) + α + 180° – (AJC + ACJ).

En ajoutant et retranchant les angles ABK = ACK :
IAJ = 180° – (AIB + IBA + ABK) + α + 180° – (AJC + ACJ – ACK).
    = 180° – (AIB + IBK) + α + 180° – (KJC + JCK).

D'où IAJ = IKB + BKC + CKJ = 180° : I, A et J sont alignés.

Figure interactive dans GeoGebraTube ci-dessus

5. Trois points non alignés

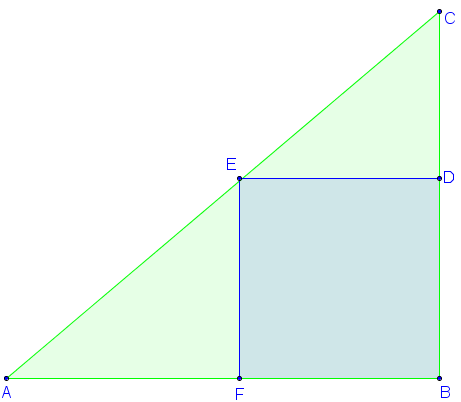
ABC est un triangle rectangle en B tel que AB =13 et BC = 11.

FBDE est un carré de côté 6, avec F sur [AB] et D sur [BC].

Le point E appartient-il au segment [AC] ?

Solution

Les points A, E et C ne sont pas alignés.

10 démonstrations

Géométrie analytique :
la droite (AC) a pour équation y = 11/13 x.
Le point E’ d'abscisse 7 de la droite a pour ordonnée 77/13 ≈ 5,9 ≠ 6.
Les coordonnées du point E ne vérifient pas l'équation de la droite (AC).

Droites non parallèles : les trois points A, E, C ne sont
pas alignés car les deux droites (AE) et (AC) ne sont pas parallèles.
Leurs coefficients directeurs 6/7 et 11/13 sont distincts.

Vecteurs : dans le repère d'origine A, les vecteurs
(13, 11) et (7, 6) ne sont pas colinéaires,
car les produits 13 × 6 et 11 × 7 sont différents.

Barycentre : si le point E était un barycentre de
A et C, un calcul avec la fonction vectorielle de Leibniz
à partir du point A montre qu'il existerait un nombre k tel que = k .
Contradiction vue ci-dessus avec les vecteurs de
coordonnées (13, 11) et (7, 6) qui ne sont pas colinéaires :
les équations 13 k = 7 et 11 k = 6 n'ont pas de solution
car 7/13 et 6/11 sont distincts.

Angles

Deux angles inégaux : les trois points A, E, C ne sont pas
alignés car les angles BAE = 40,6° et BAC = 40,2° sont distincts

Angle nul : l'angle CAE = 0,3° est différent de 0.

Angle plat : l'angle AEC = 179° n'est pas égal à 180°.

Inégalité triangulaire : la somme AE + EC n'est pas égale à AC.
Avec GeoGebra utiliser 3 décimales et
on trouve AE + EC = 17,03 distinct de AC =17,029.

Thalès : les triangles ABC et AFE ne sont pas
f semblables : 6/7 est différent de 11/13.

Homothétie : dans l'homothétie de centre A et de
rapport 7/13, le triangle ABC a pour image AFE’ distinct du triangle AFE.

Il y aurait d'autres démonstrations...

Figure interactive dans GeoGebraTube : trois points non alignés

Table des matières

Théorèmes mettant en œuvre des alignements

Théorème du trapèze

Théorème de Pappus

Théorème de Desargues

Théorème de Pascal

Théorème des trois cercles

Alignements dans d'autres pages du site

Alignement avec un point et son transformé par une rotation

Diamètres de deux cercles sécants

Alignement avec un point et son transformé dans une similitude

Deux carrés : alignement avec un point de concours

Alignement dans trois carrés consécutifs

Tiers d'un segment dans un parallélogramme

Deux triangles équilatéraux autour d'un carré

Étude de lieux géométriques

Intersection inaccessible

Construction à la règle seule

Polaire par rapport aux médianes d'un triangle

Montrer un alignement dans l'espace

Figure 3D de GeoGebraTube : montrer un alignement dans l'espace

Google friendly