
Carré inscrit dans un pentagone

 |
Carré inscrit dans un pentagone |
 |
Travaux pratiques de géométrie dynamique avec GeoGebra.Un scénario pour le lycée.
Atelier |
|
|
||
3. Carré ayant deux sommets opposés |
|
Énoncé Construire un carré aussi grand que possible à l'intérieur d'un pentagone régulier. Construction Pour construire un pentagone régulier ABCDE de côté a = 1 avec GeoGebra, créer deux points : |
1. Carré ayant deux sommets consécutifs sur le pentagone
|
Pour un point M sur [AB] et N sur les côtés [AB] ou [BC] {N = Point[penta]}, tracer le carré MNPQ. Un tel carré maximal a trois sommets sur le pentagone et la recherche peut se réorienter vers des carrés ayant deux sommets opposés situés sur le pentagone. |
2. Carré ayant deux sommets opposés sur deux côtés consécutifs du pentagone
|
Soit le point M sur [AB] et P sur le côté [BC]. Le carré MNPQ n'est pas à l'intérieur du pentagone. |
3. Carré ayant deux sommets opposés sur deux côtés non consécutifs du pentagone
|
Étudier le cas où le point M est sur [AB] et P est sur le côté [DE]. |
4. Carré inscrit dans le pentagone
|
Si trois des sommets du carré (distincts des sommets du pentagone) sont situés sur le pentagone alors les quatre sommets y sont : Un des côtés du pentagone est parallèle aux côtés du carré. |
5. Carré ayant un sommet en commun avec le pentagone
|
Carré AMNP à l'intérieur du pentagone. Trouver le carré maximal et conclure. |
|
L'angle au centre du pentagone régulier est de 72° et l'angle intérieur de 108°. Si a est la longueur du côté et r le rayon du cercle circonscrit, on a montré dans la page polygones réguliers que : D'où r = 0,85065 a. |
|
Pour un pentagone régulier ABCDE inscrit dans le cercle de rayon r, centré en O, on peut placer le point A sur (Oy) tel que ses coordonnées soient A(0, r). Dans le sens direct, le sommet suivant a pour coordonnées : B(r cos(9π/10), r sin(9π/10)). Pour construire un pentagone régulier de côté a = 1, créer deux points A et B. Dans le champ de saisie, il est aussi possible de taper directement A = (0 ; 0.85), puis B = (0.85 ; 162°). Choisir l'icône polygone régulier, sélectionnez les deux sommets consécutifs A et B et saisissez le nombre 5 dans la boîte de dialogue qui s'est ouverte ; on obtient un polygone pentagone régulier de côté 1.
|
|
Soit MNPQ un carré situé à l'intérieur du pentagone. Si au plus un des sommets (par exemple M) se trouve sur un côté du pentagone, |
|
Placer un point M sur le côté [AB], puis dans le menu contextuel de M, remplacer Point[AB] par Point[penta]. Recommencer pour le point N. Soit le point M sur [AB] et N sur le côté [BC], si P et Q sont strictement à l'intérieur du pentagone, en éloignant M ou N du sommet B, on peut trouver un carré plus grand, tant que P ou Q ne sont pas sur le pentagone. |
|
Carré ayant deux sommets opposés situés sur deux côtés consécutifs du pentagone. Soit le point M sur [AB] et P sur le côté [BC].
Le cercle de diamètre [MP] passant par N (sens direct) est situé à l'extérieur du pentagone, le point N est à l'extérieur et le carré ne convient pas. |
|
Soit le point M sur [AB] et P sur le côté [DE]. Une étude rapide montre que si on choisit M proche de B (BM < a/2),
Pour aider à la recherche avec GeoGebra, on utilise l'affichage conditionnel de la couleur de remplissage du carré : soit I le centre du carré ; la droite IN rencontre le côté [BC] du pentagone en N’ ; la couleur fond du carré est dessinée lorsque N est à l'intérieur du pentagone, si IN < IN’. Transformation par une rotation : Si les points N et P sont à l'intérieur du pentagone, on peut tracer les perpendiculaires en M à (AB) et en P à (DE). Une rotation de centre J, d'angle θ suffisamment petit, dans un sens ou dans l'autre, transforme ce carré en un carré strictement à l'intérieur du pentagone, qui n'est pas de taille maximale.
Un carré est de taille maximale si au moins trois des sommets sont situés sur le pentagone. |
|
Si trois des sommets du carré (distincts des sommets du pentagone) sont situés sur le pentagone alors les quatre sommets y sont et le carré est inscrit dans le pentagone : Prendre les points variables N sur [BC] et P sur [DE]. La recherche du carré est facilitée avec une figure de clôture :
Faire coïncider N et N1 ; conclure au parallélisme de (CD) et (NP). Un calcul d'angle démontre que le côté (CD) du pentagone est parallèle aux côtés du carré (cf. bibliographie). Exemple de construction avec une homothétie de centre A où le carré inscrit est l'image du carré ayant pour côté la diagonale [BE] :
Dans un pentagone de côté 1, le carré a pour côté 1,0604 et pour aire 1,124. dans le |
Traité de géométrie théorique et pratiqueà l'usage des artistes (1674) 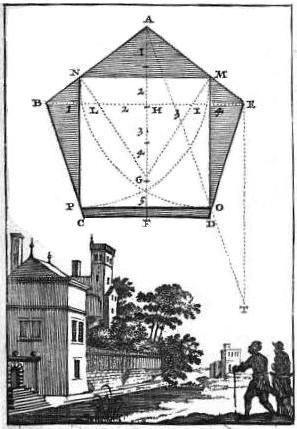 Images de Sébastien Leclerc : Traité de géométrie théorique et pratique |
 La « pratique » de Sébastien Leclerc donne les instructions pour dessiner la figure en géométrie dynamique ! Avait-il GeoGebra ? |
|
Les figures sont dessinées dans le ciel, accompagnées de croquis, montrent qu'au XVIIe, la géométrie était déjà centrée sur les problèmes concrets, en général, et l'astronomie, en particulier. | |
5.1. RechercheCarré AMNP à l'intérieur du pentagone. Recherche : déplacer le point M pour trouver le carré maximal.
5.2. Carré maximal solution
Le carré solution est l'image du carré AM’N’P’, inscrit dans le cercle circonscrit, par une homothétie de centre A. |
|
Dans ce scénario la géométrie dynamique est particulièrement pertinente. Aucune connaissance préalable n'est requise, mais les déductions ne sont pas élémentaires et il ne faut pas passer à côté de la solution : |
|
Lo Jacomo François – Les problèmes de l'APMEP – Bulletin vert no 383 – Avril 1992 | ||||
3. Carré ayant deux sommets opposés sur deux côtés non consécutifs du pentagone |
||||
Atelier APMEP |
||||
|
« Descartes et les Mathématiques » Accueil : www.debart.fr Page no 180, créée le 16/10/2011 | ||||