Descartes et les Mathématiques
Carré d'aire cinq fois plus petite
Puzzles de 5, 9, 10 ou 20 pièces dans un carré, permettant de visualiser un petit carré central.
Sommaire
1. Deux droites orthogonales menées d'un sommet au milieu d'un côté du carré
1.b. Découpage d'aires dans un carré
2. Carré d'aire 5 fois plus petite
4. Deux droites perpendiculaires dans un carré
4.b. Carré d'aire cinq fois plus petite (figure symétrique)
5. Composer un carré avec 5 carrés
6. Multiplication par 5 de l'aire d'un carré
Sur tablette numérique ou smartphone, bascule automatique vers la version mobile
1. Droites menées d'un sommet au milieu d'un côté
1.a. Deux droites orthogonales dans un carré
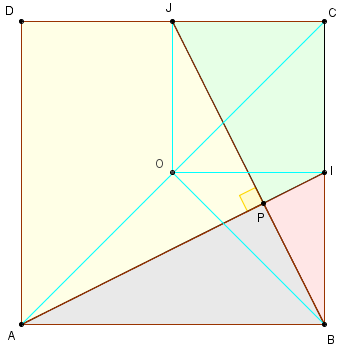
Les points I et J sont les milieux des côtés [BC] et [CD] d'un carré ABCD.
Montrer que les droites (AI) et (BJ) sont orthogonales.
Indication
Avant la réforme du lycée de 2008, en classe de seconde, on pouvait utiliser une rotation, quart de tour de centre O, milieu du carré :
Le point A a pour image B, I a pour image J, le segment [AI] et son image [BJ] sont orthogonaux.
En 1ère S, on peut encore montrer que le produit scalaire 
.
est nul.
Le triangle rectangle BPI a une aire égale au vingtième de celle du carré,
Le triangle APB et le trapèze PICJ ont même aire égale au cinquième de celle du carré,
l'aire du quadrilatère APJD est onze vingtième de celle du carré.
Figure interactive dans GeoGebraTube : droites orthogonales dans un carré - rotation
1.b. Découpage d'aires dans un carré
Les points I, J, K et L sont les milieux des côtés d'un carré ABCD.
On mène quatre droites des sommets au milieux des côtés opposés, en tournant dans le même sens.
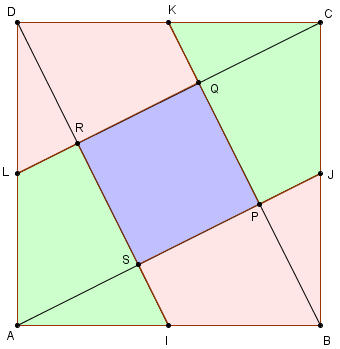
Cinq pièces de même aire
Un découpage de ABCD avec un petit carré central PQRS bordé par 4 quadrilatères d'aires un cinquième de l'aire du grand carré.
Figure interactive dans GeoGebraTube : carré et 4 quadrilatères dans un carré
Calcul d'aires de triangles
La droite (AI) est perpendiculaire à (BJ) :
D'après la propriété de Pythagore dans le triangle ABI, rectangle en B,
AI2 = a2 + 
= 
a2, d'où l'hypoténuse AI = 
a.
Le triangle BPI, rectangle en P, d'hypoténuse 
a, est semblable au triangle ABI dans le rapport 
.
Aire(ABI) = AB × BI = a × a = 
a2,
Aire(BPI) = 
× Aire(ABI) = 
a2.
Le triangle BPI a une aire égale au vingtième de celle du carré.
Par différences :
Aire(APB) = Aire(ABI) - Aire(BPI) = a2 - a2 = a2.
Aire(PICJ) = Aire(BCJ) - Aire(BPI) = a2 - a2 = a2.
Le triangle ABP et le quadrilatère PICJ ont même aire égale au cinquième de celle du carré.
Une quatrième aire : Aire (APJD) = Aire(ABCD) - Aire(APB) - Aire(PICJ) - Aire(ABI) = a2 - a2 - a2 - a2 = 11/20 a2.
Évaluation d'aires sans calcul
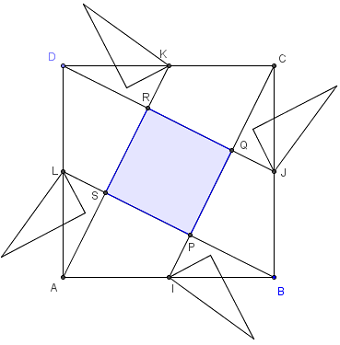
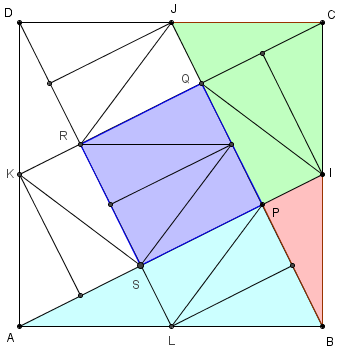
Un puzzle de 20 triangles rectangles isométriques dans un carré.
Chaque triangle comme le triangle BPI a une aire égale au vingtième de celle du carré
Le petit carré central PQRS est formé de 4 triangles, soit une aire égale au 4/20 donc 1/5 du carré
Le triangle ABP et le quadrilatère PICJ sont formés par 4 pièces ont même aire égale au 4/20 soit 1/5 de l'aire du carré.
L'aire de APJD est donc de 11/20.
Figure interactive dans GeoGebraTube : carré partagé en 20 pièces
1.c. Variante
I et J sont deux points situés respectivement sur les côtés [BC] et [CD] d'un carré ABCD tels que BI = CJ.
Montrer que les droites (AI) et (BJ) sont orthogonales.
1.d. Autre figure
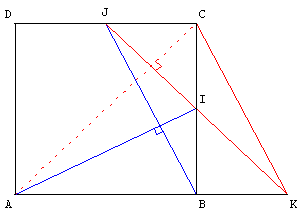
Les points I et J sont les milieux des côtés [BC] et [CD] d'un carré ABCD. Les droites (AB) et (IJ) se rencontrent en K.
Montrer que la droite (AC) est orthogonale à (IJ) et en déduire que (AI) est orthogonale à (CK).
Montrer que BKCJ est un parallélogramme et en déduire que les droites (AI) et (BJ) sont orthogonales.
Télécharger la figure GéoPlan carre_4.g2w
1.e. Hauteurs du triangle AIJ
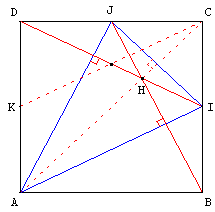
Les points I, J et K sont les milieux des côtés [BC], [CD] et [AD] d'un carré ABCD.
Les droites (DI) et (BJ) sont les hauteurs du triangle AIJ.
Médiane de l'un, hauteur de l'autre
La droite (DI) est la hauteur du triangle ADJ et la médiane du triangle CDK.
Télécharger la figure GéoPlan carre_5.g2w
Voir : calculs d'angles (avec le produit scalaire)
2. Carré d'aire cinq fois plus petite
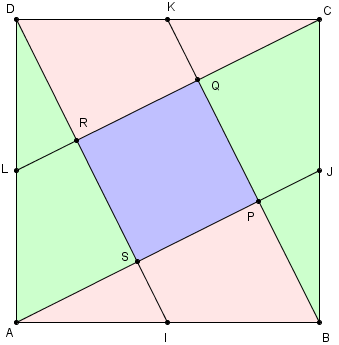
I, J, K et L sont les milieux des côtés d'un carré ABCD
Justification par une rotation
La figure est invariante par une rotation d'angle 90° autour du centre du carré ABCD.
Le quadrilatère PQRS est aussi invariant par cette rotation. c'est donc un carré.
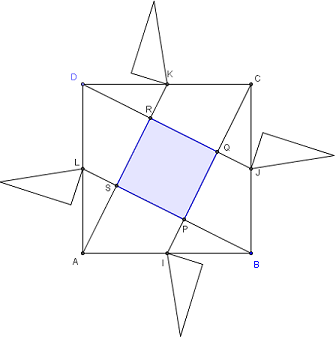
Cinq pièces de même aire
Un découpage de ABCD avec un petit carré central PQRS bordé par 4 triangles rectangles d'aires un cinquième de l'aire du grand carré.
La droite (AJ) est perpendiculaire à (BK),
calculer PQ en fonction de a,
l'aire de PQRS est égale à de l'aire de ABCD.
Figure interactive dans GeoGebraTube : carré cinq fois plus petit - 5 pièces
3. Quadrilatère PJCM
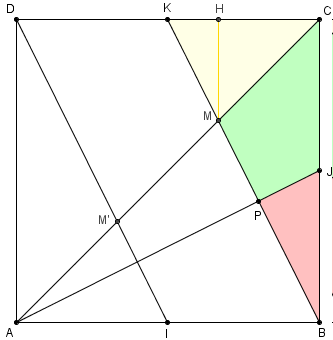
Si M est le point d'intersection de (BK) et (AC),
quelle est l'aire du quadrilatère PJCM ?
Triangle BPI
Les droites (BK) et (AJ) sont perpendiculaires Le triangle rectangle BPI a une aire égale au vingtième de celle du carré.
Étude du triangle KCM :
Dans le carré ABCD, les droites (ID) et (BK), joignant deux sommets opposés aux milieux des côtés opposés, sont parallèles et les points M et M' partagent la diagonale [AC] en trois parties égales :
voir parallélogramme et milieux.
Si H est la projection de M sur (CD), MH = 
a et
Aire(KCM) = × KC × MH = × a × a = 
a2.
Étude du quadrilatère PJCM
Par différence :
Aire(PJCM) = Aire(PJCK) - Aire(KCM)
= a2 - a2 = 
a2.
Figure interactive dans GeoGebraTube : Triangles et quadrilatère dans un carré
4. Deux droites perpendiculaires dans un carré
Indications avec le produit scalaire
Montrer que le produit scalaire 
.
est nul :
Méthode 1 : faire le calcul dans un repère en choisissant le repère canonique (A, 
, 
) ou le repère (A, 
, 
).
Méthode 2 : avec des relations de Chasles et la bilinéarité du produit scalaire, calculer
(
+ 
).(
+ ) en remarquant les deux produits scalaires nuls.
Figure interactive dans GeoGebraTube : deux droites perpendiculaires dans un carré
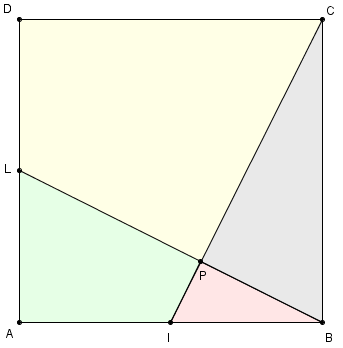
4.b. Carré d'aire 5 fois plus petite (figure symétrique)
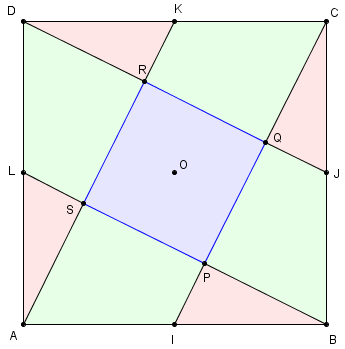
I, J, K et L sont les milieux des côtés d'un carré ABCD (longueur du côté AB = a).
Montrer que la droite (IC) est perpendiculaire à (LB),
calculer PQ en fonction de a,
Calculer la longueur PQ à l'aide du produit scalaire . en remarquant que 
est le projeté orthogonal de sur .
justifier que PQRS est un carré,
montrer que son aire est égale à de l'aire de ABCD.
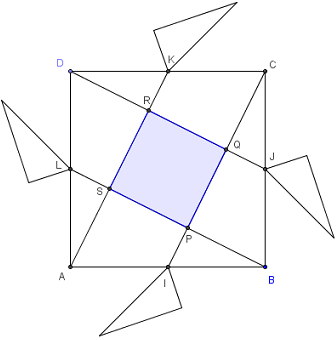
Découpage du carré
Le grand carré est la réunion de neuf pièces : le petit carré, quatre triangles dans les coins d'aire s et quatre trapèzes. Ces pièces sont isométriques par la rotation citée ci-dessus.
Le triangle ABS est un agrandissement double du triangle IBP. Son aire est dons 4s.
Par soustraction, on a : Aire(IPSA) = Aire(ABS) - Aire(IBP) = 4s - s = 3s
Le triangle ABL est formé par deux triangles d'aire s et un trapèze d'aire 3s, soit 5s.
Aire(ABL) = AB ×AL = a × a = a2 = 5s.
On a donc s = a2 et Aire(ABS) = 4s = a2.
L'aire du carré central est donc l'aire totale moins quatre fois l'aire de ces triangles : Aire(PQRS) = a2 - 4 × a2 = a2..
Figure interactive dans GeoGebraTube : carré d'aire cinq fois plus petite - 9 pièces
Figure symétrique dans GeoGebraTube : carré d'aire cinq fois plus petite - 9 pièces
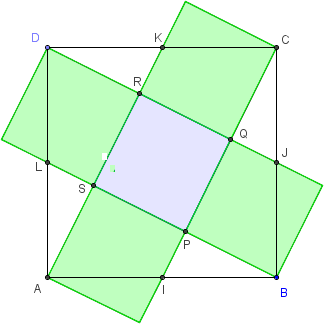
5. Composer un carré avec cinq carrés
Problème du carreleur :
avec cinq carreaux de céramique, paver un grand carré.
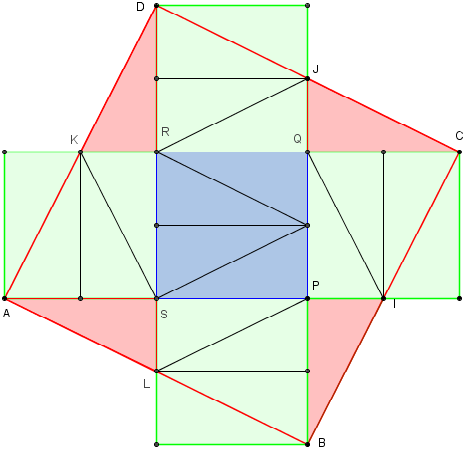
Disposer les cinq carrés autour du carré central PQRS en forme de croix suisse.
Joindre A à B, B à C, C à D et D à A, on obtient un carré ABCD .
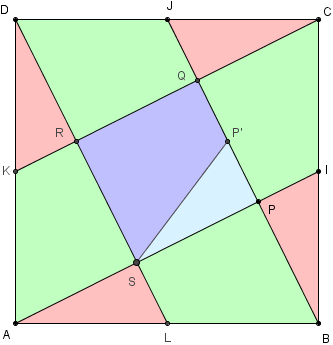
En découpant les quatre triangles extérieurs et en les portant, par symétries de centres L, I, J et K, on obtient quatre triangles rectangles ASL, BPI, CQJ et DRK isométriques.
Ils permettent de reconstituer le carré ABCD, formé par 20 triangles rectangles isométriques, d'aire égale à 5 fois l'aire de PQRS.
Figure interactive dans GeoGebraTube : Carré et croix du carreleur
Puzzle :
On reprend la figure avec 9 pièces.
Avec les dix fragments issus de cinq carrés découpés comme le carré central partagé en trapèze et triangle rectangle, on reconstitue le grand carré.
Figure interactive dans GeoGebraTube : carré d'aire cinq fois plus petite - 10 pièces
6. Multiplication par cinq de l'aire d'un carré
Rotation hors programme
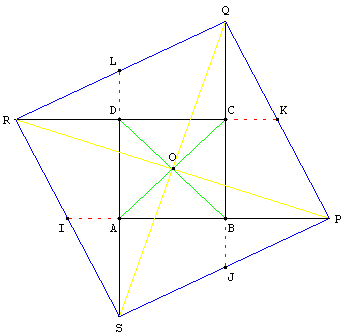
6.a. ABCD est un carré, P est le symétrique de A par rapport à B, Q est le symétrique de B par rapport à C, R est le symétrique de C par rapport à D et S est le symétrique de D par rapport à A.
Montrer que PQRS est un carré d'aire cinq fois plus grande.
La rotation de centre O et d'angle 90° transforme [AP] en [BQ], [BQ] en [CR]…
P a pour image Q, Q a pour image R, R a pour S et S a pour image P. Le quadrilatère PQRS globalement invariant par la rotation a ses quatre côtés de même longueur, deux côtés consécutifs forment un angle de 90°, égal à l'angle de la rotation. ADCD est un carré.
Si le côté du petit carré AB = a, la propriété de Pythagore dans le triangle BPQ permet de calculer PQ = a
. PQRS a une aire égale à 5a2.
Télécharger la figure GéoPlan mul_carres.g2w
