Descartes et les Mathématiques

L'espace en sixième
avec GeoGebra 3D

Parallélépipède rectangle : patrons.

Sommaire

1. Cube : perspective cavalière

2. Parallélépipède rectangle

3. Patron d'un parallélépipède rectangle

Technique GeoGebra : patron d'un polyèdre

1. Le cube : perspective cavalière

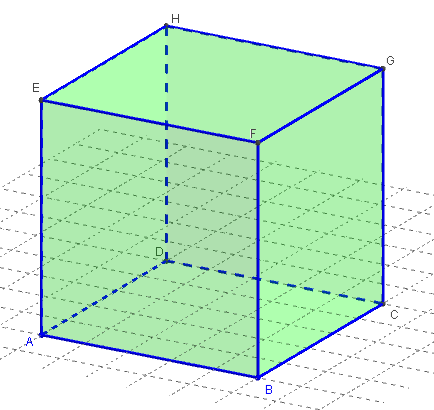
Le cube dans GeoGebra est défini par deux points
et le plan (xOy) ou une direction;
Il fallait y penser !

Il est possible de faire tourner la figure.

a³ est le volume du cube de côté a

Volume(ABCDEFGH)
    = Aire de la base × hauteur
    = Aire(ABCD) × AE
    = a² × a = a³.

Figures 3D dans GeoGebraTube : cube,

cube sur grille,

cube en fil de fer

Opacité

Dans les propriétés
du cube, choisir l'onglet
couleur et règler l'opacité à 25,

- choisir 0 pour une figure en fil de fer,
- 100 pour une figure opaque.

2. Parallélépipède rectangle

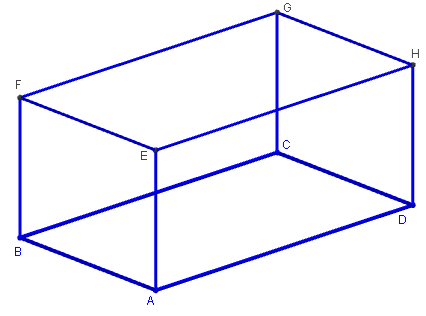
Définition du parallélépipède

Parallélépipède : polyèdre à six faces qui sont toutes
des parallélogrammes.
Les faces opposées sont égales et parallèles.
Parallélépipède rectangle : polyèdre à six faces
qui sont toutes des rectangles.

À l'école, le terme parallélépipède rectangle n'est pas
exigible au cycle 2, on lui préférera celui de pavé droit.

Volume du parallélépipède rectangle

AB = a, AD = b et AE = c.

Volume(ABCDEFGH)
    = Aire de la base × hauteur
    = Aire(ABCD) × AE = AB × AD × AE
    = a × b × c.

Commandes GeoGebra

La figure en fil de fer est obtenue en choisissant
0 comme coefficient d'opacité.

Modifier les mesures des côtés.
Décocher la case pour effacer les diagonales.

Figure 3D dans GeoGebraTube : pavé droit

Les diagonales sont concourantes en leur milieu

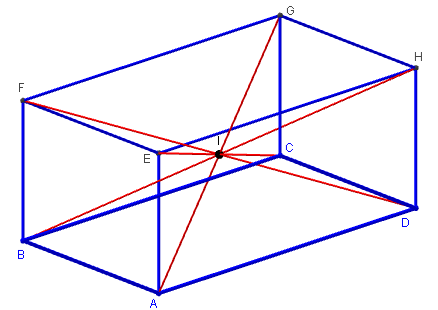
Par exemple, les diagonales [AG] et [EC] sont les
diagonales du rectangle ACGE.
Elles se coupent en leur milieu I.

Longueur d'une diagonale du pavé droit

Classe de quatrième

Pour calculer la longueur AG, utiliser le
théorème de Pythagore dans deux plans différents :
dans le triangle rectangle ABC, AC² = a² + b²,
dans le triangle rectangle ACG,
AG² = AC² + CG² = (a² + b²) + c².

La longueur de la diagonale est donnée
par AG² = a² + b² + c².

Figure 3D dans GeoGebraTube :
    diagonales du parallélépipède rectangle

Cas particulier :
longueur d'une diagonale du carré de côté a

dans le triangle rectangle isocèle ABC,
AC² = a² + a² = 2a²,
dans le triangle rectangle ACG,
AD² = AC² + CG² = (2a²) + a² = 3a².

La longueur de la diagonale du cube est AG = a

3. Patron d'un parallélépipède rectangle

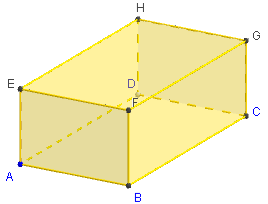
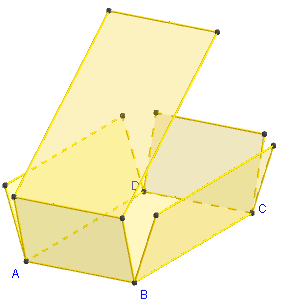
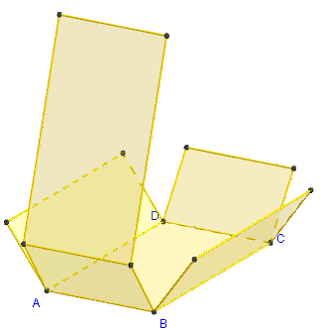
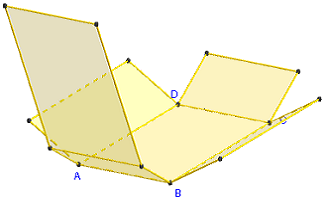
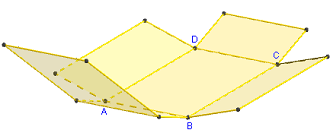
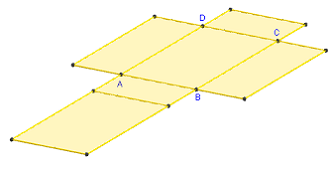
Commandes GeoGebra

Le patron est pilotable en faisant varier
le coefficient d'ouverture m de 0 vers 1.

Figure 3D dans GeoGebraTube :
     patron du pavé droit

Technique GeoGebra : patron d'un polyèdre

On obtient, parmi tous les patrons possibles,
un patron choisi par le logiciel à partir de la
face principale ayant servi à sa construction..
Les autres faces s'articulent autour de cette face.

Abus de langage de Google

Patron d'un rectangle : patron d'un parallélépipède
rectangle de base rectangulaire,
Patron d'un triangle : patron d'un prisme de base
triangulaire.

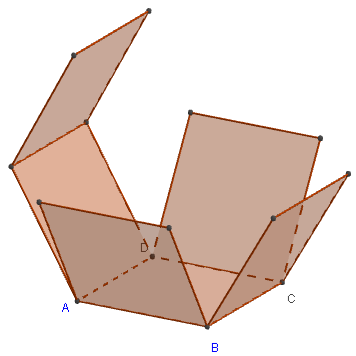
Classe de sixième – Patron de cube

Figure 3D dans GeoGebraTube : patron du cube

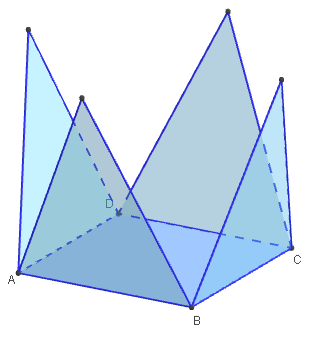
Classe de quatrième - Patron de pyramide

Figures 3D dans GeoGebraTube :
    pyramide de base carrée,
    patron de pyramide de base carrée

Le coefficient d'ouverture du patron est une variable
réelle m, comprise entre 0 et 1 ;
si elle est égale à 1 le patron est plan,
si elle est égale à 0 le patron coïncide avec le polyèdre.

Table des matières

…Avec GeoGebra 3D dans d'autres pages du site

Mode d'emploi GeoGebra 3D

GeoGebra 3D en 5^e : Prisme

GeoGebra 3D en 4^e : Pyramide

GeoGebra 3D en 3^e : Sections planes

Mobile friendly :
sur ordinateur, cette page pour grand écran

Page n^o 84, adaptée à GeoGebra 3D le 10/10/2014
adaptée aux mobiles le 9/12/2015