Descartes et les Mathématiques
Mode d'emploi GeoGebra 3D
Journée régionale APMEP - Grenoble – 4 mars 2015
Atelier n°2 : GeoGebra 3D - Animateur : Patrice Debart.
Après une présentation de GeoGebra 3D, nous explorerons quelques fonctionnalités du logiciel à travers deux exercices : section plane d’un tétraèdre déterminée par trois points et recherche du volume minimal d’une pyramide contenant un cube.
Vous pouvez apporter votre ordinateur portable ou votre tablette. Il est également possible de sauvegarder vos travaux sur GeoGebraTube.
NOEL Jean François- 20 février 2015
Sommaire
I. Premiers pas dans l'espace
Logiciel gratuit de géométrie dans l’espace
GeoGebra permet de créer, représenter et voir sous différents angles des figures de l'espace. Celles-ci sont composées d'objets divers fixes ou variables : points, droites, plans, polygones…
Il intègre également la possibilité de créer et manipuler vecteurs, transformations, variables numériques, fonctions, etc.
I. Premiers pas dans l'espace : ne pas se noyer dans l'aquarium
Fenêtres 2D et 3D
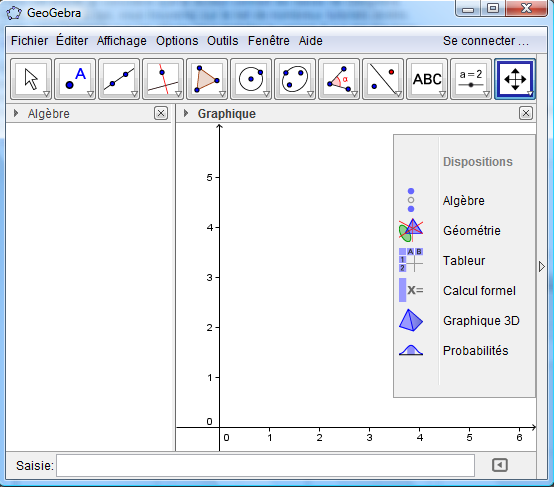
Au lancement de GGB, nous obtenons classiquement les deux fenêtres algèbre et graphique (2D).
Ajoutons, à l’aide du menu Affichage, la fenêtre Graphique 3D.
Tout objet graphique créé sera inséré automatiquement dans la fenêtre 3D.
S'il y a lieu, la partie de l'objet située dans le plan (xOy) sera affichée dans la fenêtre graphique (2D).
Il y a alors automatiquement, dans la fenêtre algébrique, l'expression de l'objet avec trois coordonnées.
De même un objet, créé dans la fenêtre graphique 2D, sera inséré dans le plan horizontal du graphique 3D et son expression, avec deux coordonnées, insérée dans la fenêtre algébrique.
Avec la ligne de saisie, il est aussi possible de créer une expression qui sera insérée dans la fenêtre algébrique et qui créera un objet géométrique dans la fenêtre 3D et éventuellement dans la fenêtre 2D.
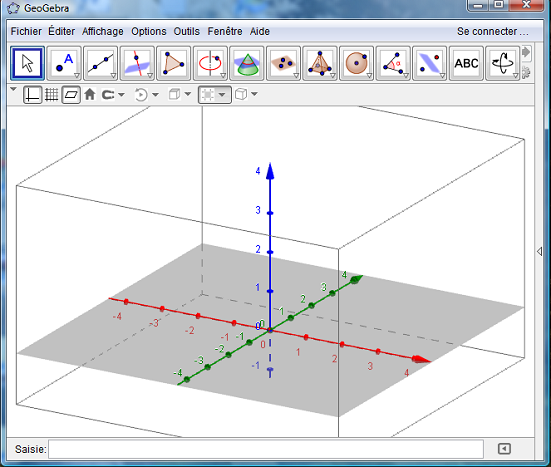
La fenêtre 3D contient une « boîte de visualisation » avec un repère 3D gradué.
C'est « l'aquarium » de diagonales Coin[-1,1] ; Coin[-1,3] en bas et Coin[-1,5] ; Coin|-1,7] en haut.
Le plan (xOy) y est grisé.
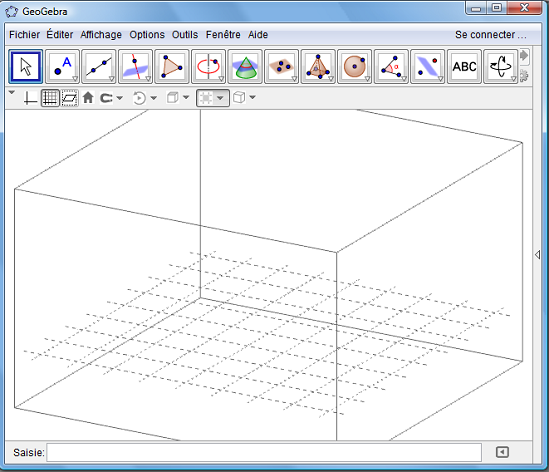
Utiliser la barre de style pour effacer les axes, faire apparaître la grille ou effacer le plan (xOy).
Pour effacer les contours de la « boîte de visualisation », cliquer sur l'icône « espace restreint ».
Clarifier la fenêtre 3D
Pointer dans la fenêtre 3D ; activer le menu écran en cliquant sur l'icône rotation.
Cliquer en dessous sur le bandeau 
pour faire apparaître la barre de style sur la figure de droite.
Ci-dessus à droite ; utiliser la barre de style pour effacer les axes, faire apparaître la grille ou effacer le plan (xOy)
Il est conseillé de sauver cette figure vierge, puis la reprendre pour commencer un nouveau travail.
Une seule figure avec deux zones
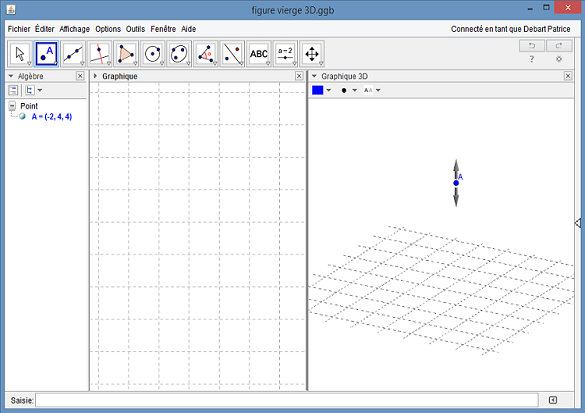
Le plan (xOy) est le plan de la figure 2D visualisable dans une fenêtre graphique. Toute construction d’un objet dans la fenêtre 2D fera apparaître l’objet dans la fenêtre 3D, et réciproquement.
Placer un point dans l'espace
Maîtriser le déplacement de la flèche de sélection : horizontal dans le plan xOy ou vertical dans l’espace.
On ne peut placer un point directement dans l'espace : il faut promener la souris dans le plan horizontal, puis à partir de la croix, monter le point dans l'espace avec la double flèche vertical.
Réorganisation des fenêtres graphiques 2D et 3D
Déplacement des fenêtres graphiques
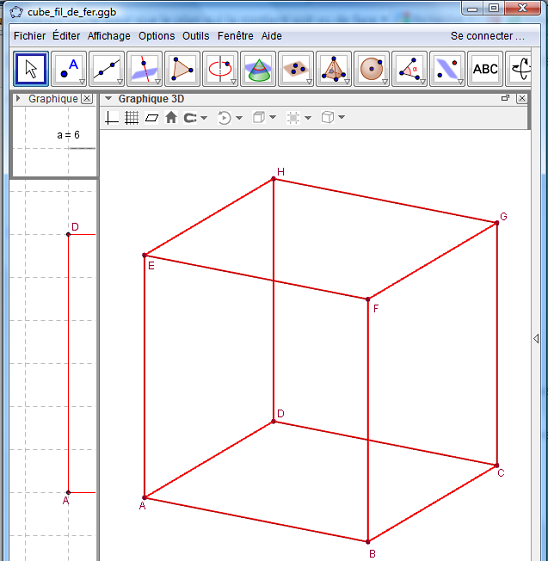
Fenêtre 3D au-dessus de la fenêtre 2D
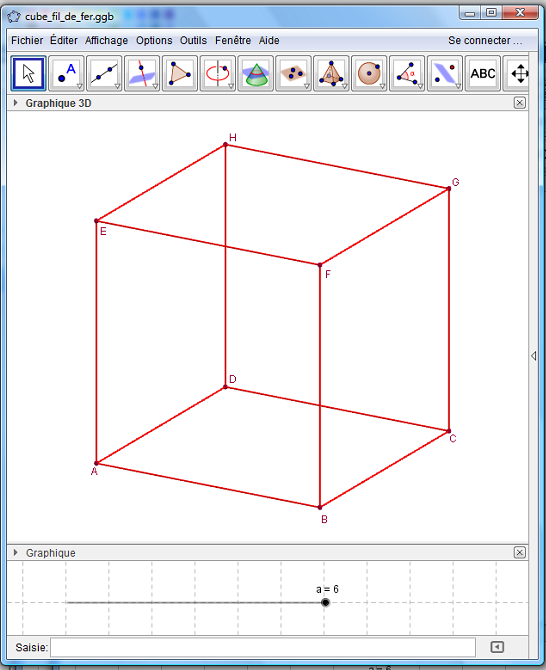
Par défaut les fenêtres graphiques partagent l'écran verticalement.
Pour utiliser ces deux fenêtres l'une en dessous de l'autre, il suffit de déplacer la barre de séparation le plus à gauche possible.
Maintenir le clic sur la ligne et en se déplaçant sur la gauche : un rectangle apparaît en haut de l'écran.
Il suffit de relâcher pour que le graphique 3D passe en haut de l'écran.
En travaillant les tailles des fenêtres, on obtient l'écran ci-dessus à droite.
Figure 3D dans GeoGebraTube : cube en fil de fer
Création d'objets 3D à l'aide d'outils
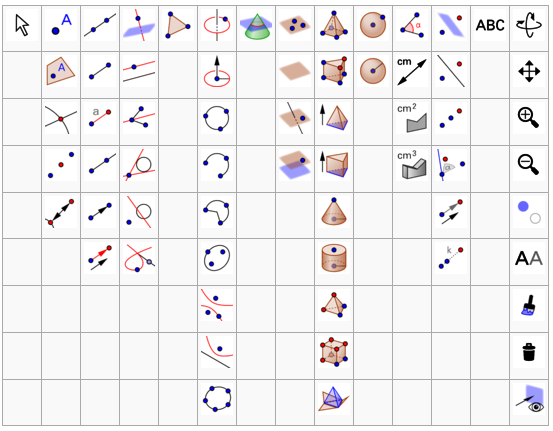
Les outils des quatre colonnes de gauche sont identiques à ceux du plan.
Pour les transformations, on n’a toujours pas la projection.
Pour projeter,
utiliser :
- le point d’intersection de l’axe avec une perpendiculaire,
- ou le milieu entre un point et son symétrique.
On n’ a pas plus la similitude : composer homothétie et rotation.
Outils utilisables uniquement dans la fenêtre graphique
Curseur
Il est aussi possible de saisir la variable a = 2
puis l'afficher et régler les propriétés
Boite de sélection des objets
Après une construction, on a souvent envie de gommer les traits intermédiaires.
L'utilisation de cette icône est assez fastidieuse.
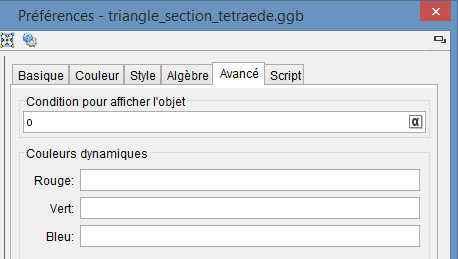
Je préfère créer un booléen o= false, l'afficher.
Dans le menu propriété, onglet avancé, sélectionner tous objets et y entrer manuellement le nom o du booléen dans le champ de visibilité conditionnelle.
Comme o est à false, les objets disparaissent, ce qui permet de savoir où en est.
Outils polyèdre
La construction des principaux polyèdres y est possible et le logiciel gère correctement les arêtes et les faces cachées. Les Outils 3D permettent de construire :
Extrusion pyramide/cône
Extrusion prisme /cylindre
cône
cylindre
Cube
et leurs patrons à partir de la base située dans le plan horizontal.
D’autres outils permettent la représentation des sphères de rayon donné ou passant par un point.
Avec la ligne de saisie, Il aussi possible de construire dodécaèdre, icosaèdre et octaèdre.
Comme tout les polyèdre il suffit de choisir deux points A et B dans le plan horizontal et de saisir poly=Polyèdre[A,B]
Outils pouvant poser problème
Outils droite perpendiculaire
En cas difficulté, saisir en bas de l'écran :
d=Perpendiculaire[M, axeX,axeY] pour une perpendiculaire en M au PlanxOy.
Dès que l'on tape d=pe le logiciel propose la syntaxe précise :
d=Perpendiculaire[<Point>, <Plan>]
Outils intersection de surfaces
Pour l'intersection d'un plan et d'un polyèdre, avec la souris, il n'est pas facile de sélectionner tout le polyèdre et souvent on ne sélectionne qu'une seule face.
On a intérêt à montrer le plan, puis dans le menu algèbre, sélectionner Poly ;
ou bien, en bas de l'écran, saisir d=IntersectionChemins[Plan[A,B,C], Poly]
Dès que l'on tape d=Int le logiciel propose la syntaxe précise :
d=IntersectionChemins[ <Plan>, <Polygone> ]
Remplacer les <...> par le nom du plan et celui du polyèdre.
Étiquetage des nouveaux points
Cette option évite d'afficher les noms des objets et des droites secondaires crées.
Barre de style
GeoGebra pour Ordinateurs
Pour visualiser la barre de style, cliquer sur le bouton ‘Bascule Barre de style' à gauche du titre dans le bandeau supérieur de la fenêtre.
GeoGebra pour Tablettes ou Tube
Cliquer sur l'icône 3G 
dans le coin supérieur droit de la fenêtre Graphique 3D.
.La barre de style se développe vers la gauche, un autre clic efface le menu.
Afficher/cacher les axes, la grille, le PlanxOy ;
Maison (home) : retour (aléatoire) à la vue standard ;
Aimant : capture d’un point ;
Flèche circulaire : démarrer/arrêter la rotation autour d'un 'axe parallèle à axeZ.
Espace restreint : petit, moyen, grand ;
Engrenage : dialogue propriété pour les objets de la figure ;
Trois carrés verticaux : affichage de nouvelles fenêtres.
II. Section déterminée par trois points sur un tétraèdre
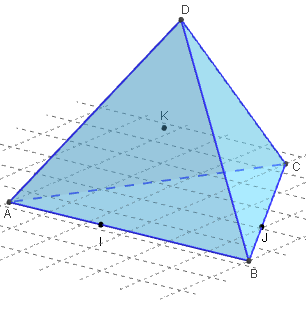
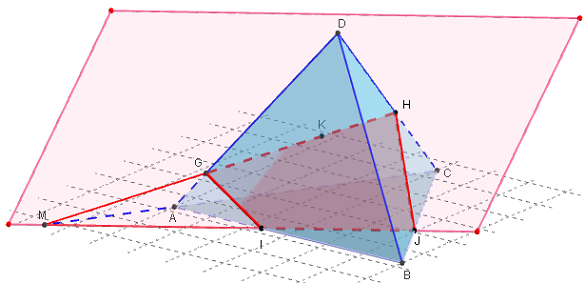
ABCD est un tétraèdre. I et J sont deux points sur les arêtes [AB] et [BC] ; K est un point sur la face ACD ne contenant pas les points I et J. - Étudier la section plane du tétraèdre par le plan (IJK).
1) Tracer la section plane avec GeoGebra
2) Construire l'intersection du plan avec les faces du tétraèdre.
Avec GeoGebra
Charger la figure de figure de base de GeoGebraTube : Trois points sur un tétraèdre
Dans GeoGebra : Fichier > ouvrir depuis GeoGebraTube > rechercher Trois points sur un tétraèdre
ou avec un navigateur : https://www.geogebra.org/m/CvlxGcbD - Figures ci- dessous : Correction
Construction du point K
Saisie K=point[ACD]
ou faire une rotation pour placer le plan (ACD) de face, et y placer le point K ;
ou encore cacher les faces ABD, BCD; placer K, puis réafficher les deux faces.
1) Section plane d’un tétraèdre – figure dynamique
Tracer la section plane avec l’outil GeoGebra intersection de surface,
ou avec la saisie de la commande IntersectionChemins[ <Plan>, <Solide> ]
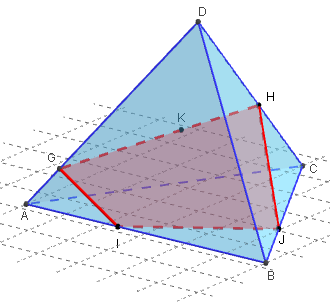
L'intersection du plan (IJK) avec les faces du tétraèdre ABCD est un quadrilatère IJHG.
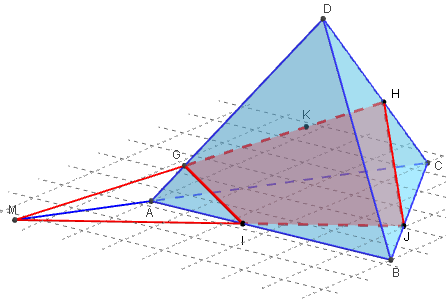
2) Construction l'intersection du plan avec les faces du tétraèdre.
Construction géométrique, en utilisant le point M d'intersection de l'arête (AC) avec la droite (IJ). Les intersections la droite (MK) avec les côtés du tétraèdre permet de trouver les deux autres sommets de la section.
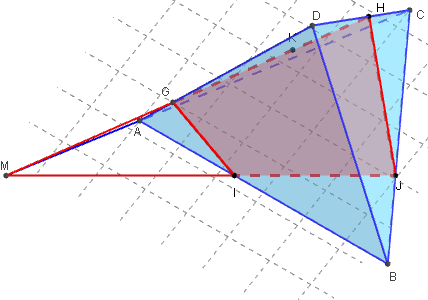
Vue de face : Sélectionnez la section plane pour que le plan qui la contient soit vu de face, le quadrilatère apparaît en vraie grandeur.
III. Cube dans pyramide
Un fabricant veut commercialiser un produit qui a la forme d'un cube, dans un emballage qui a la forme d'une pyramide régulière à base carrée.
Le but du problème est de trouver les dimensions d’une pyramide de volume minimal contenant un cube.
Variantes
- pyramide de surface minimale
- pyramide dont le patron est inscrit dans une feuille carrée de taille minimale.
Avec GeoGebra, charger la figure de base dans GeoGebraTube : cube sur carré
ou dans le logiciel, choisir : Fichier > ouvrir depuis GeoGebraTube > rechercher : cube sur carré
Volume minimal d'une pyramide contenant un cube
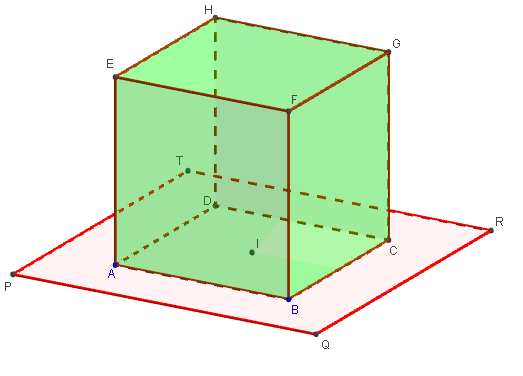
Le cube posé sur le PlanxOy a pour trace, dans ce plan, le carré ABCD.
Dans ce même plan le carré PQRT, de côté x1, a même centre I et leurs côtés sont deux à deux parallèles.
Figure ci-contre
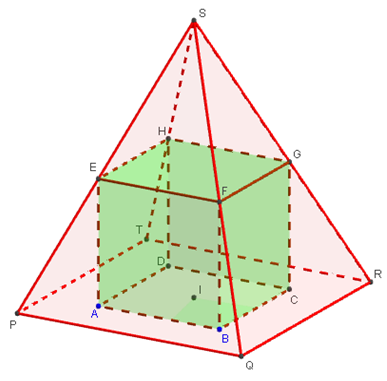
On a construit le sommet S d'une pyramide PQRTS contenant les sommets E, F, G et H du cube.
Figure ci-dessous
On a déplacé la fenêtre 3D pour faire apparaître dans la fenêtre graphique le repère vierge xOy.
Si v est le volume de la pyramide (commande v = volume[<solide>] ), dans la fenêtre graphique, placer le point M(x1, v) dont on garde la trace.
(J’appelle la variable x1, car les noms x, y et z sont réservés par le système)
Volume minimal d'une pyramide régulière à base carrée contenant un cube
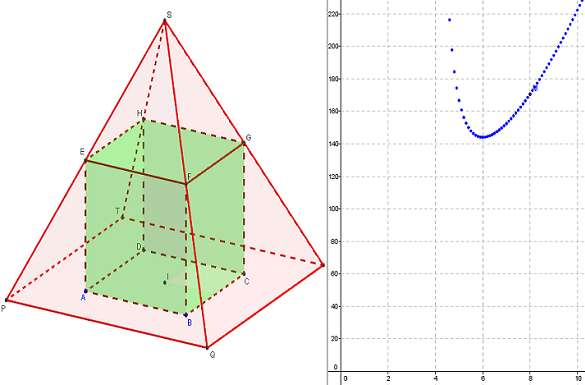
On obtient le minimum pour x = 6.
GeoGebraTube
Commandes script
SoitValeur : voir le script par actualisation d'une case à cocher, pour afficher un tétraèdre régulier.
En projet
Table des matières
…Avec GeoGebra 3D dans d'autres pages du site
Technique GeoGebra 3D : patron d'un polyèdre
4e Pyramide
2nde Incidence et cube
2de Tétraèdre
Sections de cube en 1S
Géométrie plane …avec GeoGebra 2D
Google friendly
Page no 204, créée le 7/3/2015