Descartes et les Mathématiques
Polyèdres avec GeoGebra 3D
Ancienne version GéoSpace, adaptation à GeoGebra en cours.
Les cinq solides de Platon : tétraèdre, cube, octaèdre, dodécaèdre, icosaèdre ; et sept autres solides archimédiens.
Sommaire
1. Prisme de base triangulaire
2. Prisme dont la base est un parallélogramme
3. Cube
4. Une maison avec GeoGebra 3D
5. Cube tronqué
6. Tétraèdre
7. Pyramide
Solides de Platon
8. Octaèdre
9. Dodécaèdre
10. Icosaèdre
11. Dualité – Cinq solides de Platon
Solides d'Archimède
12. Rhombododecaèdre
13. Cuboctaèdre
1. Prisme
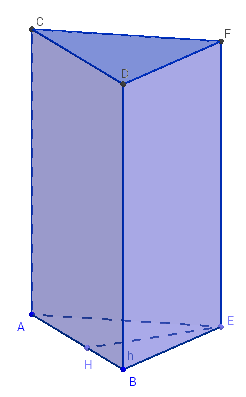
Un prisme est un solide ayant deux bases qui sont des polygones. Ces polygones situés dans des plans parallèles sont isométriques.
Les arêtes du prisme sont des droites parallèles. Les faces latérales sont des parallélogrammes.
Pour un prisme droit, les arêtes sont perpendiculaires aux plans des bases et les faces latérales sont des rectangles.
Leur longueur est alors la hauteur du prisme, égale à la distance entre les deux bases.
Figures 3D dans GeoGebraTube : prisme vertical de base triangulaire, prisme horizontal de base triangulaire
Volume d'un prisme droit : Aire de la base × hauteur = B × h.
2. Parallélépipède rectangle
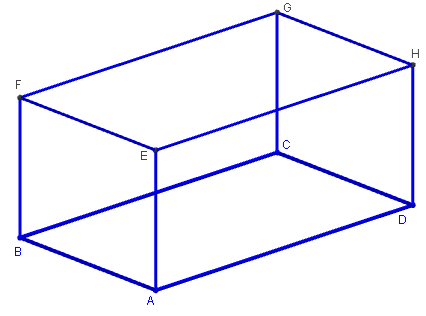
Définitions
Parallélépipède : polyèdre à six faces qui sont des parallélogrammes. Les faces opposées sont égales et parallèles.
C'est un prisme dont la base est un parallélogramme.
Parallélépipède rectangle : polyèdre à six faces rectangulaires. C'est un prisme droit dont la base est un rectangle.
Figure 3D dans GeoGebraTube : pavé droit
Volume du parallélépipède rectangle
Volume(ABCDEFGH) = Aire de la base × hauteur
= Aire(ABCD) × AE = AB × AD × AE.
3. Cube
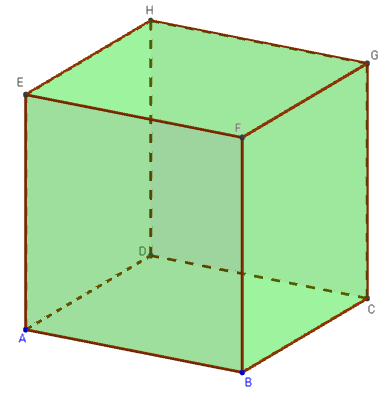
Le cube est un solide de Platon.
Volume du cube de côté a : V = a3.
Figures 3D dans GeoGebraTube : cube, cube en fil de fer
4. Une maison avec GeoGebra 3D
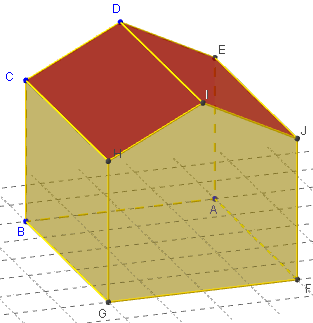
La reproduction d'une maison a la forme d'un parallélépipède rectangle, surmonté d'un prisme droit.
La longueur du parallélépipède est de 7 cm, sa largeur de 5 cm et sa hauteur de 4 cm.
La hauteur totale de cette maison est de 6 cm.
Le volume v est alors de 175 cm3.
Figure 3D dans GeoGebraTube : maison
5. Cube coupé ou tronqué
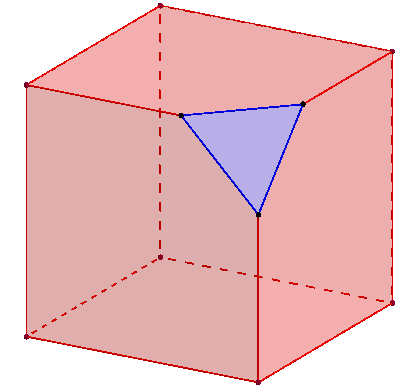
Cube aux « coins coupés » ; cube aux « angles coupés ».
Rallye Mathématiques Poitou-Charentes - 2007
Cube coupé
Solide à 7 faces.
On a coupé un « coin » du cube au tiers des arêtes par un plan perpendiculaire à une diagonale du cube.
Représenter en perspective le solide obtenu en coupant, de même manière, les huit « coins » : cf. figure ci-contre à droite.
Figures 3D dans GeoGebraTube : cube au coin coupé, cube au coin coupé opaque
Voir : « coin du cube » ; « cube fortement tronqué » lorsque les côtés du « cube coupé » sont trois des diagonales faces du cube.
Voir aussi les arts conceptuels de Sol LeWitt : wall drawings
Cube aux huit « coins coupés »
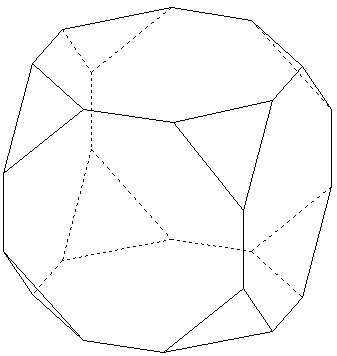
Les côtés des triangles sont de longueur inférieure à la moitié de la longueur d'une diagonale d'une des faces du cube.
Polyèdre a 14 faces : 8 triangles équilatéraux et 6 octogones, 24 sommets et 36 arêtes.
Ce solide est un cube tronqué ou hexaèdre tronqué lorsque les faces octogonales sont régulières.
Le cube tronqué est un des 13 solides d'Archimède.
Télécharger la figure GéoSpace cube_tronque.g3w
Voir aussi : cuboctaèdre
6. Tétraèdre régulier
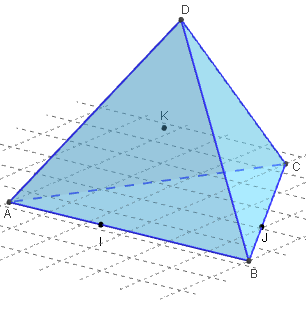
Le tétraèdre régulier est un des cinq solides de Platon.
Les quatre faces sont des triangles équilatéraux.
Toutes les arêtes sont de même longueur.
Les quatre hauteurs sont aussi des médianes, concourantes au centre de gravité.
Un tétraèdre régulier est orthocentrique.
Figures 3D dans GeoGebraTube : tétraèdre régulier
Tronc de tétraèdre
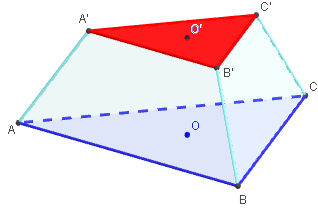
Le tronc de tétraèdre est un solide à 5 faces.
Figure 3D dans GeoGebraTube : section plane et tronc d'un tétraèdre
Tétraèdre tronqué
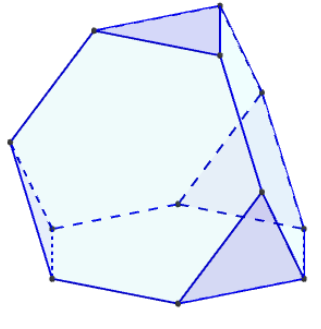
Polyèdre a 8 faces : 4 triangles et 4 Hexagones, 12 sommets et 18 arêtes.
Le tétraèdre tronqué est un des 13 solides d'Archimède.
Figures 3D dans GeoGebraTube : tétraèdre tronqué
7. Pyramide
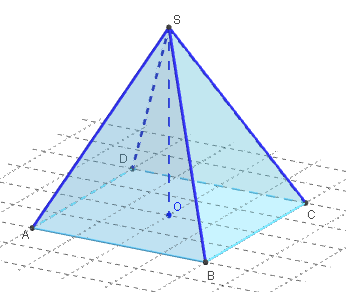
Le volume de la pyramide est :
V = 
× Sbase × hauteur, où Sbase est l'aire de la base ABCD et où la hauteur est la distance de S à la base.
Figure 3D dans GeoGebraTube : pyramide de base carrée
Pyramide de Khéops : nombre d'or
Tronc de pyramide
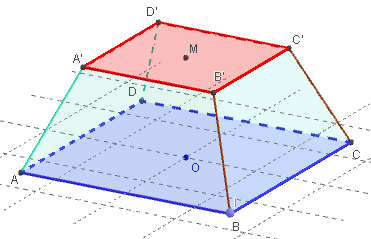
En appelant B l'aire de la grande base ABCD, b l'aire de la petite base A’B’C’D’et h la hauteur du tronc, le volume du tronc de pyramide est alors :
V = 
[B + b + 
].
Figure 3D dans GeoGebraTube : section plane et tronc d'une pyramide de base carrée
Lanterne - solide composite
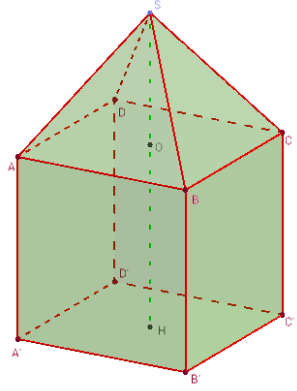
Solide composite formé par un cube, coiffé par une pyramide
Figure 3D dans GeoGebraTube : lanterne
Les cinq solides de Platon
Décrire les solides obtenus : nombre de faces, nombre d'arêtes, nombre de sommets.
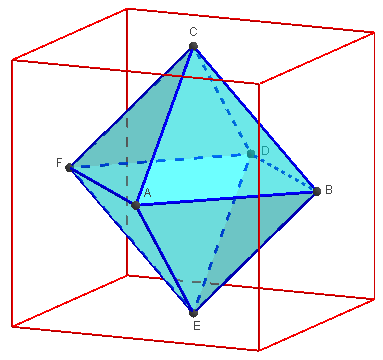
8. Octaèdre régulier
Avec deux points A et B dans le plan de base PlanxOy, tels que AB = a,
l'instruction poly=Octaèdre[A, B] crée dans la fenêtre graphique un point C à une distance égale à a
de [AB], puis un triangle équilatéral ABC.
Le polyèdre Octaèdre[A, B, C] est développé dans la fenêtre 3D.
Les huit faces de l''octaèdre sont des triangles équilatéraux.
6 sommets et 12 arêtes de même longueur a.
L'octaèdre est formé de deux pyramides (bipyramide) de base carrée, dont les faces latérales sont des triangles équilatéraux.
La hauteur de chacune des pyramides est égale à la moitié de la longueur de la diagonale de la base a
.
L'octaèdre est un des cinq solides platoniciens.
Commande GeoGebra 3D
polyedre=Octaèdre[A, B]
Figure 3D dans GeoGebraTube : octaèdre
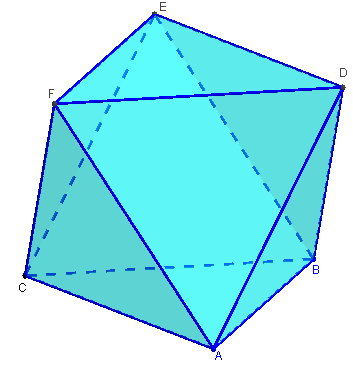
Octaèdre d'axe vertical
Avec deux points A et B tels que AB = a, il est possible de tracer un triangle équilatéral de côté a en plaçant un point C sur le cercle de centre I milieu de [AB], d'axe (AB) et de rayon a .
Pour un octaèdre ABCDEF, d'axe [CD] vertical, le carré ABEF de centre O est horizontal.
Le point C est alors à l'intersection du cercle et de la verticale passant par O.
L'instruction poly=Octaèdre[A, B, C] développe le polyèdre.
Figure 3D dans GeoGebraTube : octaèdre d'axe vertical
Figure copiée par pinterest : Bipyramide de base carrée
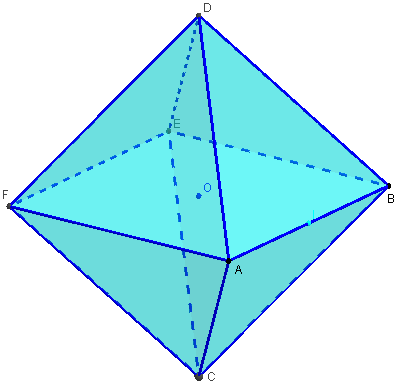
Octaèdre inscrit dans un cube
On peut construire un octaèdre régulier en prenant pour sommets les six centres des faces d'un cube.
L'octaèdre est formé de deux pyramides (bipyramide), de base un carré situé dans un plan médiateur du cube.
Les faces latérales sont des triangles équilatéraux.
Les diagonales de l'octaèdre ont pour longueur le côté c du carré.
Les côtés de l'octaèdre mesurent c
.
Figure 3D dans GeoGebraTube : octaèdre inscrit dans un cube
Octaèdre inscrit dans un tétraèdre régulier
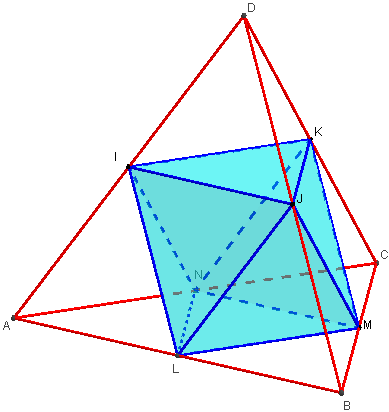
Soit ABCD un tétraèdre régulier (toutes les arêtes ont la même longueur).
Pour chaque arête, on joint son milieu avec tous les milieux des arêtes qui ne lui sont pas opposées (par exemple [AB] et [CD] sont des arêtes opposées). Les segments sont situés sur les faces du tétraèdre.
La figure obtenue par cette construction est un octaèdre régulier.
Avec GeoGebra 3D
Si LMN est le triangle équilatéral médian de la face ABC, il suffit de saisir :
poly = Octaèdre[L, M, N]
Figure 3D dans GeoGebraTube : octaèdre inscrit dans un tétraèdre
Octaèdre tronqué
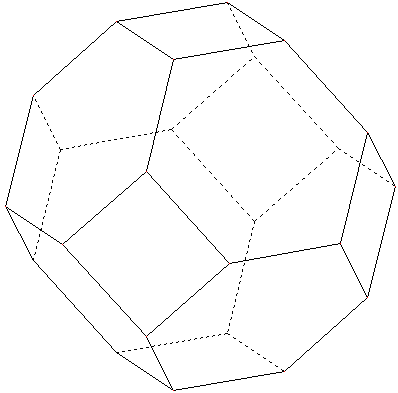
Solide d'Archimède ayant 14 faces : 8 faces hexagonales régulières, 6 faces carrées ; 24 sommets et 36 arêtes de même longueur.
Dual : tétrakihexaèdre
Octaèdre et octaèdre tronqué
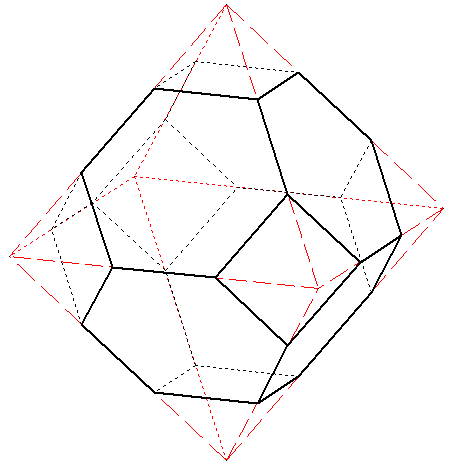
Télécharger la figure GéoSpace octaedre_tronque.g3w
Commande
Afficher/effacer l'octaèdre.
Polyèdre de Lord Kelvin
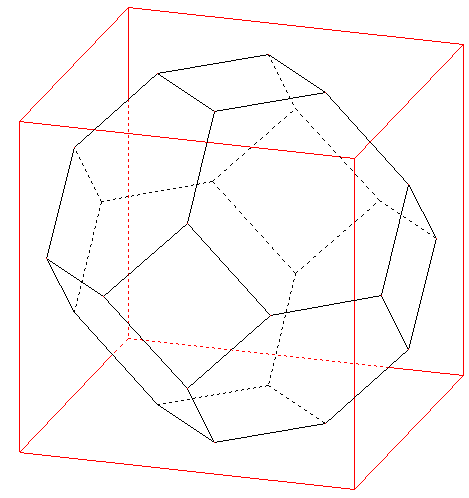
Octaèdre tronqué inscrit dans un cube
À l'intérieur d'un cube, on construit le polyèdre de Lord Kelvin : ses sommets sont les milieux des segments obtenus en joignant les centres des faces aux milieux des arêtes.
Télécharger la figure GéoSpace Lord_kelvin.g3w
Commande
afficher/effacer le cube
9. Dodécaèdre
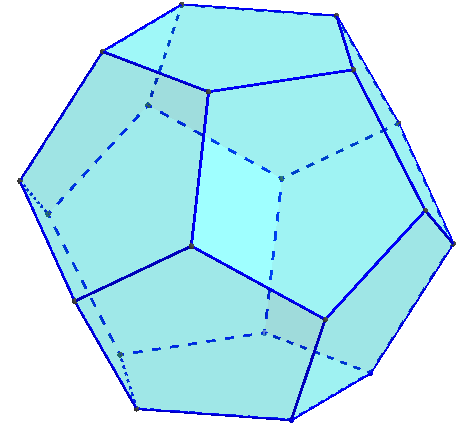
Dodécaèdre régulier
Douze faces pentagonales, vingt sommets et trente arêtes de même longueur.
Avec deux points A et B dans le plan de base PlanxOy,
l'instruction poly=Dodécaèdre[A, B] crée dans la fenêtre graphique un point C.
Le polyèdre Dodécaèdre[A, B, C] est développé dans la fenêtre 3D.
Longtemps le nombre cinq et le nombre d'or furent des objets fétiches, associes au dodécaèdre de Platon.
Il en est reste le mot quintessence.
Figure 3D dans GeoGebraTube : dodécaèdre
Figure copiée par pinterest : dodécaèdre
Patron d'un demi-dodécaèdre
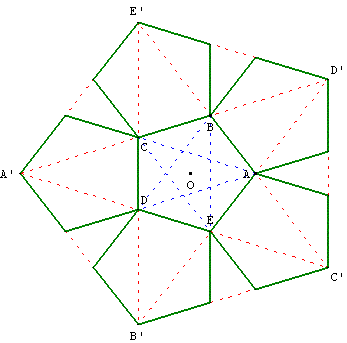
Dodécaèdre à plat
Former un grand pentagone avec six petits pentagones
Télécharger la figure GéoPlan dodecaedre_patron.g2w
Quinse polyèdres : Patron d'un demi-dodécaèdre
Image dupliquée par pinterest
pinterest
pinterest
pinterest
Dodécaèdre, jardin Bellini Catane Sicile
Construction du dodécaèdre par pliage de bandes de papier
Pour la construction du dodécaèdre, il faut réaliser 12 pièces identiques composées d'un pentagone régulier et de deux languettes.
Une construction exacte, mais un peu délicate, consiste à faire un nœud simple avec douze bandes de papier de même largeur.
Tirer sur les extrémités afin de mettre à plat le nœud et plier les bandes qui dépassent pour former les deux languettes.
Dodécaèdre tronqué
Il est possible de tronquer le dodécaèdre en transformant les pentagones en 12 décagones réguliers, en coupant par 20 triangles équilatéraux. On obtient 60 sommets et 90 arêtes.
10. Icosaèdre
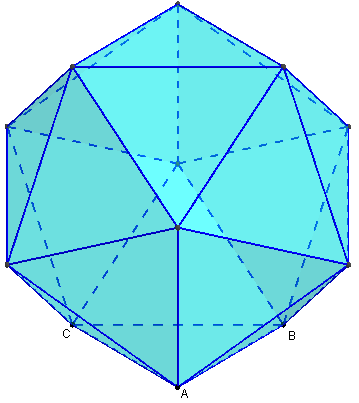
Vingt faces, douze sommets.
Avec deux points A et B dans le PlanxOy,
l'instruction poly=Icosaèdre[A, B] crée dans la fenêtre graphique un point C.
Icosaèdre[A, B, C] est développé dans la fenêtre 3D.
Figure 3D dans GeoGebraTube : icosaèdre
Skwish de Manhattan toy
Pour des raisons techniques, afin de n'utiliser qu'un seul fil élastique, il manque les arêtes reliant les sommets situés sur les diagonales parallèles.
Télécharger la figure GéoSpace skwish.g3w
Skwish
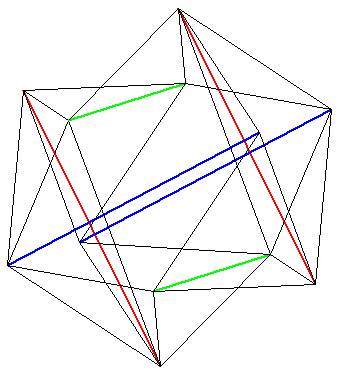
Le hochet ci-dessus est un icosaèdre avec des arêtes souples en élastique, 6 diagonales rigides, deux à deux parallèles, reliant les 12 sommets, il n'y a que quatre arêtes par sommet.
Le Skwish - Merveille du monde
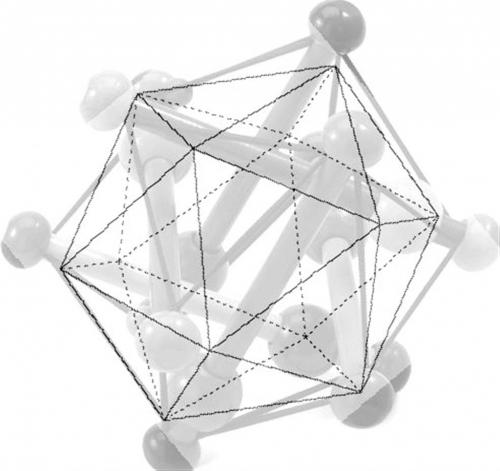
L'enfant est né. Les siens, généreux et touchés, l'accueillent avec le meilleur, avec le plus beau, avec le fleuron.
Ainsi, le Skwish : un ténor des cadeaux de naissance. Remarquable jouet à structure moléculaire, évocation quadrichromique du big bang et de corps célestes, le Skwish s'est hissé au rang de merveille du monde des jouets.
Le Skwish est sorti, dans les années 1980, de l'imagination de Tom Flemons, Canadien de la côte Ouest, sculpteur et designer. Un mordu acquis au principe de la tenségrité. Tenségrité : combinaison des mots tension et intégrité, traduisant la faculté d'une structure à se stabiliser par le jeu des forces de tension et de compression qui s'y répartissent et s'y équilibrent.
Le Skwish est un système mécanique, auquel Tom Flemons ajoutera des caractères géométriques.
Cinq solides de Platon
Depuis l'Antiquité, les solides de Platon fascinent.
11. Dualité
Le cube a six faces et huit sommets et l'octaèdre huit faces et six sommets.
En marquant les centres des faces d'un octaèdre régulier, nous obtenons un cube.
Cube et octaèdre sont en relation de dualité et cette relation est réciproque.
Le tétraèdre régulier, avec ses quatre faces, quatre sommets et six arêtes, est son propre dual.
Le dodécaèdre a 20 sommets et les 12 faces sont des pentagones réguliers.
L'icosaèdre a 12 sommets et les 20 faces sont des triangles équilatéraux.
Le dodécaèdre et l'icosaèdre sont duaux l'un de l'autre.
Platon, philosophe grec (428 à 348 avant J.-C.), est le premier à démontrer qu'il n'existe pas d'autres solides réguliers dont les faces sont des figures équiangles et équilatères que ces cinq polyèdres (sous-entendu solide convexe, avec même répartition des faces en chaque sommet).
Platon
Relation d'Euler ou théorème de Descartes-Euler
Pour un polyèdre convexe, on a la formule f + s = a + 2, où f est le nombre de faces, s le nombre de sommets et a le nombre d'arêtes.
Vérifier cette formule, énoncée par Descartes en 1639, sur les cinq solides de Platon, sur une « lanterne », sur le tétraèdre tronqué.
Voir : quatre relations d'Euler
La version de Descartes
Un article de WikiPédia
Dans un mémoire inédit, Descartes énonce le théorème suivant :
« L'angle droit étant pris pour unité, la somme des angles de toutes les faces d'un polyèdre convexe est égale à quatre fois le nombre de sommets diminué de 2 »
L'aspect du théorème semble fort éloigné de la relation d'Euler. Elle lui est portant rigoureusement équivalente et Descartes, dans les applications qu'il en fait, passe assez naturellement de cette forme à celle d'Euler.
Preuve de l'équivalence :
Il faut se servir de la propriété de la somme des angles d'un polygone convexe : si le polygone convexe a n côtés, la somme des angles vaut 2(n - 2) droits. La somme de tous les angles sur toutes les faces est donc 4a - 4f droits (en effet, la somme des nombres de côtés de chaque face donne deux fois le nombre d'arêtes).
L'égalité de Descartes s'écrit donc 4a - 4f = 2(s - 2). Rigoureusement équivalente à s + f = a + 2.
Solides d'Archimède
Les plus beaux polyèdres
Solide d'Archimède (287-212 avant J.-C.) : Polyèdre semi-régulier dont les faces sont des polygones réguliers, ceux-ci pouvant être différents, mais disposés dans le même ordre autour de chaque sommet.
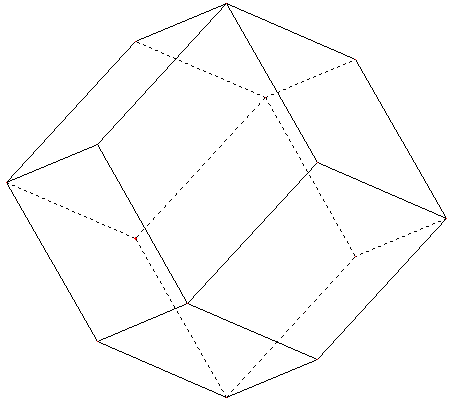
12. Rhombododecaèdre ou dodécaèdre rhombique
Polyèdre dont les douze faces sont des losanges identiques, mais assemblés par trois autour de certains sommets et par quatre autour de certains autres. (ce qui l'empêche d'être classé dans les polyèdres réguliers).
Télécharger la figure GéoSpace rhombododecaedre.g3w
On l'obtient à partir d'un cube :
on construit les symétriques du centre du cube par rapport à ses faces et on joint les quatorze points (les 8 sommets du cube, plus les 6 symétriques du centre).
En déduire le volume.
Commande
Afficher/effacer le Cube.
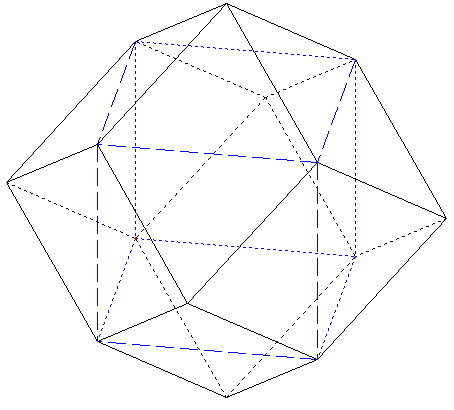
13. Cuboctaèdre
Solide ayant 14 faces : 6 carrés et 8 triangles équilatéraux ;
12 sommets ; 24 arêtes de même longueur, chacune commune à un triangle et un carré.
Télécharger la figure GéoSpace Cuboctaedre.g3w
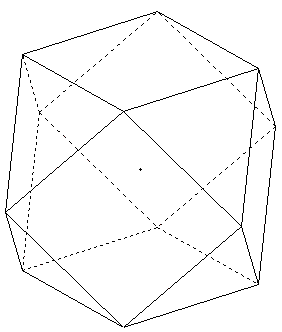
Cube fortement tronqué
On a coupé les huit « coins » du cube jusqu'aux milieux des arêtes.
Des faces ne subsistent que des carrés ayant pour sommets les milieux des arêtes.
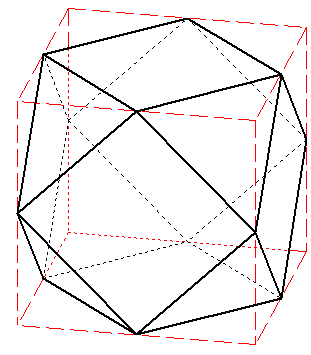
Octaèdre fortement tronqué
On a coupé les six « coins » d'un octaèdre jusqu'aux milieux des arêtes.
Ne subsistent des faces que des triangles équilatéraux ayant pour sommets les milieux des arêtes.
Cube et octaèdre tronqués
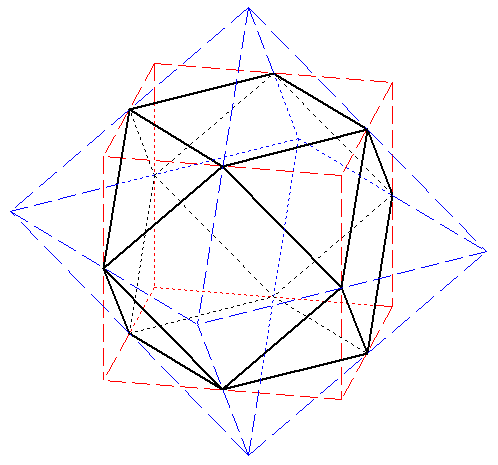
Télécharger la figure GéoSpace cube_octaedre.g3w
Commandes
afficher/effacer le Cube,
afficher/effacer l'octaèdre.
14. Le ballon de football - Icosaèdre tronqué
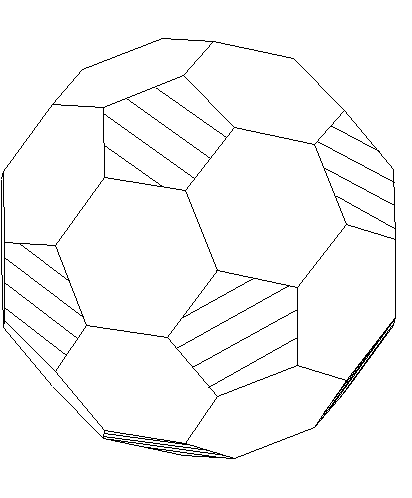
On coupe un icosaèdre au tiers de chaque arête, à partir des sommets.
32 faces : 12 pentagones, 20 hexagones, 60 sommets et 90 arêtes.
Copie twitter : t.co/NLqf5gIgOT
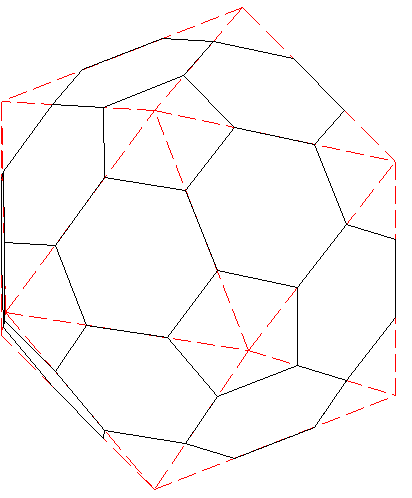
Commande
afficher/effacer l'icosaèdre.
Télécharger la figure GéoSpace ballon_football.g3w
15. Petit rhombicuboctaèdre
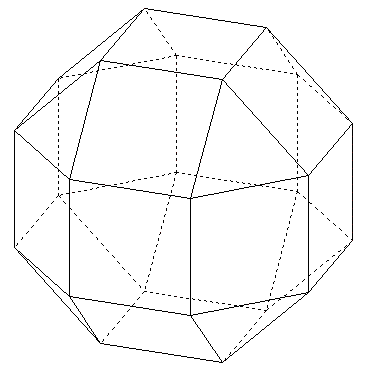
Télécharger la figure GéoSpace rhombicuboctaedre.g3w
Le petit rhombicuboctaèdre est un solide d'Archimède avec huit faces triangulaires et dix-huit faces carrées ; 24 sommets.
Les coordonnées des sommets sont toutes les permutations de
{±1 ; ±1 ; ±(1 + ) }.
Rhombicuboctaèdre de Vinci
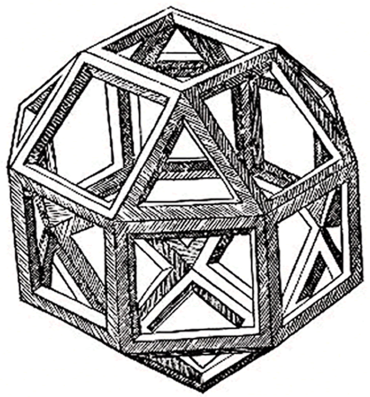
Première version imprimée d'un petit rhombicuboctaèdre, par Léonard de Vinci qui apparaît dans la Divine Proportion de Luca Pacioli (Venise, 1509)
Table des matièresDans d'autres pages du site Tétraèdre Tétraèdre tronqué d'Achichimède Tétraèdre orthocentrique : tétraèdre en seconde
Cube Coin de cube et sections planes : cube en seconde |
Pyramide Partition d'un cube en trois ou six pyramides Sections planes de pyramide
|
|
studylibfr.com/polyèdres---descartes-et-les-mathématiques Copyright 2007 - © Patrice Debart | |
|
Page no 109, réalisée le 17/4/2007, |
