Descartes et les Mathématiques
Le cube en seconde
Ancienne version GéoSpace, adaptation à GeoGebra en cours.
La géométrie dans l'espace en seconde avec GeoGebra 3D: coin d'un cube - sections planes.
Sommaire
1. Longueur d'une diagonale d'un cube
3. Intersection d'une droite et d'un plan, avec un cube
4. Droite parallèle à un plan, dans un cube
5. Cube et droites parallèles
Droite parallèle à un plan, dans un cube
7. Les ambiguïtés de la perspective cavalière
8. Section plane d'un cube par un plan passant par trois des sommets
1. Comment calculer la longueur d'une diagonale d'un cube
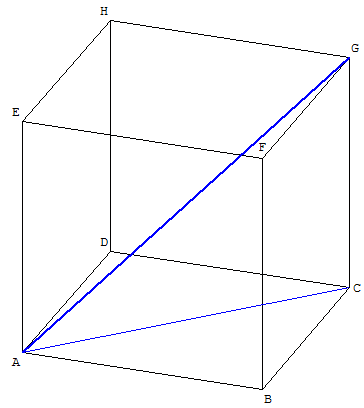
Dans le cube ABCDEFGH, de côté a, pour calculer la longueur de diagonale [AG], étudier le triangle rectangle ACG.
Dans le carré ABCD, AC2 = l2 a2, et la diagonale AC a pour longueur a
.
Avec le théorème de Pythagore dans ACG on a :
AG2 = AC2 + CG2 = 2 a2 + a2 = 3 a2.
La longueur d'une diagonale, du cube de côté a, est a
.
2.a. Coin d'un cube
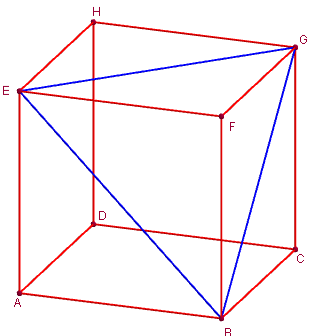
Coin de cube FBEG
Triangle médian dans un coin de cube
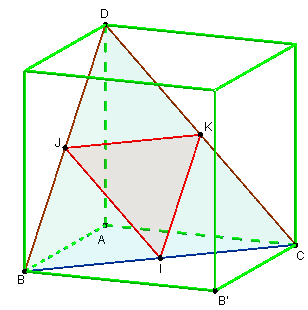
On appelle « coin de cube » le tétraèdre trirectangle ABCD formé par trois arêtes d'un cube concourantes en un sommet A, et des diagonales des faces du cube qui joignent les autres extrémités de ces arêtes.
Orthocentre d'un tétraédre trirectangle
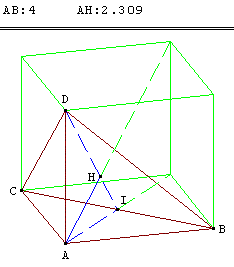
Soit H le projeté orthogonal de A sur le plan (BCD). Montrer que le point H est l'orthocentre du triangle BCD.
La droite (AD), perpendiculaire au plan (ABC), est orthogonale à toutes les droites de ce plan, en particulier à la droite (BC). Les arêtes opposées du coin de cube sont orthogonales. Le point A est l'orthocentre de ce tétraèdre trirectangle.
BCD est un triangle équilatéral. Si I, J et K sont les milieux des côtés de triangle, IJK est aussi un triangle équilatéral et, par exemple, la droite (JK), parallèle à (BC), est orthogonale à (AD).
2.b. Calcul de la hauteur AH
Dans la troisième figure ci-dessus, ABCD est un coin de cube de côté a = 4 cm et I le milieu de [BC]. (AH) est la hauteur abaissée sur la face (BCD).
Méthode 1 : calculer la longueur AH en exprimant de deux façons le volume V du tétraèdre ABCD, de base ABC et de sommet D.
L'aire de la base est égale à la moitié de celle du côté du cube, soit SABC = 
a2,, et la hauteur est AD = a.
Le volume est : V = 
× aire de la base × hauteur = SABC × a = 
a3.
V est aussi le volume du tétraèdre ABCD, de base BCD et de hauteur AH :
BCD est un triangle équilatéral de côté la diagonale du carré a. La hauteur de ce triangle équilatéral est DI = BD 
= a
.
SBCD = BC × DI = a × a = a2 .
V = SBCD × AH = × a2 × AH = a2 × AH.
On obtient la longueur AH = a
Méthode 2 : calcul d'inverses de carrés
Dans le triangle ABC rectangle en A de hauteur (AI) exprimer de deux façons l'aire :
2 Aire(ABC) = AI × BC = AB × AC et BC2 = AB2 + AC2
D'où AI2 = 
et 
De même, dans le triangle AID rectangle en A de hauteur (AH) : 
On trouve finalement 
Dans le cas particulier AB = AC = AD = a on retrouve la longueur AH = a
Application : En exprimant de deux façons différentes le volume du tétraèdre montrer que :
Aire2(BCD) = Aire2(ABC) + Aire2(ABD) + Aire2(ACD).
En classe de première, il est possible de généraliser avec un coin de pavé droit.
Voir aussi orthogonalité dans un cube : géométrie dans l'espace en TS et TES
3. Intersection d'une droite et d'un plan, avec un cube
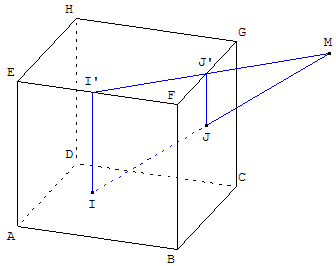
Dans le cube ABCDEFGH ci-contre, I et J sont deux points des faces (ABFE) et (BCGF).
Trouver le point d'intersection (éventuel) de la droite (IJ) avec la face (EFGH).
Indication
Trouver un plan (p) contenant la droite (IJ). Si ce plan n'est pas horizontal, il coupe le plan (EFG) selon une droite (d).
Lorsqu'il existe le point M, intersection des droites (d) et (IJ), est le point où la droite (IJ) rencontre le plan de la face supérieure du cube.
Par exemple, trouver un plan vertical contenant (IJ) :
Soit I’ la projection orthogonale de I sur la droite (EF) et J’ la projection de J sur (FG). (II’) et (JJ’) sont deux droites parallèles, les points I, J, I’ et J’ sont coplanaires dans un plan (p).
Les plans (p) et (IJ) se coupent selon la droite (I’J’).
Si les droites (IJ) et (I’J’) sont parallèles, la droite (IJ) est parallèle à la face (EFGH),
sinon elles se coupent en M qui est le point d'intersection de la droite (IJ) avec le plan (EFG).
Télécharger la figure GéoSpace cube_droite.g3w
4. Droite parallèle à un plan, dans un cube
Exemple de résolution d'un problème en utilisant diverses méthodes :
- Méthodes géométriques et règle d'incidence
- Méthode vectorielle
- Méthode analytique
Exercice
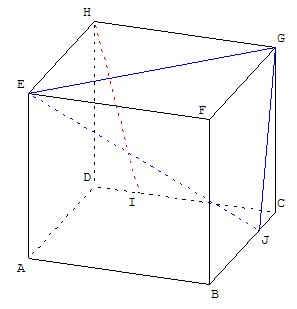
Sur les arêtes d'un cube de côté 4 cm, on place les points I et J tels que :
= 
et 
= 
.
Démontrer que la droite (HI) est parallèle au plan (EGJ).
Télécharger la figure GéoSpace cube_act.g3w
Cinq solutions
4.a. Méthode intuitive
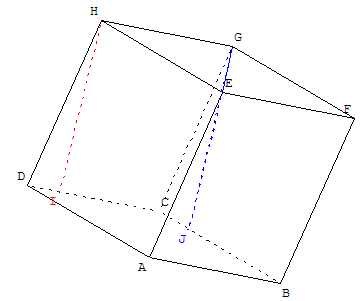
Pour s'en convaincre avec GeoGebra :
faire tourner la figure avec les touches CTRL + flèche droite jusqu'à ce que le plan (EGJ) soit vu parallèlement à l'axe de vision de l'observateur.
On constate que (HI) est bien parallèle à la trace de ce plan.
Télécharger la figure GéoSpace cube_ac2.g3w
4.b. Méthodes géométriques et règle d'incidence
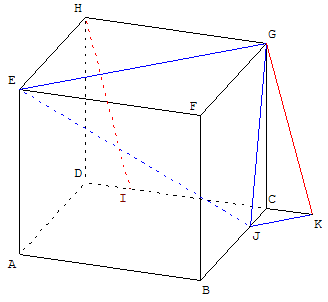
La parallèle à (HI) passant par G coupe (CD) en K. CK = CJ.
Le triangle rectangle isocèle CJK a deux côtés parallèles à ceux du triangle HEG, donc de même pour les troisièmes côtés on a (JK) // (EG), d'où (JK) est une droite du plan (EGJ). (HI) parallèle à la droite (GK) du plan (EGJ) est parallèle à ce plan.
Télécharger la figure GéoSpace cube_ac3.g3w
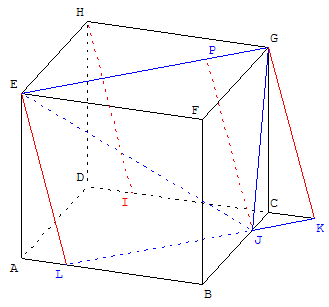
Avec le point L de [AB] tel que AL = AB/4, on peut faire une démonstration analogue plus difficile :
– en montrant que la droite (HI) est parallèle à la droite (EL)
– en utilisant le triangle rectangle isocèle BLJ égal aux trois quarts du triangle FEG,
– avec le parallélisme des bases, on vérifie que EGJL est un trapèze contenu dans le plan (EGJ).
Télécharger la figure GéoSpace cube_ac4.g3w
4.c. Méthode vectorielle
Utilisons comme dans la première méthode le point K tel que 
= = .
= 
+ = 
= 
+ .
Faire une introduction symbolique de pour trouver puis 
= −
:
= + ( - )
+ = + - +
= 
- ( + 
) = - = - 
est parallèle au plan comme combinaison linéaire de deux vecteurs de ce plan ; la droite (HI) est bien parallèle au plan (EGJ).
4.d. Méthode analytique
Dans le repère (G, , ) soit le point P de coordonnées (, 0).
Le vecteur 
a pour coordonnées (- , 1) ; il est donc égal au vecteur donc à .
On a donc = − + et on conclut comme ci-dessus.
5.a. Cube et droites parallèles
Dans le cube ABCDEFGH ci-contre, I est le milieu de [EF] et J le milieu de [FG].
La droite (BI) coupe (AE) en M et la droite (BJ) coupe (CG) en N.
Montrer que les droites (IJ) et (MN) sont parallèles.
Les points I et J sont placés sur les segments [EF] et [FG] de telle façon que EI = JG.
Montrer que les droites (IJ) et (MN) sont encore parallèles.
Figure 3D dans GeoGebraTube : cube et droites parallèles
Remarque : le triangle BIJ est la section plane du cube par le plan (BIJ).
5.b. Droite parallèle à un plan, dans un cube
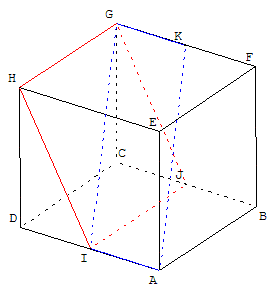
Dans le cube ABCDEFGH ci-contre I, J et K sont les milieux respectifs de [AD], [BC] et [FG].
Montrer que le quadrilatère AIGK est un parallélogramme.
Montrer que la droite (AK) est parallèle au plan (HIJ) :
Démontrer que le vecteur 
est combinaison linéaire de 
et 
,
puis avec le parallélogramme, montrer que la droite (AK) est parallèle à (IG), qui est incluse dans le plan (HIJ).
Télécharger la figure GéoSpace cube_parallelogramme.g3w
Voir : activités
6. Section de cube et patrons
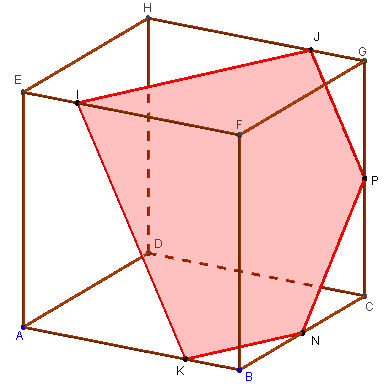
Coupe d'un cube par un plan
Un point I est placé sur l'arête [AB] d'un cube ABCDEFGH. Par exemple tel que AI = 
AB.
Sur les arêtes parallèles [DC] et [EF], on place les points J et K tels DJ = EK = AI.
Il s'agit de construire, en papier Canson, les deux morceaux du cube découpé par le plan (IJK).
Figure 3D dans GeoGebraTube : pentagone comme section du cube
6.a. Tracé de la section plane en perspective
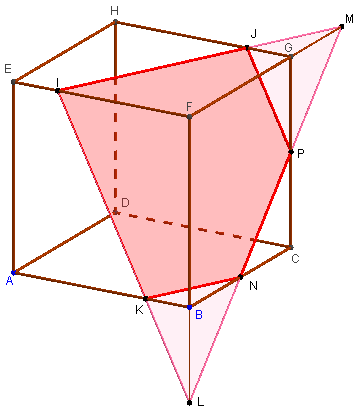
Comment construire une section d'un cube par un plan
Calcul de la position du point M. (Mise en équation utilisant le théorème de Thalès : MD = AD), puis des points L, P et N.
6.b. Dessin en vraie grandeur de la section plane
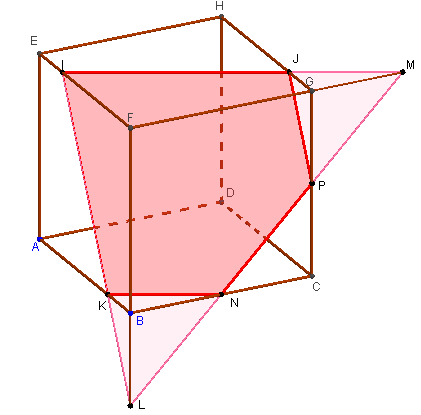
Technique : obtenir une vue de face du plan (IJK).
Vérifier que N et P partagent [ML] en trois segments de longueur égale.
Tracer le pentagone IJPNK. Vérifier que deux paires de côtés sont parallèles et que (NP) est parallèle à la diagonale (KJ).
6.c. Les deux parties du cube (GéoSpace)
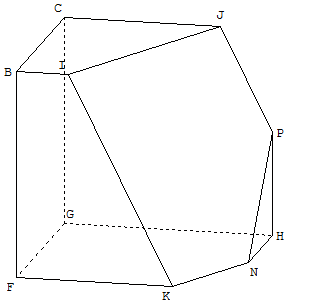
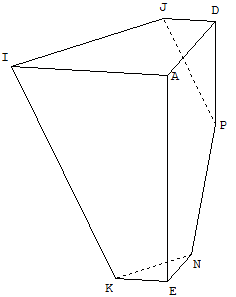
Télécharger les figures GéoSpace sec_cube_part1.g3w ; sec_cube_part2.g3w
7. Les ambiguïtés de la perspective cavalière
Faire un losange à partir d'un cube.
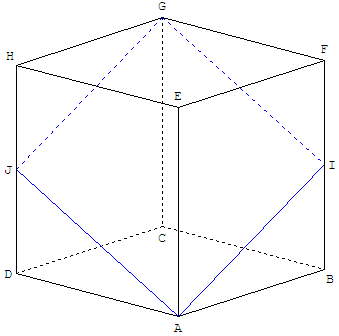
ABCDEFGH est un cube. I est le milieu de [BF]
et J est le milieu de [DH].
Les côtés du quadrilatère AIGJ sont de même longueur.
C'est un losange.
Le dessin suggère que les angles sont droits ?
Télécharger la figure GéoSpace sec_cube4.g3w
Une vue de face du plan
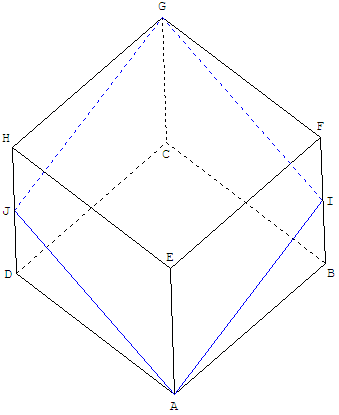
Une vue de face du plan (IAJ) montre que le losange AIGJ n'est pas un carré
Les fervents du calcul peuvent démontrer que les diagonales du losange sont inégales : IJ = AC < AG.
8. Section par un plan passant par trois des sommets du cube
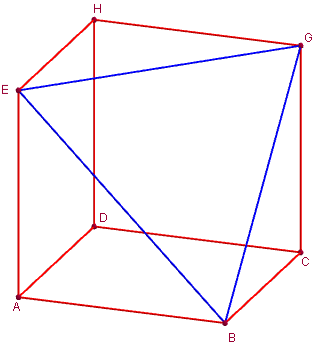
Cube fortement tronqué
Section plane du cube
Dans le cube ABCDEFGH, la section plane déterminée par les trois sommets des côtés d'extrémité F, autres que F, est un triangle équilatéral BEG, formé par trois diagonales de faces du cube.
« Cube » moins « coin de cube »
Le polyèdre formé par le cube, auquel on enlève le coin de cube BEGF, est le « cube fortement tronqué » ABCDEGH.
Figures 3D dans GeoGebraTube : coin de cube dans un cube en fil de fer
– On y trouve les trois variantes : triangle équilatéral formé par trois diagonales de faces concourantes du cube
– cube moins coin de cube
– cube fortement tronqué
Sol LeWitt
Arts conceptuels
Figure 3D dans GeoGebraTube : cube fortement tronqué - Sol LeWitt
Tétraèdre inscrit dans un cube
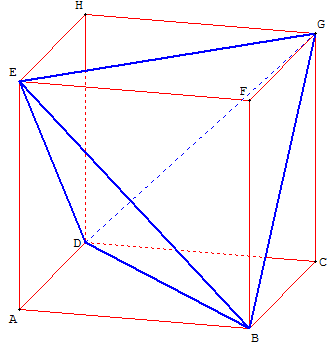
Tétraèdre régulier BDEG inscrit dans le cube ABCDEFGH.
Les côtés du tétraèdre sont des diagonales de faces du cube.
Le tétraèdre régulier a un volume égal au tiers de celui du cube. Il est bordé de quatre coins de cube qui ont donc un volume égal au sixième de celui du cube.
Figure 3D dans GeoGebraTube : tétraèdre inscrit dans un cube
Table des matières
…Avec GeoGebra 3D dans d'autres pages du site
Sections planes d'un cube
Sections de cube en 3e
Sections de cube dans l'ancienne 1S
Plan perpendiculaire à une diagonale : produit scalaire en 1ère S
Figures 3D dans GeoGebraTube : cube,
L'espace en seconde
Lien
Mobile friendly
Page no 138, créée le 17/3/2009
adaptée à GeoGebra 3D le 4/2/2015