Descartes et les Mathématiques
Produit scalaire dans l'espace
Droites orthogonales : tétraèdre et cube - Figures avec GeoGebra.
Sommaire
Définitions
1. Tétraèdre : arêtes égales
2. Tétraèdre : arêtes orthogonales
3. Plan et droite orthogonaux dans le cube
GéoPlan : Produit scalaire
Liens vers les pages tétraèdre
Tétraèdre orthocentrique : tétraèdre en 2nde
Sections planes d'un tétraèdre
Liens vers les pages section de cube
Plan et droite orthogonaux dans le cube - épreuve pratique de TS
Définitions
Deux vecteurs de l'espace pouvant toujours être placés dans un même plan, les trois premières définitions du produit scalaire dans l'espace sont équivalentes à celles données en 1ère S pour le produit scalaire dans le plan.
Définition 1 (projection orthogonale)
Le produit scalaire de deux vecteurs 
et 
colinéaires est égal à AB × CD s'ils sont de même sens, et à – AB × CD s'ils sont de sens contraires.
Pour calculer le produit scalaire . de deux vecteurs non colinéaires, dans le plan déterminé par et , on peut remplacer le vecteur par sa projection orthogonale sur le vecteur .
Définition 2 (carré des normes)
si 
= , |||| = |||| = AB.
On appelle produit scalaire de deux vecteurs le nombre : .
= 
[ || + ||2 - ||||2 - ||||2 ].
Définition 3 (expression trigonométrique)
. = |||| × |||| × cos θ, où θ est l'angle (, ) formé par les directions des vecteurs.
Définition 4 (expression analytique dans l'espace)
Si dans un repère orthonormal (O, 
, 
, 
), et ont pour coordonnées respectives (x, y, z) et (x’, y’, z’), alors . = xx’ + yy’ + zz’.
Définition simple et calculs faciles. On retrouve xx’ + yy’ + zz’= 0 pour les vecteurs orthogonaux.
On retrouve aussi le calcul de distance de deux points : |||| = 
= AB, où x et y sont les coordonnées de .
Il faut admettre que le calcul du produit scalaire est indépendant du choix du repère.
Équation cartésienne d'un plan
Le plan passant par un point A et de vecteur normal 
est l'ensemble des points M tels que 
. = 0.
Dans un repère orthonormal un plan (p) a une équation de la forme ax + by + cz = d où les réels a, b, c ne sont pas simultanément tous nuls.
(a, b, c) est un vecteur normal à (p).
En effet, si M a pour coordonnées (x, y, z), A(x0, y0, z0) et (a, b, c), alors (x-x0, y-y0, z-z0) et . = a(x-x0) + b(y-y0) + c(z-z0).
Le produit scalaire est nul si ax + by + cz = ax0 + by0 + cz0. Le nombre d s'obtient en calculant ax + by + cz pour les coordonnées de A.
1. Tétraèdre : arêtes de longueurs égales
Produit scalaire dans un tétraèdre ayant deux arêtes de longueurs égales
Soit ABCD un tétraèdre et I, J, K et L les milieux de [BC], [BD], [CA] et [DA].
Étude des bimédianes [LI] et [KJ].
1. Exprimer 
et 
en fonction de et .
Remarque : décomposer en une somme de deux vecteurs et utiliser le théorème des milieux.
De même avec .
2. Calculer le produit scalaire . .
3. Montrer que les bimédianes (LI) et (KJ) sont orthogonales si et seulement si :
AB = CD.
Remarque : IJLK est un carré, de centre G, centre de gravité du tétraèdre.
Figures 3D dans GeoGebraTube : bimédianes perpendiculaires d'un tétraèdre
2. Tétraèdre : arêtes orthogonales
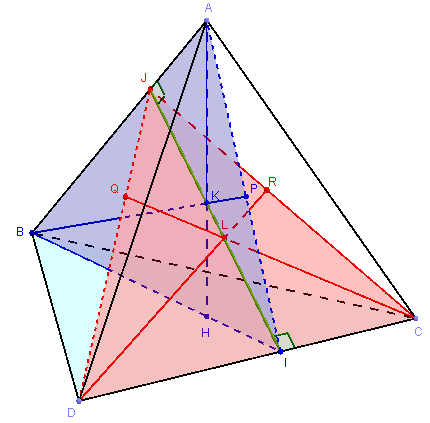
Rappel : forme vectorielle du « théorème de la médiane »
Soit C et D deux points de l'espace et I le milieu de [CD].
Quel que soit le point M de l'espace, la médiane MI du triangle MCD permet d'écrire :
+ 
= 2 
et MC2 - MD2 = 2 .
.
En effet : +
= ( + 
)
+ ( + 
)
= 2
et MC2 - MD2 = ( + ).(- ) = 2 .(
+ ) = 2 ..
Exercice
Bac S - Besançon 1989
On considère quatre points distincts A, B, C et D de l'espace.
1. Exprimer AC2 - AD2 et BC2 - BD2 sous la forme de produits scalaires.
2. Démontrer que les droites (AB) et (CD) sont orthogonales si et seulement si :
AC2 + BD2 = AD2 + BC2.
3. Application : on suppose que le tétraèdre ABCD soit tel que les arêtes (AB) et (CD) soient orthogonales ainsi que les arêtes (BC) et (AD). Montrer alors qu'il en est de même des arêtes (BD) et (AC).
(On dit alors que ABCD est un tétraèdre orthocentrique.)
Figures 3D dans GeoGebraTube : tétraèdre orthocentrique
3. Plan et droite orthogonaux dans le cube
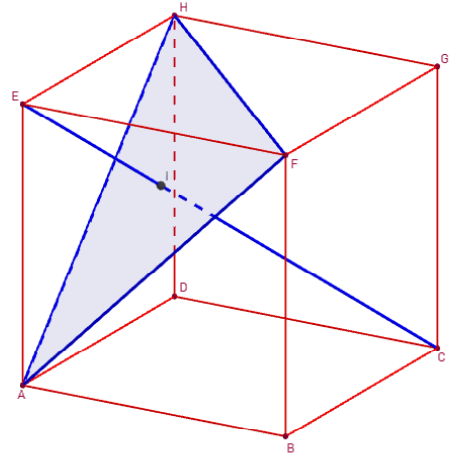
On considère un cube ABCDEFGH, d'arête de longueur a (a réel strictement positif). Soit I le point d'intersection de la droite (EC) et du plan (AFH).
Problème d'incidence
Montrer que la droite (EC) est perpendiculaire au plan (AFH).
Figure 3D dans GeoGebraTube : triangle équilatéral formé par trois diagonales de faces concourantes du cube
Produit scalaire
ÉduSCOL - Terminale S – Banque de sujets 2007 - Sujet 023 (enseignement obligatoire)
• Calculer, en fonction de a, les produits scalaires suivants :
.
, ., 
.
• En déduire que les vecteurs 
et sont orthogonaux,
le point I est alors le projeté orthogonal de E sur le plan (AFH),
les droites (EI) et (AF) sont orthogonales.
• Justifier le résultat suivant : les droites (EH) et (AF) sont orthogonales.
En déduire que la droite (HI) est orthogonale à la droite (AF).
• Établir, de même, que la droite (FI) est orthogonale à la droite (AH).
• Que représente le point I pour le triangle AFH ?
Solutions - Problème d'incidence
La droite (HF) est orthogonale à (EC) :
Les deux diagonales (HF) et (EG) du carré EFGH sont perpendiculaires.
La droite (EA) perpendiculaire au plan EFH est perpendiculaire à la droite (HF) contenue dans ce plan.
La droite (HF) perpendiculaire aux droites (EG) et (EA) du plan AEG est perpendiculaire à ce plan.
(HF) est orthogonale à toute droite du plan AEG, en particulier à la droite (EC).
On démontre, de même, que la droite (AF) est orthogonale à (EC) : en effet, (AF) est perpendiculaire à (BE) et à (BC).
(AF) est donc perpendiculaire au plan EBC, et à la droite (EC) contenue dans ce plan.
La droite (EC) orthogonale aux deux droites concourantes (HF) et (AF) du plan AFH est orthogonale à ce plan.
Produit scalaire
. = .(
+
) = − 2 + . = − a2+ 0 = − a2, car et sont orthogonaux,
. = .(+) = 0 + 2 = a2,
est orthogonal au plan AEF, donc à : . = 0.
. = (++). = − a2 + a2 + 0 = 0, et sont orthogonaux.
La droite (EI) est perpendiculaire à la droite (AF).
La droite (EH) perpendiculaire au plan AEF est orthogonale à la droite (AF) contenue dans ce plan.
La droite (AF) perpendiculaire aux droites concourantes (EI) et (EH) est perpendiculaire au plan EHI contenant ces deux droites.
(AF) est perpendiculaire à la droite (HI) contenue dans ce plan.
Le point I intersection des hauteurs (HI) et (FI) du triangle AFH est l'orthocentre du triangle.
Les côtés du triangle AFH sont égaux comme diagonales des faces du cube de longueur a
, AFH est un triangle équilatéral, le point I est le centre du triangle.
Table des matières
GéoPlan Produit scalaire
Mobile friendly
…Avec GeoGebra 3D dans d'autres pages du site
Mode d'emploi GeoGebra 3D
GéoSpace : Activités au lycée
TS - TES : Géométrie de l'espace
Copyright 2015 - © Patrice Debart
Page no 76, réalisée le 22/9/2004
adaptée à GeoGebra le 10/2/2015