Descartes et les Mathématiques
Sections planes d'un cube
La géométrie dans l'espace dans l'ancienne 1ère S
Triangle, quadrilatère, pentagone et hexagone comme sections avec GeoGebra 3D.
Intersection d'un plan avec les faces du cube
2. Constructions de sections par des plans variables
3. Variation de la section par un plan variable
4. Un sommet et deux points sur les arêtes
5.a. Trois points sur des arêtes concourantes
5.b. Trois points sur des arêtes non concourantes
6. Trois points sur des arêtes disjointes
Section d'un cube par un déterminée par trois points
Sections planes : avec GeoGebra 3D, on crée la section plane avec l'outil intersection de surfaces.
Avec la souris, il n'est pas facile de sélectionner tout le cube et souvent on ne sélectionne qu'une seule face.
On a intérêt à montrer le plan, puis dans le menu algèbre, sélectionner le cube a ;
ou bien, en bas de l'écran, saisir d=IntersectionChemins[Plan[A,B,C], a]
Dès que l'on tape d=Int le logiciel propose la syntaxe précise :
d=IntersectionChemins[<Plan>, <Polygone>]
Remplacer les <...> par le nom du plan et celui du cube.
Géométrie pratique
- Une solution non conformiste, piochée de-ci, de-là dans l'exercice 497-3 de l'APM, consiste à marquer les trois points sur un cube et de le plonger délicatement dans un bain de teinture colorée.
En retirant le cube, la section apparaît. - Une autre solution consiste à remplir d'eau un bidon en plexiglas transparent que l'on a percé à l'emplacement des trois points.
En inclinant le bidon, de telle façon que l'eau sorte par les trois trous, le niveau d'eau donne la section. - Une dernière solution consiste à traverser ce cube, en plexiglas transparent, par un balayage de rayons laser passant par les trois points.
En général, dans les exercices ci-dessous nous décrivons la construction point par point des sections, en explicitant les divers cas particuliers.
1. Sections déterminées par trois points sur les arêtes
« L'utilisation de l'informatique permet une vision dynamique de la figure. GeoGebra permet de faire tourner le cube et de mettre en évidence la section cherchée. La possibilité de placer un plan isolé de face permet de voir les sections planes en “vraie grandeur”
1.a. Cube
ABCDEFGH est un cube.
Figures 3D dans GeoGebraTube : cube, cube en fil de fer
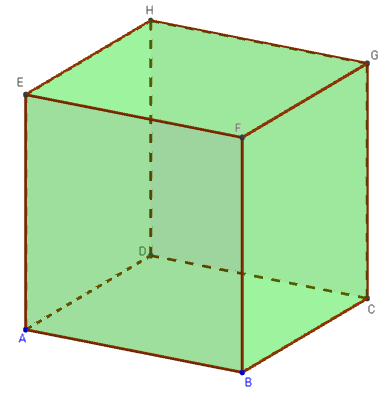
1.b. Plan déterminé par trois points sur trois arêtes concourantes
Créer les points variables I, J et K sur les arêtes respectives [FB], [FE] et [FG], concourantes au même sommet F.
Déplacer les points I, J et K et observer la section obtenue.
Figure 3D dans GeoGebraTube : triangle comme section plane du cube
Voir l'intersection du plan (MNP) avec les six faces du cube
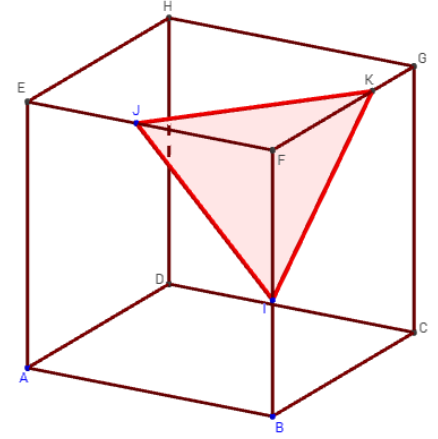
1.c. Deux points sur deux arêtes concourantes et un troisième
Modifier le point K pour qu'il se déplace maintenant sur l'arête [DC],
créer la section du cube par le plan (IJK),
déplacer les points I, J et K et observer les diverses sections obtenues :
si ces points ne sont pas des sommets du cube, on trouve des pentagones ou hexagones ayant deux ou trois paires de côtés parallèles..
Figure 3D dans GeoGebraTube : sections d'un cube déterminées par trois points
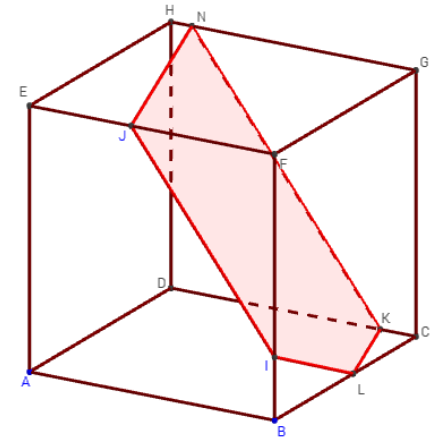
1.d. Points sur des arêtes disjointes dans les trois directions
Modifier maintenant le point K pour qu'il se déplace sur l'arête [EH],
créer la section du cube par le plan (IJK),
déplacer les points I, J et K et observer les diverses sections obtenues:
Si ces points ne sont pas des sommets du cube, on trouve des hexagones ayant des côtés deux à deux parallèles.
Lorsque I, J et K sont les milieux des côtés, on a l'hexagone régulier de Bergson.
Figure 3D dans GeoGebraTube : hexagone comme section d'un cube
2. Constructions de diverses sections par des plans parallèles
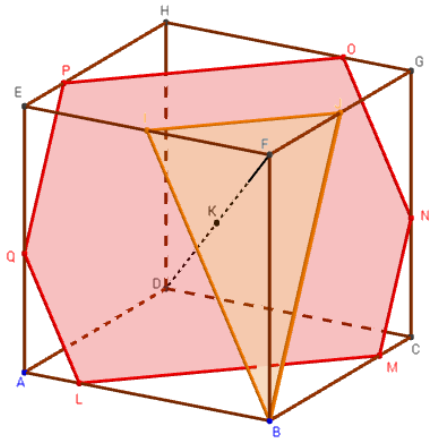
2.a.Triangle BIJ et section par un plan parallèle
I est le milieu de [EF], J est le milieu de [FG].
Le triangle BIJ est la section du cube avec le plan (BIJ).
On mène par un point K, situé sur [DF], le plan (P) parallèle au plan (BIJ).
Construire la section du cube avec le plan (P).
Figures 3D dans GeoGebraTube : section d'un cube par un plan variable
2.b.Triangle équilatéral et section par un plan parallèle
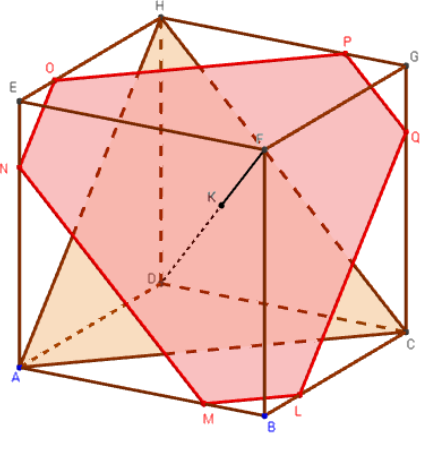
Triangle équilatéral ACH, formé par trois diagonales, et section par un plan parallèle passant par un point K
Construire le triangle ACH, section du cube avec le plan (ACH).
Soit K un point de la diagonale [DF].
Trouver l'intersection du cube avec le plan parallèle au plan (ACH) passant par K.
Figures 3D dans GeoGebraTube : section d'un cube parallèle à trois diagonales
3. Section variable par un plan perpendiculaire à une diagonale
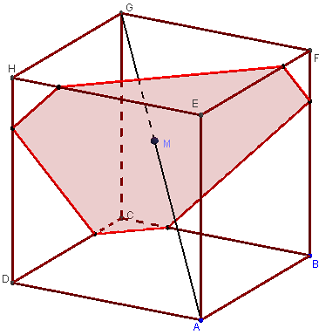
Trouver l'intersection d'un cube ABCDEFGH avec le plan parallèle à (BDE) passant par un point M variable sur la diagonale (AG) du cube.
Hexagone de Bergson
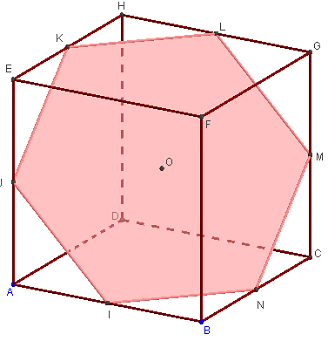
Si M est en O, centre du cube, on a l'hexagone régulier du problème de Bergson.
Figure avec le plan médiateur de [DF].
Section variable d'un cube
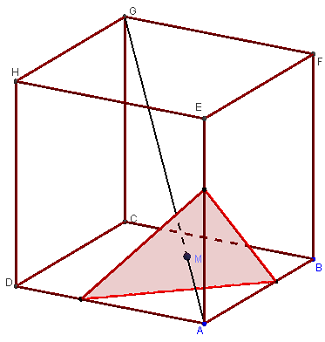
Lorsque le point M se déplace, il défile une succession de triangles, hexagones puis triangles.
En orientant différemment le plan sécant, on peut obtenir le défilement d'une succession de polygones : triangle, quadrilatère, pentagone, hexagone, pentagone, quadrilatère, triangle.
Les métamorphoses d'un type au type suivant ayant lieu lorsqu'un sommet du cube traverse le plan variable.
Figures 3D dans GeoGebraTube : section variable d'un cube
hexagone de Bergson comme section plane du cube
Voir : GeoGebra en 3e : sections planes d'un cube
Étude du plan BDE : produit scalaire
4.a. Parallélogramme comme section d'un cube
ABCDEFGH est un cube de côté 4 cm. I est le milieu de la face BCGF et J celui de EFGH.
a. Calculer la longueur AI.
b. Trouver les traces du plan (AIJ) sur le cube.
Indications
Calcul de AI2
Soit T le milieu de [BC] et a le côté du carré.
Dans triangle rectangle horizontal ABT, avec Pythagore on a :
AT2 = AB2 + BT2 = a2 + a2/4.
Dans triangle rectangle vertical ATI, on a :
AI2 = AT2 + TI2 = (a2 + a2/4) + a2/4 = a2 + a2/2 = 
a2.
Section plane
Trouver le point K intersection de la droite (IJ) et du plan (ABC).
U étant le centre du carré ABCD, en étudiant le plan (UIJ) on remarque que K est le symétrique de U par rapport à (BC).
La droite (AK) coupe (BC) en P sommet de la section plane.
L'intersection de (PI) et de (FG) est le point Q.
De même, la droite (QJ) coupe (EH) en R.
Le parallélogramme APQR est la section plane du plan (AIJ) sur le cube.
Figure 3D dans GeoGebraTube : parallélogramme comme section d'un cube
4.b. Trapèzes comme section du cube
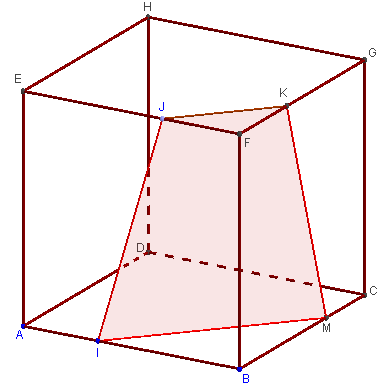
– I est un point de l'arête [AB] du cube ABCDEFGH.
J et K sont deux points des arêtes concourantes [EF] et [FG].
– Construire la section plane du cube par le plan (IJK).
Indications
Comme les faces (ABCD) et (EFGH) du cube sont parallèles, le plan (IJK) coupe le plan (ABC) suivant une parallèle (d) à (JK).
Trapèze lorsque la section coupe l'arête [BC]
La droite (d) coupe (BC) en M.
Lorsque M est à l'intérieur du segment [BC], [IM] est la trace du plan (IJK) sur la face (ABCD).
[IJ] et [MK] sont alors les deux autres côtés de la section IMKJ, qui est un trapèze de bases [IM] et [JK].
Figure 3D dans GeoGebraTube : deux trapèzes comme section plane du cube
Autre trapèze lorsque la section coupe l'arête [CD]
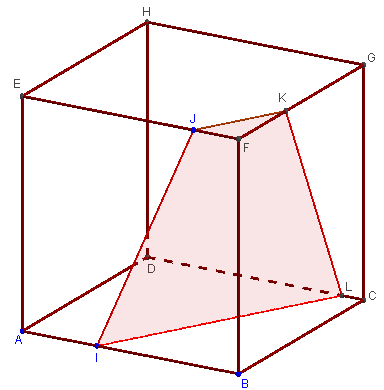
La droite (d) coupe (CD) en L.
Lorsque L est à l'intérieur du segment [CD], [IL] est la trace du plan (IJK) sur la face (ABCD).
[IJ] et [LK] sont alors les deux autres côtés de la section ILKJ, qui est un trapèze de bases [IL] et [JK].
Voir aussi : autre trapèze comme section par un plan contenant un sommet
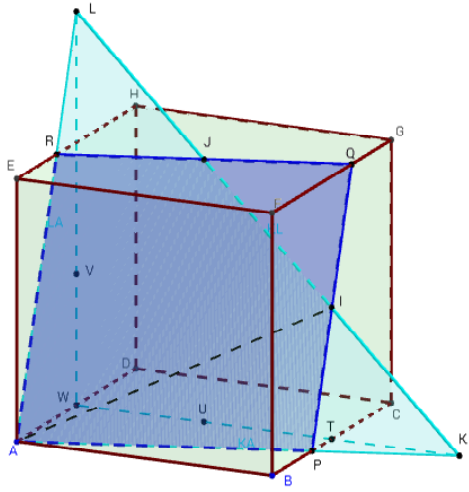
5.a. Intersection, avec les prolongements des faces du cube
Plan déterminé par trois points sur des arêtes concourantes
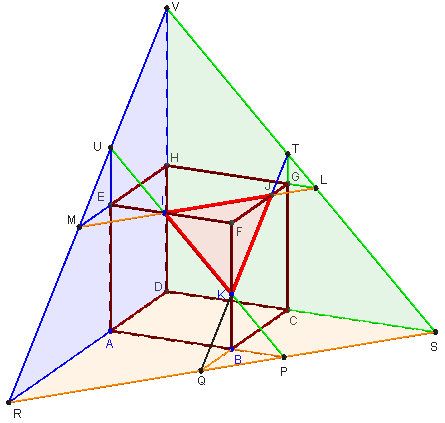
I, J et K sont trois points des arêtes [FE], [FG] et [FB] (concourantes en F) du cube ABCDEFGH.
Trouver l'intersection du plan (IJK) avec les six faces du cube.
Sur chacune des droites d'intersection, on trouvera les quatre points d'intersection avec les prolongements des côtés du carré.
Tracez les segments [IJ], [JK] et [IK] sur les faces du cube.
La section plane est le triangle IJK.
– Trouver la droite (PQ), intersection de (IJK) avec le plan (ABC).
Tracez le point P intersection de (IK) et (AB) et le point Q intersection de (JK) et (BC), puis la droite (PQ), intersection de (IJK) avec le plan (ABC). La droite (PQ) coupe (DA) en R et (DC) en S.
Les points R, Q, P et S sont donc alignés.
Les droites (PQ) et (IJ) sont parallèles.
– Trouver la droite (LS), intersection de (IJK) avec le plan (CDH).
Prolongez (IJ) jusqu'à son intersection L avec la droite (HG).
Ce point L est situé dans le plan (CDH). La droite (LS) est l'intersection de (IJK) avec le plan (CDH).
Cette droite (LS) est parallèle à (IK). Elle coupe (DH) en V et (CG) en T.
Les points V, T, L et S sont donc alignés.
– Trouver la droite (VR), intersection de (IJK) avec le plan (ADE).
Cette droite coupe le côté (HE) en M situé sur (IJ) et coupe le côté (AE) en U situé sur (IK).
Les points V, U, M et R sont donc alignés.
Les droites (VR) et (JK) sont parallèles.
Figure 3D dans GeoGebraTube : prolongement d'une section triangulaire du cube
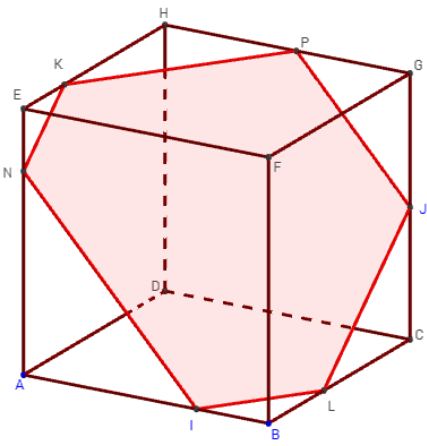
5.b. Intersection, avec la base d'un cube
Plan déterminé par trois points I, J et K sur les arêtes
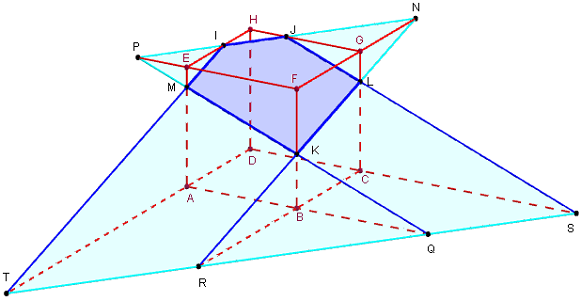
Comment construire un pentagone comme section d'un cube par un plan
(Les trois arêtes ne sont pas concourantes.)
– I et J sont deux points des arêtes concourantes [HE] et [HG] du cube ABCDEFGH.
K est sur l' arête [BF].
– Tracer la section plane déterminée par le plan (IJK).
– Trouver l'intersection de (IJK) avec le plan de base (ABC).
Indications
– Tracer le point N, intersection de (IJ) avec le côté (FG), puis le point P intersection de (IJ) avec le côté (EF).
La droite (KN) coupe le côté [CG] en L et la droite (KP) coupe le côté [AE] en M.
Le pentagone IJLKM est la section du cube par le plan (IJK).
– Construire le point Q intersection de (KP) avec (AB), puis le point R intersection de (KN) avec (BC).
L'intersection de (IJK) avec le plan (ABC) est la droite (QR).
Cette droite est parallèle à (IJ).
Les points d'intersection T et S sont aussi sur cette droite (QR).
Figure 3D dans GeoGebraTube : pentagone comme section du cube
5.c. Cas particulier : I et J milieux des côtés
– I et J sont les milieux des arêtes concourantes [AB] et [BC] du cube ABCDEFGH.
K est un point sur l' arête [DH].
– Tracer la section plane de (IJK) avec le cube.
– Trouver l'intersection de (IJK) avec le plan (EFG),
étudier l'intersection des plans (IJK) et (ACH).
Indications
– Tracer le point P, intersection de (IJ) avec le côté (AD), puis le point N intersection de (IJ) avec le côté (CD).
La droite (KP) coupe le côté [BF] en M et la droite (KN) coupe le côté [CG] en L.
Le pentagone IJLKM est la section du cube par le plan (IJK).
– La droite (IJ) est parallèle à la diagonale (AC), puisque (IJ) est une droite des milieux du triangle ABC.
La droite (IJ) est incluse dans le plan (IJK) et la droite (AC) est incluse dans le plan (ACH).
Les points T, intersection de [KM] et [AH] et S intersection de [KL] et [CH] sont à l'intersection de ces plans (IJK) et (ACH).
D'après le théorème du toit, la droite (TS), intersection des deux plans, est parallèle aux droites (IJ) et (AC).
Elle est donc parallèle à la face (ABCD).
Figure 3D dans GeoGebraTube : section d'un cube et milieux de deux arêtes
6. Intersection, avec le prolongement de la face de base du cube
Plan déterminé par trois points I, J et K sur 3 arêtes
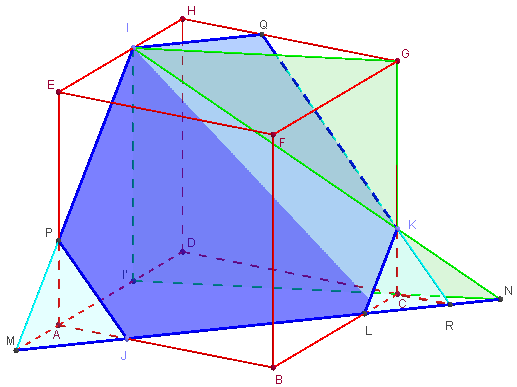
(Aucune des trois arêtes ne sont concourantes.)
« Section d'un cube par un plan formé de 3 points sans face commune »
Intersection, avec une face de base d'un cube, du plan déterminé par trois points I, J et K sur des arêtes.
– I, J et K sont trois points des arêtes [EH], [AB] et [CG], non concourantes, du cube ABCDEFGH.
– Trouver la section du plan (IJK) sur le cube.
Exercice assez difficile : il faut utiliser un plan auxiliaire (ICG) pour trouver le point N, aligné avec I et K, situé dans le plan de base (ABC) du cube ; puis terminer la construction, comme pour l'exercice précédent,.avec la droite (NM) d'intersection du plan (IJK) de la section avec la face (ABC) du cube.
Indications
– Trouver l'intersection N de la droite (IK) avec le plan horizontal (ABC). GeoGebra 3D trouve facilement ce point.
Pour une construction géométrique dans le plan auxiliaire vertical (ICG), tracer la parallèle (II’) à (GC) passant par I. Le point N est à l'intersection de (I’C) avec (IK).
– Trouver ensuite le point d'intersection L de la droite (NJ) avec l'arête (CB) du cube, puis les points M sur (AD) et R sur (CD), situés sur les prolongements des faces latérales, puis terminer en trouvant le point P intersection de (MI) et de (AE), enfin le point Q sur (RK) et (HG).
La section plane IPJLKQ est un hexagone ayant ses côtés opposés parallèles deux à deux.
Figure 3D dans GeoGebraTube : section hexagonale du cube
Cas particulier : I, J et K milieux des côtés, voir l'hexagone régulier du problème de Bergson
7. Intersection avec les prolongements des faces d'un cube
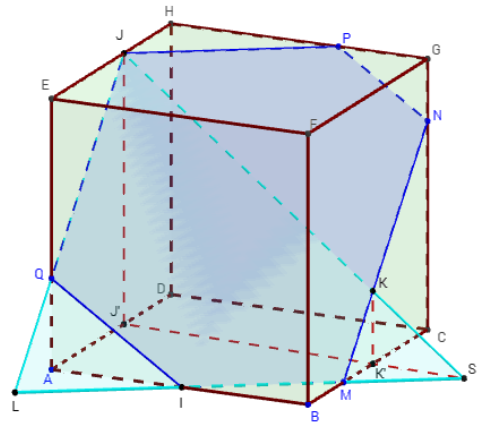
Section du plan déterminée par deux points I, J sur 2 arêtes et un point K sur une des faces
– I et J sont deux points des arêtes [AB] et [EH] du cube ABCDEFGH.
K est à l'intérieur de la face (BCGF).
– Trouver les intersections du plan (IJK) avec les faces du cube.
Indications
– Trouvez la droite d'intersection du plan vertical contenant J et K avec la face ABCD.
Pour cela, tracer les projections J’ et K’ des points J et K sur le plan horizontal.
Les droites (JK) et (J’K’) se coupent en S.
– Tracer les points d'intersection de (SI) avec les côtés (BC) et (AD), et terminer la section plane avec le point P, sachant que (JP) est parallèle à (SI).
Figure 3D dans GeoGebraTube : pentagone comme section d'un cube
8. Section déterminée par trois points situés sur les faces
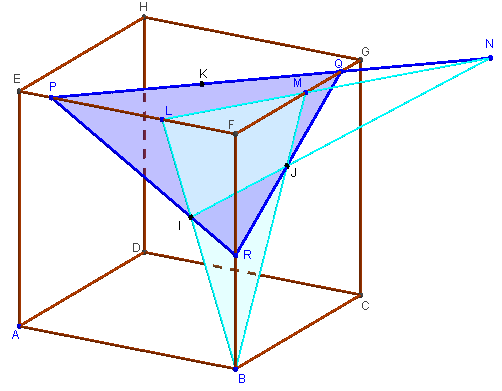
Faces ayant un sommet commun F
(Figure restreinte au cas où les points P, Q et R restent sur ces arêtes issues de F.)
– I, J et K sont trois points à l'intérieur de 3 faces (ABFE), (BCGF) et (EFGH) du cube ABCDEFGH.
– Trouver les intersections du plan (IJK) avec les faces (BEF), (BFG) et (EFG) du cube.
Indications
– Tracer le triangle BLM, section plane du cube avec le plan (BIJ). Trouvez la droite d'intersection (LN) du plan (BIJ) avec la face EFGH.
Les deux droites (LN) et (IJ) se coupant en N, point situé dans les plans (IJK) et (EFG).
Montrez que la droite (KN) est l'intersection de ces deux plans. Déduisez-en que sur la droite d'intersection (KN), le point P de l'arête [EF] et le point Q de l'arête [FG] sont deux points du plan (IJK).
– Tracez le troisième point R sur l'arête [BE], en prolongeant les droites (PI) et (QJ).
Les droites (PR) et (RQ) sont les intersections de (BEF) et (EFG) avec le plan (IJK).
Figure 3D dans GeoGebraTube : section plane du cube déterminée par trois points des faces
Table des matières
Les figures de cette page avec GéoSpace
…Avec GeoGebra 3D dans d'autres pages du site
Sections planes du cube
GeoGebra 2nde : incidence et cube en seconde
Cube en troisième Section d'un cube par un plan parallèle à une arête.
Plan et droite orthogonaux dans le cube, à l'épreuve pratique de TS
Problème de Bergson à l'épreuve pratique de TS
GeoGebra 2deTétraèdre
Sections planes d'un tétraèdre
Bac S 2014 : optimisation dans un tétraèdre trirectangle
Google friendly
Copyright 2002 - © Patrice Debart
Page no 18, réalisée le 14/3/2002
adaptée à GeoGebra 3D le 13/2/2015