Descartes et les Mathématiques
La géométrie en troisième
avec GeoGebra 3D
Problèmes de sections planes de solides
Sphère, représentation en perspective.
GeoGebra en 3e
2. Sections et tronc de pyramide
3. Section et tronc de tétraèdre - Solide composite - Lanterne
Travaux Pratiques 1
A. Sections planes d'un cube
« L'utilisation de l'informatique donne une vision
dynamique de la figure. GeoGebra permet de
faire tourner le cube et de mettre en évidence la
section cherchée. La possibilité de placer un plan
isolé en “vue de face” permet de voirles
sections planes en “ vraie grandeur ”.
Sections planes : En général, dans les exercices
ci-dessous, nous décrivons la construction point
par point des sections, en explicitant les divers
cas particuliers.
Technique GeoGebra 3D
Avec GeoGebra 3D, on crée la section plane
avec l'outil intersection de surfaces.
Avec la souris, il n'est pas facile de
sélectionner tout le polyèdre
et souvent
on ne sélectionne qu'une seule face.
On a intérêt à montrer le plan, puis dans le
menu algèbre, sélectionner le solide a ;
ou bien, en bas de l'écran, saisir
d=IntersectionChemins[Plan[A,B,C], a]
Dès que l'on tape d=Int le logiciel propose la syntaxe précise :
d=IntersectionChemins[<Plan>, <Polygone>]
Remplacer les <...> par le nom du plan et celui du polyèdre.
Section du cube par un plan contenant une arête
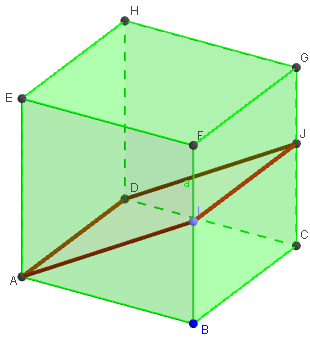
Créer le point variable I, sur le segment (arête du cube) [BF].
Trouver le point J intersection du plan (ADI) avec la droite (CG).
Tracer les segments [AI], [IJ] et [JD].
Déplacer le point I.
Quelle est la nature de la section du cube par le plan (ADI) ?
Face (ABFE) de profil
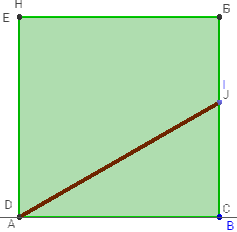
Faire tourner la figure pour visualiser le profil
de la section plane du cube en vraie grandeur.
Figure 3D dans GeoGebraTube :
rectangle comme section d'un cube
1.2. Carré - rectangle
Section d'un cube par un plan parallèle à une arête.
La section par un plan parallèle à une arête est un
rectangle,
dans le cas où le plan est parallèle à une
face, la section est un carré.
1.3. Trapèze comme section plane du cube
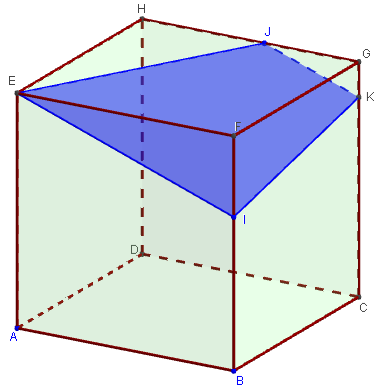
Section plane déterminée par un sommet
et deux points sur les arêtes du cube
I et J sont deux points sur les arrêtes [BF] et [GH],
arrêtes orthogonales non concourantes,
ne contenant pas le sommet E.
Trouver l'intersection du plan (EIJ) avec les faces du cube.
Indications
– Mener par J, la parallèle (d) à (EI) :
Comme les faces (ABFE) et (CDHG) du cube
sont parallèles, le plan (EIJ) coupe le plan
(CDH) suivant cette parallèle (d) à (EI).
La droite (d), située dans la face (CDHG), coupe (CG) en K.
– La section plane EIKJ est un trapèze.
[EJ] et [IK] sont les deux autres côtés
du trapèze EIKJ de bases [EI] et [JK].
Figure 3D dans GeoGebraTube :
trapèze comme section plane d'un cube
Voir aussi : trapèze comme section par un plan
1.4. Trapèzes comme sections planes du cube
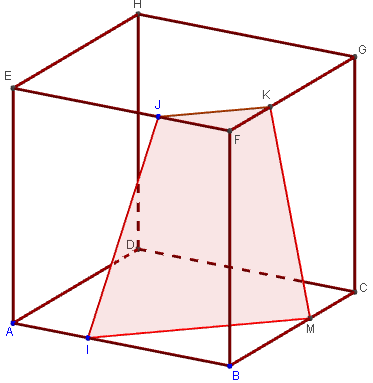
Trapèze lorsque la section coupe l'arête [BC]
Section plane déterminée par trois points sur des arêtes du cube
Créer les points I et J sur deux arêtes parallèles
[AB], et [EF], placer un troisième point K sur
[FG], arête ayant le sommet F en commun avec [EF].
Comme les faces (ABCD) et (EFGH) du cube
sont parallèles, le plan (IJK) coupe le plan
(ABC) suivant une parallèle (d) à (JK).
Figure ci-dessus :
La droite (d) coupe (BC) en M, point
d'intersection du plan (IJK) avec (BC).
Si le pont M est sur le segment [BC]
la section est alors un trapèze.
Tracer le trapèze IJKM.
Trapèze lorsque la section coupe l'arête [CD]
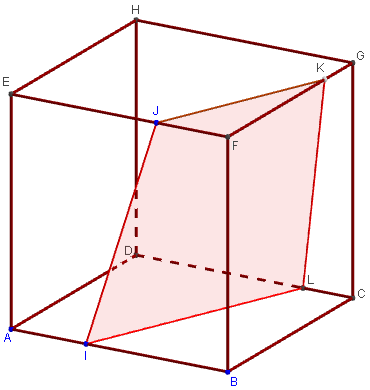
La droite (d) coupe (CD) en L, point d'intersection
du plan (IJK) avec le segment [CD].
Tracer le trapèze IJKL.
Figure 3D dans GeoGebraTube :
deux trapèzes comme section plane du cube
1.5. Parallélogramme ou pentagone comme sections du cube
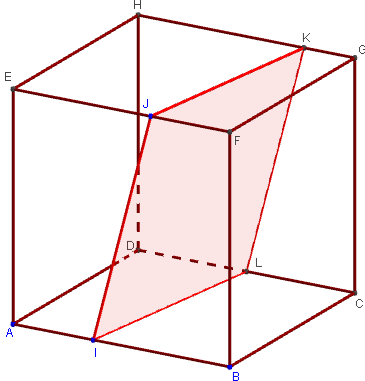
Section plane déterminée par trois points sur des arêtes parallèles
Comme pour la figure précédente, mais avec le point K sur [HG] :
créer les points variables I, J et K sur les trois arêtes
parallèles [AB], [EF] et [HG].
Construction des autres sommets de la section
Cas où la section coupe la quatrième arête [CD]
Trouver le point L intersection du plan (IJK) avec le
segment [CD]. Tracer le parallélogramme IJKL.
Déplacer les points I, J ou K pour faire apparaître
le plus explicitement possible ce parallélogramme.
Cas où la section ne coupe pas le segment [CD]
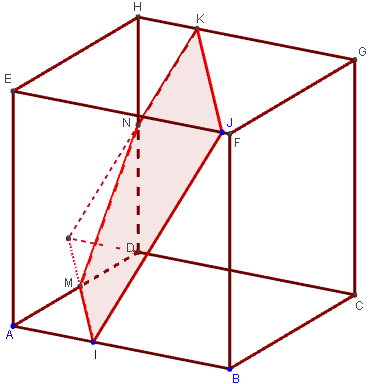
Dans le cas où le point L intersection du plan (IJK)
avec la droite (CD) est à l'extérieur du segment
[CD], trouver l'intersection du plan (IJK) avec une
autre face du cube, par exemple avec la face ADHE si le point
L est sur la droite (CD) du côté de D.
Trouver l'intersection M du plan (IJK) avec [AD] et N avec [DH].
Tracer le pentagone IJKNM, ayant deux côtés parallèles [JK] et [IM].
Figure 3D dans GeoGebraTube :
parallélogramme ou pentagone comme sections planes du cube
1.6. Pentagone - problème de Bergson
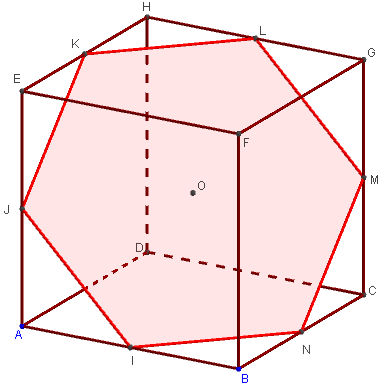
I est le milieu de [AB], J le milieu de [AE] et K le milieu de [EH].
Trouver la section plane du cube par le plan (IJK).
Figure 3D dans GeoGebraTube :
hexagone de Bergson comme section plane du cube
Voir le problème de Bergson au lycée.
B. Sections planes d'un parallélépipède rectangle
Section par un plan parallèle à la face AEHD.
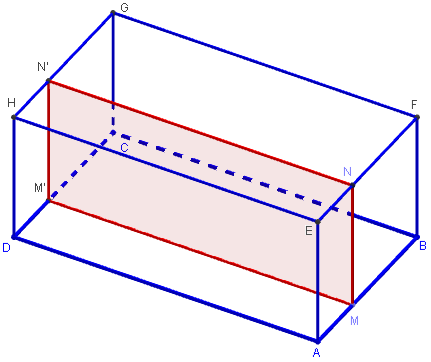
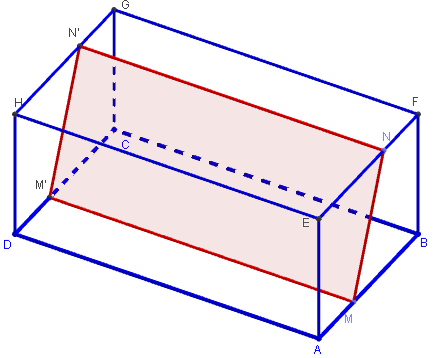
Section par un plan parallèle à l'arête [AD].
Figure 3D dans GeoGebraTube :
section plane d'un parallélépipède rectangle
La section d'un parallélépipède rectangle (ou d'un
cube) par un plan parallèle à une face ou une arête
est un rectangle, dans le cas où le plan est parallèle
à une face, la section est un rectangle ayant les
mêmes dimensions que cette face.
Travaux Pratiques 2
Sections de pyramide
2.1. Section d'une pyramide parallèle à la base
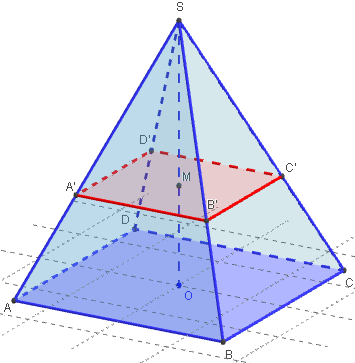
Sur la hauteur [OS] placer un point variable M.
Créer le plan (p) parallèle à la base de la pyramide,
passant par le point M.
Avec l'icône « intersection de deux surfaces »,
créer la section plane intersections du plan (p) avec
la pyramide et renommer A’, B’, C’et D’ les
sommets du carré situés sur les arêtes de la pyramide.
Quelle est la nature du solide SA’B’C’D’ ?
Cas général :
section plane d'une pyramide en seconde
2.2. Tronc de pyramide
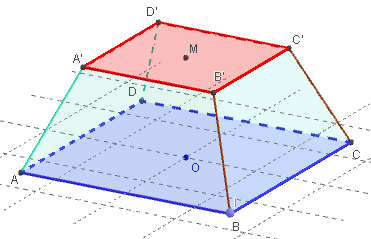
Après avoir tracé la section carrée A’B’C’D’,
effacer la grande pyramide,
créer les quatre
faces latérales : trapèzes ABB’A’…
Le solide ABCDA’B’C’D’ est un tronc de pyramide.
Figure 3D dans GeoGebraTube :
section plane et tronc d'une pyramide de base carrée
2.3. Volume d'un tronc de pyramide (ou d'un tronc de cône)
(hors programme)
Calculer le volume de la pyramide non tronquée,
puis en déduire le volume de la partie tronquée.
En appelant B l'aire de la grande base ABCD et b
l'aire de la petite base A’B’C’D’ et h la hauteur
du tronc, la formule du volume du tronc est alors :
V = 
[B + 
+ b ].
Pour calculer le volume du tronc de pyramide de base carrée,
avec a et b comme longueur des côtés des carrés
les anciens Égyptiens utilisaient une méthode
revenant à l'emploi de la formule :
V = [a2 + ab + b2].
2.4. Pyramide gauche
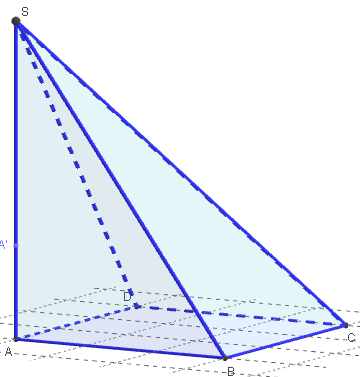
Recommencer avec une pyramide ABCDS de
base carrée ABCD, trirectangle en A, telle
que l'arête [AS] soit une hauteur de la pyramide.
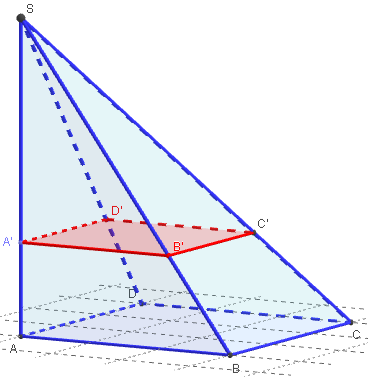
Placer le point variable A’ sur le segment [AS] et
tracer la section plane A’B’C’D’ de la pyramide
par le plan (p) passant par A’, parallèle à la base.
Figure 3D dans GeoGebraTube :
pyramide gauche de base carrée
Section plane d'une pyramide gauche
Travaux Pratiques 3
Section et tronc de tétraèdre - Solide composite
3.1. Section plane et tronc de tétraèdre
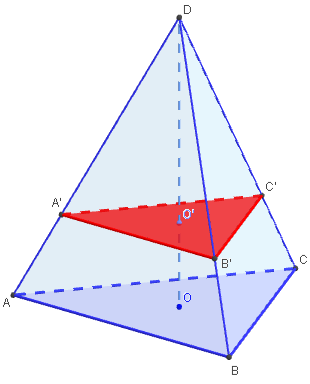
Section plane
À partir d'un point O ’ situé sur la hauteur [OD],
dessiner les traces (sur le tétraèdre) du plan
passant par O ’, parallèle au plan de base (ABC).
Créer le plan (p) parallèle à la base de la pyramide,
passant par le point O'.
Avec l'icône « intersection de deux surfaces », créer
la section plane intersections du plan (p) avec le un
tétraèdre et renommer A’, B’ et C’, les sommets du
triangle situés sur les arêtes du tétraèdre.
Figure 3D dans GeoGebraTube :
section plane et tronc d'un tétraèdre
Voir au lycée : section de tétraèdre par un plan
Tronc de tétraèdre
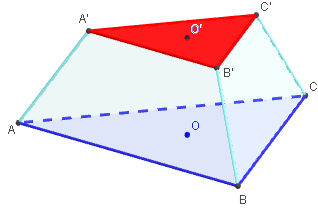
Après avoir tracé la section triangulaire A’B’C’,
effacer le grand tétraèdre,
créer les trois faces latérales : trapèzes ABB’A’…
Le solide ABCA’B’C’ est un tronc de tétraèdre polyèdre à 5 faces.
Si ABCD est un tétraèdre régulier,
le tétraèdre réduit A’B’C’D est-il régulier ?
3.2. Solide assemblage d'un cube et d'une pyramide
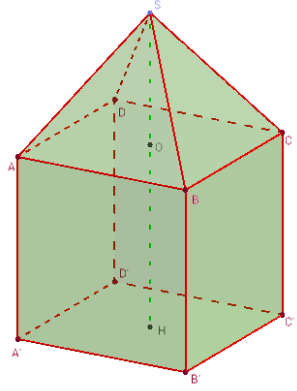
Lanterne : solide composite
Comment dessiner une pyramide de base carrée posée sur un cube ?
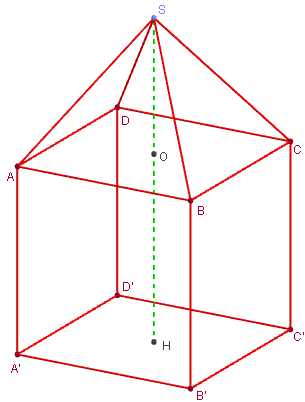
Charger la figure 3D de GeoGebraTube : cube
Tracer la médiatrice d'une des faces du cube
(placer les points O au milieu de la face ABCD et
H au milieu
de la face A’B’C’D’, O et H sont les
« milieux de diagonales »).
Placer le point S sur cette médiatrice [HO)
et créer le solide : A’B’C’D’ABCDS.
Figure 3D dans GeoGebraTube : lanterne
4. Sections planes de solides de révolution
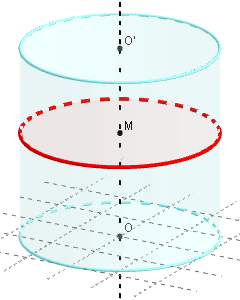
Cylindres dont les bases sont deux cercles de centres
O et O’ et rayon r.
L'axe (OO’) des cylindres est
perpendiculaire aux plans des cercles de base.
4.1. Cylindre - plan horizontal
Section par un plan perpendiculaire à l'axe (OO’) du
cylindre, passant par un point M du segment [OO’].
La section est un cercle de centre M.
Figure 3D dans GeoGebraTube :
section de cylindre
Terminale S : Volume d'un tronc de cylindre
4.2. Cylindre - plan vertical
Ancienne version GéoSpace,
adaptation à GeoGebra en projet
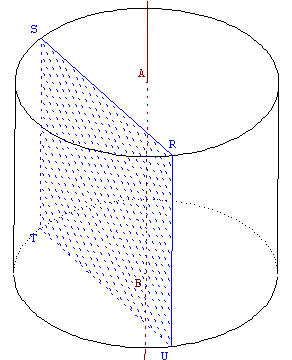
Section par un plan parallèle à l'axe du cylindre, passant
par les points R et S, situés sur un des cercles de base.
La section est le rectangle RSTU.
Indication : la translation de vecteur 
transforme le
cercle de base (c) de centre A en (c’), cercle de base de
centre B.
Les points R et S en U et T : RSTU est un parallélogramme.
Les côtés [RU] et [ST], parallèles à l'axe (AB) sont
perpendiculaires à la base :
un angle droit, d'où un rectangle.
4.3. Cône de révolution
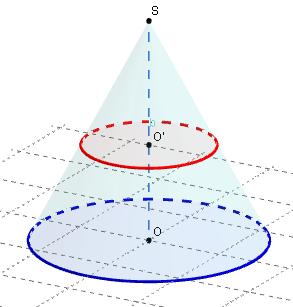
Section plane d'un cône par un plan parallèle à la base
La figure représente un cône de révolution.
L'axe du cône est (OS). Sa hauteur OS sera notée h.
O est le centre du cercle de base (c) de rayon r.
Soit O’ un point de [OS]. On coupe ce cône par un
plan (P) perpendiculaire à son axe en O’.
L'ensemble des points qui sont à la fois dans le plan
et sur la surface latérale du cône est un cercle (c’)
de centre O’ et de rayon r’.
Figure 3D dans GeoGebraTube : section de cône
4.4. Sphère
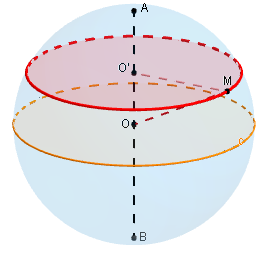
(S) est une sphère de centre O et de rayon R, (P) un plan.
O’ est le pied de la perpendiculaire à (P) menée par O.
OO’ est la distance de O à O’, notée d.
On suppose que M est un point commun au plan
et à la sphère et on note O’M = r.
Dans le triangle OO’M, rectangle en O’,
de la propriété de Pythagore :
O’M2 + OO’2 = OM2,
on déduit r2 = R2 - d2.
Si d < R, l'ensemble des points d'intersection entre la
sphère (S) et un plan (P) situé à une distance d de O
est le cercle, du plan (P), de centre H
et de rayon r = 
.
Si d = R, le plan est tangent à la sphère en O’.
Si d > R, le plan ne coupe pas la sphère.
Figure 3D dans GeoGebraTube :
section de sphère
Table des matières
…Avec GeoGebra 3D dans d'autres pages du site
Mode d'emploi GeoGebra 3D
Mobile friendly
sur ordinateur, cette page pour grand écran
Copyright 2014 - © Patrice Debart
…Avec GeoGebra 3D dans d'autres pages du site
Sections planes du cube : Cube en 2nde
Intersection d'un plan et d'un cube
Pyramide : le cours - Partition d'un cube en trois ou six pyramides
Intersection de plans autour d'une pyramide
Page no 11, adaptée à GeoGebra 3D le 17/12/2014