Descartes et les Mathématiques
L'espace en cinquième avec GeoGebra 3D
Prismes droits, cylindres de révolution : patrons, représentation en perspective.
Sommaire
1. Prisme de base triangulaire
2. Prisme dont la base est un parallélogramme
3. Cylindre
4. Une maison
5. Cube tronqué
Prisme - Définition
Un prisme est un solide ayant deux bases qui sont des polygones. Ces polygones situés dans des plans parallèles sont isométriques.
Les arêtes du prisme sont des droites parallèles. Les faces latérales sont des parallélogrammes.
Pour un prisme droit, les arêtes sont perpendiculaires aux plans des bases et les faces latérales sont des rectangles.
Leur longueur est alors la hauteur du prisme, égale à la distance entre les deux bases.
1. Prisme de base triangulaire
1.a. Prisme droit de base un triangle
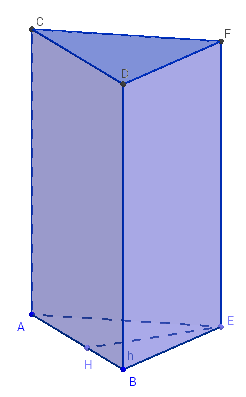
Prisme vertical
ABC et DEF sont les bases du prisme droit ABCDEF.
Les faces latérales ABED, BCFE et CADF sont des rectangles.
Les arêtes [AD], [BE] et [CF] sont perpendiculaires aux plans des bases. Leur longueur est la hauteur du prisme, égale à la distance entre les deux bases.
Figure 3D dans GeoGebraTube : prisme vertical de base triangulaire
Volume du prisme droit
Volume = Aire de la base × hauteur
= B × h
= Aire(ABC) × AD.
Aire de la base triangulaire
Aire(ABC) = 
base × hauteur
Aire(ABC) = AB × CH.
Calcul du volume du prisme
Volume(ABCDEF) = AB × CH × AD.
Prisme horizontal
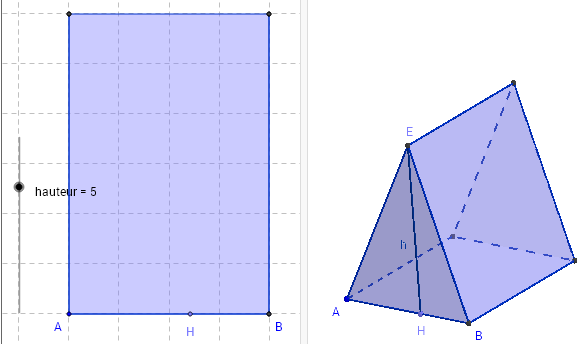
Base, hauteur
Il est difficile, pour les élèves, d'identifier base et hauteur, notions que l'on trouve aussi bien dans le prisme, que dans le triangle.
Dans le sens commun, comme dans la figure de gauche, la base ABC du prisme est horizontale et la hauteur [AD] est verticale.
En géométrie, ces objets sont indépendants de leur position. Par exemple, dans la figure ci-dessus la base ABC du prisme est verticale et la hauteur [AD] est horizontale.
Pour le calcul de l'aire du triangle ABC, dans la figure de gauche la hauteur [CH] est horizontale, on retrouve le langage courant, dans la figure ci-dessus, avec la base [AB] horizontale et la hauteur [CH] verticale.
Aire latérale
L'aire latérale d'un prisme droit est égale au périmètre de la base, multiplié par la hauteur :
(AB + BC + CA) × AD.
Figure 3D dans GeoGebraTube : prisme horizontal de base triangulaire
Figure 3D dans GeoGebraTube : patron de prisme horizontal de base triangulaire
Patron de prisme
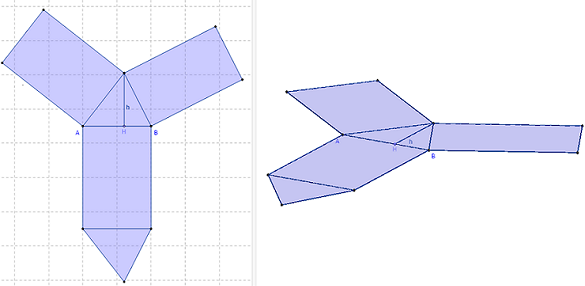
On obtient, parmi tous les patrons possibles, le patron choisi par le logiciel à partir de la base triangulaire, face principale ayant servi à sa construction.
Les autres faces s'articulent autour de cette face.
Avec GeoGebra le patron est développé autour d'une face triangulaire ABE et on ne peut pas le faire suivant la base horizontale ABCD.
Figure 3D dans GeoGebraTube : patron de prisme de base triangulaire dans le plan horizontal.
Prisme dont la base est un parallélogramme
2. Prisme de base rectangulaire
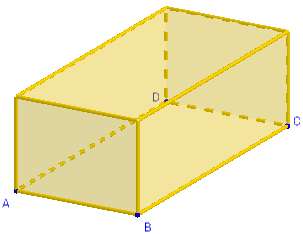
(Extrait de GeoGebra 3D en 6e)
Parallélépipède : polyèdre à six faces qui sont toutes des parallélogrammes. Les faces opposées sont égales et parallèles.
C'est un prisme dont la base est un parallélogramme.
Parallélépipède rectangle : polyèdre à six faces qui sont toutes des rectangles. C'est un prisme droit dont la base est un rectangle.
À l'école, le terme parallélépipède rectangle n'est pas exigible au cycle 2, on lui préférera celui de pavé droit.
Figure 3D dans GeoGebraTube : pavé droit
Voir : Patron du pavé droit
Calcul du volume du parallélépipède rectangle
Volume(ABCDEFGH) = Aire de la base × hauteur
= Aire(ABCD) × AE = AB × AD × AE.
Cas particulier : volume du cube de côté a
Volume(ABCDEFGH)
= Aire de la base × hauteur
= Aire(ABCD) × AE
= a2 × a = a3.
3. Cylindre de révolution
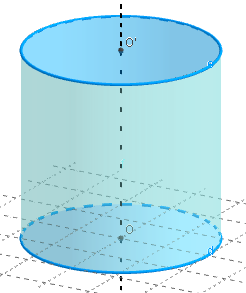
Pour ce cylindre, les bases sont deux cercles de centres O et O’ ; de rayons r.
L'axe (OO’) du cylindre est perpendiculaire aux plans des cercles de base.
Volume du cylindre
Pour un cercle de base de rayon r, l'aire de la base est πr2 ;
la longueur h de la hauteur [OO’] est égale à la distance entre les deux bases.
Volume = aire de la base × hauteur
Volume = B × h = πr2 × OO’ = πr2h.
Aire latérale
L'aire latérale d'un cylindre de révolution est égale au périmètre de la base multiplié par la hauteur :
2πr × OO’ = 2πrh.
Figure 3D dans GeoGebraTube : cylindre de révolution
4. Solide composite : une maison avec GeoGebra 3D
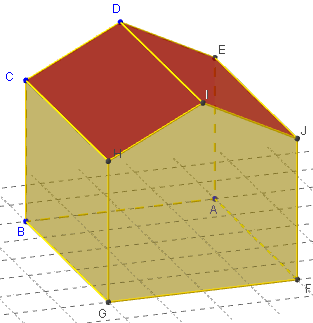
Une maison de poupée a la forme d'un parallélépipède rectangle, surmonté d'un prisme droit.
Calculer le volume de cette maison.
La longueur du parallélépipède est de 7 cm, sa largeur de 5 cm et sa hauteur de 4 cm.
La hauteur totale de cette maison est de 6 cm.
Le volume v est alors de 175 cm3.
Calcul du volume de la maison
Calculer le volume compris entre les murs et ajouter celui du toit :
Volume(ABCDEFGHIJ) = Volume(ABCDEFGH) + Volume(EFGHIJ)
Volume du parallélépipède rectangle :
Volume(ABCDEFGH)
= Aire(ABFE) × FG = AB × AE × FG = a × c × b.
Volume du prisme :
Volume(EFGHIJ) = Aire(FEI) × FG
= FE × (h-c) × FG = a × (h-c) × b.
Volume(ABCDEFGHIJ) = Aire(ABFE) × FG + Aire(FEI) × FG
= [ Aire(ABFE) + Aire(FEI) ] × FG.
Volume(ABCDEFGHIJ) = a × c × b + a × (h-c) × b = a × [ c + (h-c)] × b = a × (h+c) × b.
Effectivement, la maison est un prisme de base pentagonale ABFIE
et avec Aire(ABFE) + Aire(FEI) = Aire(ABFIE) on retrouve :
Volume(ABCDEFGHIJ) = Aire(ABFIE) × FG = Aire de la base × hauteur.
Figure 3D dans GeoGebraTube : maison
5. Cube tronqué
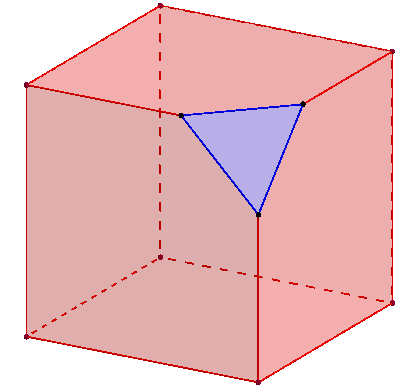
Cube au « coin coupé »
Polyèdre à 7 faces
On a coupé un « coin » du cube au tiers des arêtes par un plan perpendiculaire à une diagonale du cube.
Figures 3D dans GeoGebraTube : cube au coin coupé,
Voir : « coin de cube » ; « cube fortement tronqué » lorsque les côtés du « coin » sont trois des diagonales de faces du cube.
Voir aussi les arts conceptuels de Sol LeWitt : wall drawings
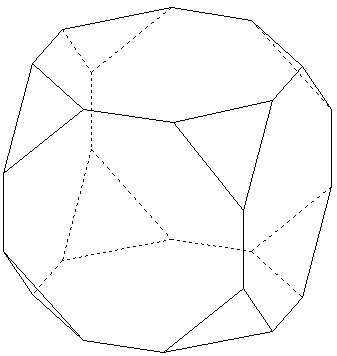
Cube aux huit « coins coupés »
Figure GéoSpace
Représenter en perspective le solide obtenu en coupant, de même manière, les huit « coins » d'un cube.
Les côtés des triangles sont de longueur inférieure à la moitié de la longueur d'une diagonale d'une des faces du cube.
Il possède 6 faces octogonales, 8 faces triangulaires (triangles équilatéraux), 24 sommets et 36 arêtes.
Ce solide est un cube tronqué ou hexaèdre tronqué lorsque les faces octogonales sont régulières.
Le cube tronqué est un des 13 solides d'Archimède.
Figures 3D de Philippe Vesvre dans GeoGebraTube : cube tronqué
Solide d'Archimède (287-212 avant J.-C.) : Polyèdre semi-régulier dont les faces sont des polygones réguliers, ceux-ci pouvant être différents, mais disposés dans le même ordre autour de chaque sommet. Le cube tronqué est un des 13 solides d'Archimède.
Table des matières
Les figures de cette page avec GéoSpace
…Avec GeoGebra 3D dans d'autres pages du site
GeoGebra 3D en 4e Pyramide
Mode d'emploi GeoGebra 3D
Google friendly
Page no 94, adaptée à GeoGebra 3D le 4/12/2014