Descartes et les Mathématiques
Sections de tétraèdre par un plan
Intersection d'un plan avec les faces ou avec le plan de base d'un tétraèdre, avec GeoGebra 3D.
Sommaire
1. Triangle comme section d'un tétraèdre
2. Parallélogramme comme section d'un tétraèdre
3. Quadrilatère comme section d'un tétraèdre par un plan
4. Trapèze comme section d'un tétraèdre
5. Trois points sur les faces d'un tétraèdre
Programme de 1ère S (2009)
La géométrie dans l'espace est source de situations permettant de mettre en œuvre de nouveaux outils de l'analyse ou de la géométrie plane, notamment dans des problèmes d'optimisation.
Malgré cet entête, la géométrie dans l'espace a disparu du nouveau programme !
Sections planes : En général, dans les exercices ci-dessous, nous décrivons la construction point par point des sections, en explicitant les divers cas particuliers.
Avec GeoGebra 3D, on crée la section plane avec l'outil intersection de surfaces.
Avec la souris, il n'est pas facile de sélectionner tout le tétraèdre et souvent on ne sélectionne qu'une seule face.
On a intérêt à sélectionner le plan, puis dans le menu algèbre, sélectionner le tétraèdre a ;
ou bien, en bas de l'écran, saisir d=IntersectionChemins[Plan[A,B,C], a]
Dès que l'on tape d=Int le logiciel propose la syntaxe précise :
d=IntersectionChemins[<Plan>, <Polygone>]
Remplacer les <...> par le nom du plan et celui du tétraèdre.
1. Triangle comme section plane d'un tétraèdre
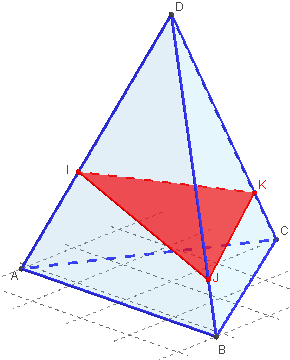
Coupe d'un tétraèdre par un plan
Soit trois points I, J et K sur les arêtes concourantes au sommet D d'un tétraèdre
I est un point de [AB], J de [AC] et K de [AD].
a. Section plane
Créer la section du tétraèdre par le plan (IJK).
Déplacer les points I, J et K et observer la section obtenue.
Figure 3D dans GeoGebraTube : triangle comme section plane d'un tétraèdre
Intersections d'un plan avec des arêtes
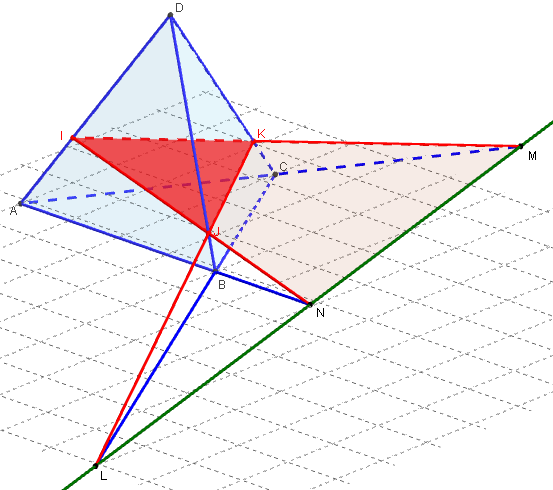
b. Trouver l'intersection du plan (IJK) avec le plan de base (ABC).
Dans la face latérale ABD, étudier l'intersection des droites (IJ) et (AB).
On suppose que ces deux droites ne sont pas parallèles, leur point N d'intersection appartient aux plans (IJK) et (BCD).
De même dans la face BCD, étudier l'intersection des droites (JK) et (BC). Si ces deux droites sont parallèles, voir le cas particulier ci-dessous, sinon leur point L d'intersection appartient aux plans (IJK) et (ABC).
On en déduit alors que le plan (IJK) coupe le plan horizontal (ABC) suivant la droite (LN).
Enfin, trouvez le point M d'intersection des droites (KI) et (AC) situé dans la face ACD.
En général, ces deux droites sont sécantes en M.
Règle d'incidence : Pour prouver l'alignement de trois points dans l'espace, on peut montrer que ces trois points sont communs à deux plans sécants, ils sont alors sur la droite d'intersection de ces deux plans.
Les points L, M et N, lorsque qu'ils existent, sont alignés. Ces points appartiennent à la droite d'intersection des plans (IJK) et (ABC).
1.b.Section par un plan parallèle à une arête
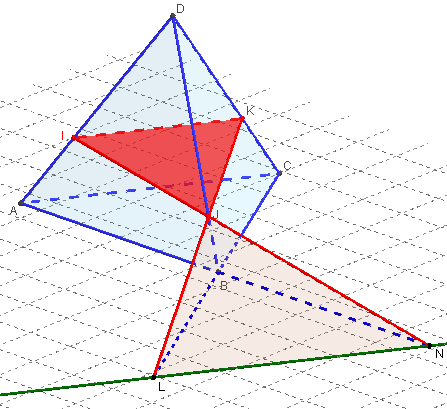
Soit trois points sur trois arêtes concourantes au même sommet D d'un tétraèdre ABCD, tels que la section déterminée par ces trois points ait un côté parallèle à un des côtés de la base du tétraèdre.
Par exemple :étudier l'intersection du plan de cette section contenant la droite (IK), parallèle l'arête (AD).
Si le point J est dans un plan parallèle à la base ABC, voir section plane d'un tétraèdre par un plan parallèle à la base ;
Sinon
L est le point d'intersection des droites (JK) et (BC),
N est le point d'intersection des droites (IJ) et (AB).
(LN) est la droite d'intersection des plans (IJK) et (ABC).
D'après le théorème du toit, (LN) est parallèle à (AC).
Figure 3D dans GeoGebraTube : section du tétraèdre par un plan parallèle à une arrête
2. Parallélogramme section d'un plan parallèle à deux arêtes
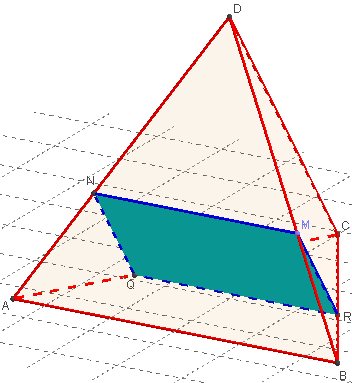
Tracer la section d'un tétraèdre
Construction
ABCD est tétraèdre.
M est un point de l'arête [AC].
Construire la section du tétraèdre par le plan (p) passant par M et parallèle aux arêtes [AB] et [CD].
Montrer que la section plane MNQR est un parallélogramme.
Construction avec GeoGebra 3D
Tracer la droite d1 passant par M parallèle à (AB), qui coupe (AD) en N,
et la droite d2 passant par M parallèle à (CD), coupe (BC) en R.
L'instruction p = Plan[d1, d2] crée le plan (p) contenant les deux lignes données.
(p) coupe (AC) en Q.
Démonstration
(AB) est parallèle à d1 = (MN). Par le théorème du toit (QR), intersection des plans (p) et (ABC), est parallèle à (AB).
Donc (MN)//(QR).
De même (MR) //(CD) est parallèle à (NQ).
MNQR est un parallélogramme.
Figure 3D dans GeoGebraTube : parallélogramme comme section du tétraèdre
2.b. Deux parallélogrammes, sections parallèles à 2 arêtes
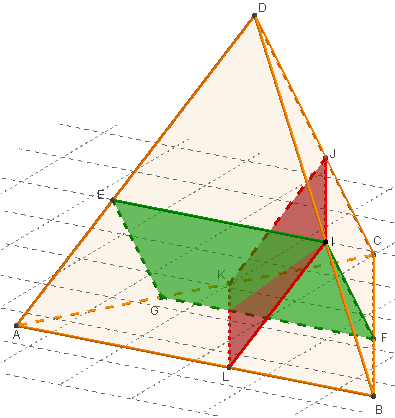
Réciproque : parallélogramme comme section d'un tétraèdre
ABCD est un tétraèdre non aplati.
Montrer que si l'intersection d'un plan et d'un tétraèdre est un parallélogramme, les côtés du parallélogramme sont parallèles à des côtés du tétraèdre.
Si la section IJKL est un parallélogramme, les droites (IJ) et (LK) sont parallèles, la droite (IJ) est contenue dans le plan (ABC), (LK) contenue dans le plan (DBC). Ces plans se coupent selon la droite (BC), d'après le théorème du toit les droites (IJ) et (LK) sont parallèles à (BC).
De même, les droites (IL) et (JK) sont parallèles à (AD).
La section plane est parallèle à deux arêtes du tétraèdre.
Deux parallélogrammes, sections planes menées à partir d'un sommet I
Soit I un point de l'arête [BD] d'un tétraèdre ABCD.
Par I on peut tracer deux couples de droites d1 et d2 parallèles aux arêtes opposées (BC) et (AD), puis d3 et d4 parallèles aux arêtes opposées (AC) et (BD).
Les plans passants par I, plan p contenant les droites d1et d2 d'une part, puis d3 et d4 d'autre part, coupent le tétraèdre suivant deux parallélogrammes de sommet I.
Figure 3D dans GeoGebraTube : 2 parallélogrammes sections planes du tétraèdre
2.c. Trois parallélogrammes, sections passant par un point
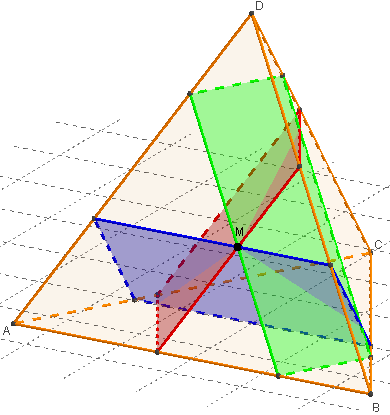
Par un point M d'une face non situé sur une arête du tétraèdre, on peut faire passer trois droites parallèles aux côtés de cette face.
Les sections des trois plans contenant ces droites et parallèles aux arêtes opposées sont des parallélogrammes contenant M.
Figure 3D dans GeoGebraTube : trois parallélogrammes sections planes du tétraèdre
Point M non situé sur les arêtes du tétraèdre
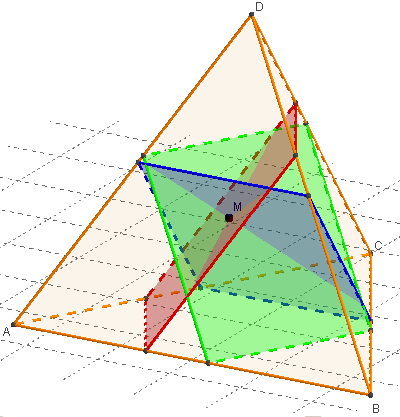
Pour un point M de l'espace non situé sur les arêtes du tétraèdre, il existe trois plans, passant par M, coupant le tétraèdre suivant des parallélogrammes.
Figure 3D dans GeoGebraTube : 3 parallélogrammes comme sections du tétraèdre
3. Quadrilatère section d'un tétraèdre
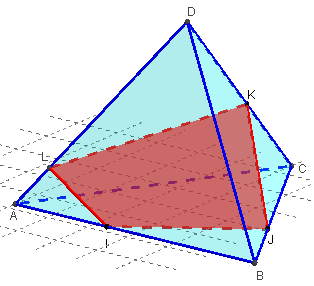
Section d'un tétraèdre par un plan déterminé par deux points sur deux arêtes concourantes et un troisième point sur une autre arête.
Sur deux arêtes du plan de base concourantes en B, on choisit un point I sur [AB] et J sur [BC] et à l'extérieur du plan, sur un arête ne contenant pas B, on a le point K sur [CD].
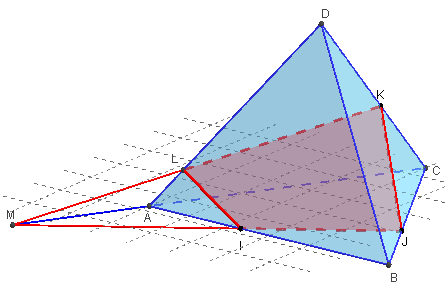
Quadrilatère comme section d'un tétraèdre par (IJK).
3.b. Construction du quadrilatère
Section plane de tétraèdre
Si (IJ) n'est pas parallèle à (AC), ces deux droites se coupent en M.
La droite (MK) coupe [AD] en L.
Le quadrilatère IJKL est la section du tétraèdre par le plan (IJK).
Voir ci-dessus le cas particulier du parallélogramme.
Figure 3D dans GeoGebraTube : quadrilatère comme section plane d'un tétraèdre
Section d'un tétraèdre par un plan déterminé par deux points sur deux arêtes concourantes et un troisième point sur la quatrième face ne contenant pas ces arêtes.
Figures 3D dans GeoGebraTube
Figure de base : trois points sur un tétraèdre
Réalisation : construction de la section plane d'un tétraèdre
4. Trapèze comme section plane
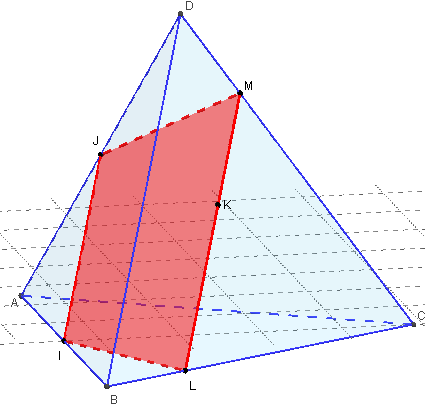
Sur un tétraèdre ABCD, soit I le milieu du segment [AB], J le milieu du segment [AD] et K un point de la face (BCD).
Construire la section du tétraèdre par le plan (IJK).
Solution :
(IJ) droite des milieux du triangle ABD est parallèle à (AB).
D'après le théorème du toit, l'intersection du plan (IJK) et du plan (BCD) est la droite parallèle à (BD) passant par K.
Cette droite rencontre (BC) en L et (CD) en M.
La section plane est le trapèze IJLM.
Figure 3D dans GeoGebraTube : trapèze comme section plane d'un tétraèdre
Variante
I est un point de [AB], J est le point d'intersection de [AD] avec la parallèle à (BD) passant par I, et K un point de la face (BCD).
Construire la section du tétraèdre par le plan (IJK).
5. Section passant par trois points I, J et K sur les faces
Si le plan (IJK) est parallèle au plan de base (BCD), la section est un triangle aux côtés parallèles à ceux du triangle ABC, contenant les trois points I, J K.
voir section plane et tronc d'un tétraèdre
Sinon :
a. Trouver l'intersection du plan (IJK) avec la base (ABC).
Utilisez les plans (DIK) et (DJK).
Montrez que le plan (IJK) coupe le plan horizontal (BCD) suivant une droite (QR).
b. Trouver l'intersection de la section plane avec les autres faces du tétraèdre.
Tracer le point d'intersection S de la droite (QR) avec (AB) et en déduit l'intersection du plan (IJK) avec la face (ABC).
Si le point S est entre A et B, la section est un quadrilatère, sinon lorsque S est à l'extérieur de [AB], on obtient une section triangulaire.
Figure 3D dans GeoGebraTube section déterminée par 3 points sur 3 faces d'un tétraèdre
6. Parallélogramme inscrit dans un tétraèdre
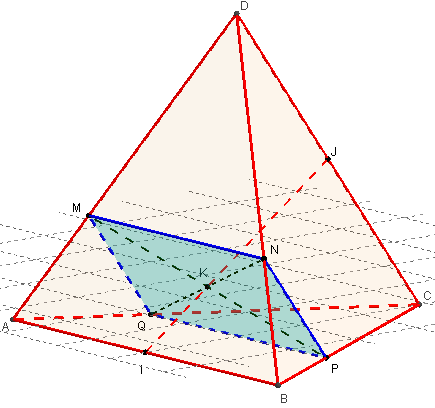
ABCD est un tétraèdre, I et J sont les milieux respectifs de [AC] et [BD]
8.a. Montrer l'égalité vectorielle 
+ 
= 2 
8.b. Soit k un réel donné dans l'intervalle ]0, 1[.
On définit les points M, N, P, Q par :
= k 
; 
= k ; 
= k 
; 
= k .
Montrer que MNPQ est un parallélogramme. Soit K son centre.
Montrer 
= k , donc que K appartient au segment [IJ].
Pour k = 
, on trouve que K, centre de gravité du tétraèdre, est le milieu des trois segments dont les extrémités sont les milieux des arêtes opposées.
8.c. Démontrer qu'étant donné un point K du segment [IJ], il existe un unique point N de [AD] et un unique point Q de [BC] tels que K soit le milieu de [NQ].
Figure 3D dans GeoGebraTube : parallélogramme dans un tétraèdre
Voir ce problème à l'oral du Capes
7. Projection orthogonale
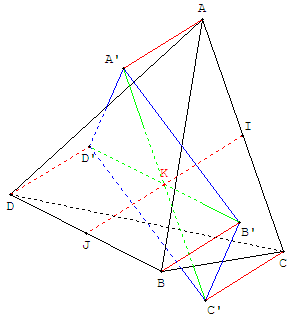
Ancienne version GéoSpace, adaptation à GeoGebra en cours
Montrer qu'un tétraèdre se projette orthogonalement sur un plan suivant un parallélogramme si et seulement s'il admet deux arêtes opposées dont les milieux sont sur une même perpendiculaire au plan de projection.
Indications
Les projections des deux arêtes opposées sont les diagonales du parallélogramme. Le point K, projection des milieux des arêtes, est le milieu des diagonales. Les diagonales se coupent en leur milieu, d'où parallélogramme.
Réciproquement, si la projection est un parallélogramme, la perpendiculaire au plan de projection passant par le milieu des diagonales intercepte les milieux des arêtes.
Télécharger la figure GéoSpace tet_4tp2.g3w
Table des matières
Les figures de cette page avec GéoSpace
…Avec GeoGebra 3D dans d'autres pages du site
Sections planes de cubes
3e : Sections planes d'un cube, d'un parallélépipède rectangle…
Lycée : Sections planes d'un cube,
Rétrolien (backlink)
Google friendly
Page no 89, réalisée le 9/1/2006
adaptée à GeoGebra 3D le 13/3/2015