René Descartes GeoGebra Descartes et les Mathématiques

La géométrie dans l'espace
en seconde

GeoGebra 3D au lycée :
règle d'incidence, alignement, intersection.

Sommaire

1. Orthogonalité dans l'espace : définitions

Théorème de la porte

Théorème du toit

Théorème des 3 perpendiculaires

2. Règle d'incidence : montrer un alignement

3. Traces d'un plan

1. Orthogonalité dans l'espace : définitions

1.a. Deux droites de l'espace sont perpendiculaires
lorsqu'elles sont sécantes et forment un angle droit
(dans le plan qui les contient toutes deux).

Deux droites de l'espace sont orthogonales lorsque
leurs parallèles respectives menées par un point
quelconque de l'espace sont perpendiculaires.

Avec GeoGebra 3D, créer une vue avec un
plan de face contenant une des droites pour
visualiser l'orthogonalité.

1.b. Théorème de la porte

geogebra 3d - théorème de la porte - copyright Patrice Debart 2016

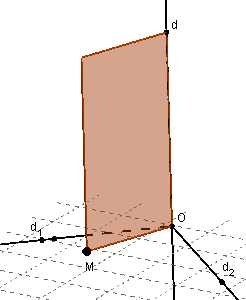
Une droite est orthogonale à un plan si et seulement si elle
est orthogonale à deux droites sécantes distinctes de ce plan.

Truc du menuisier : la droite (d), perpendiculaire aux
droites (d₁) et (d₂) sécantes en O, est perpendiculaire au
plan (p). La porte (p₁) tourne alors normalement autour de (d).

Figure 3D dans GeoGebraTube : théorème de la porte

Théorème : une droite perpendiculaire à deux droites
sécantes distinctes d'un plan est orthogonale à ce plan
(ces deux droites sont sécantes au point d'intersection
de la droite orthogonale et du plan).

Propriété : une droite orthogonale à un plan
est orthogonale à toutes les droites de ce plan.

Remarque : pour démontrer que deux droites sont
orthogonales, il suffit de démontrer que l'une des
droites appartient à un plan orthogonal à l'autre.

1.c. Théorème du toit

Le théorème du toit énonce une propriété de parallélisme pour l'intersection de deux plans sécants dans l'espace.

geogebra 3d - théorème du toit - copyright Patrice Debart 2016

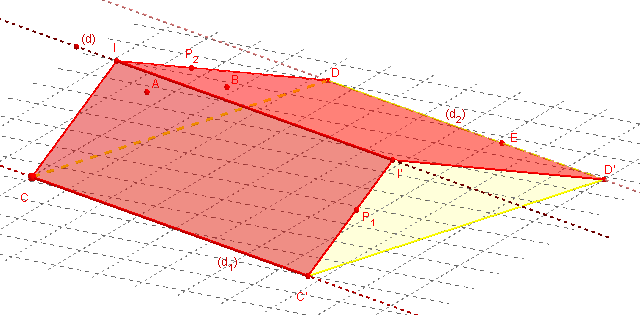
Si on a :
• deux droites parallèles d₁ et d₂,
• un plan P₁ contenant d₁,
• un plan P₂ contenant d₂,
alors la droite d d'intersection des deux plans P₁ et P₂,
si elle existe, est parallèle aux droites d₁ et d₂.

Figure 3D dans GeoGebraTube : théorème du toit

Voir : intersection de plans

WikiPédia : théorème du toit

1.d. Prisme droit de base un trapèze

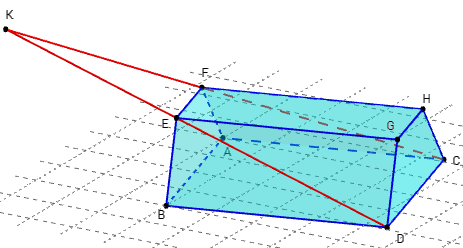
Diagonales des faces non parallèles

ABCDEFGH est un prisme droit de base le trapèze ABEF,
avec (AB)//(EF) et EF < AB.

Que peut-on dire des diagonales (DE) et (CF)
des faces ADHE et BCGF non parallèles ?

Figure 3D dans GeoGebraTube :
diagonales d'un prisme de base un trapèze

Illustration du théorème du toit

geogebra 3d - diagonales des faces et faitiere - copyright Patrice Debart 2015

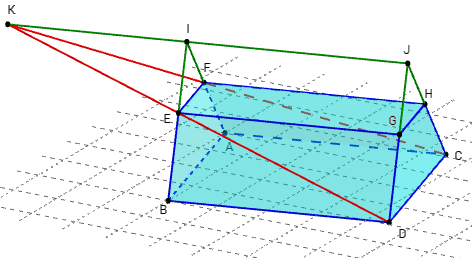
CDHG est un trapèze, avec (CD)//(GH),
EFGH est un rectangle, donc (GH)//(FE),
d'où (CD)//(FE), CDEF est un trapèze.
La droite (EF) est contenue dans le plan (CDE).
Les droites (DE) et (CF) sont coplanaires et donc concourantes en K.

Soit I et J les points d'intersection des côtés non parallèles des trapèzes.
Les plans (ADHE) et (BCGF) ont pour intersection la droite (IJ).
D'après le théorème du toit, (IJ) est parallèle à (AD) et (BC).

Le point K, contenu dans ces deux plans, est situé sur (IJ).

1.e. Théorème des trois perpendiculaires

geogebra 3d - 3 perpendiculaires - copyright Patrice Debart 2015

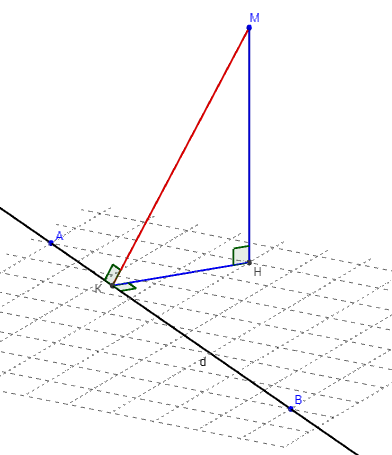
Soit (d) est une droite contenue dans un plan (p) et M un point de l'espace.

Si H est le projeté orthogonal de M sur (p) et K est le projeté
orthogonal de H sur (d), alors K est le projeté orthogonal de M sur (d).

Indication

La droite (MH) est orthogonale à (d) car elle est orthogonale
au plan (p) qui contient la droite (d). (HK) est orthogonale à
(d) par définition du point K.
Le plan (MHK) est donc orthogonal à (d) car il contient deux
droites sécantes orthogonales à (d).
Par suite, (d) est orthogonale à toute droite de (MHK)
et en particulier à (MK) ce qui prouve que K est le projeté
orthogonal de M sur (d).

Figure 3D dans GeoGebraTube : théorème des trois perpendiculaires

2. Règle d'incidence

geogebra 3d - règle d'incidence - copyright Patrice Debart 2015

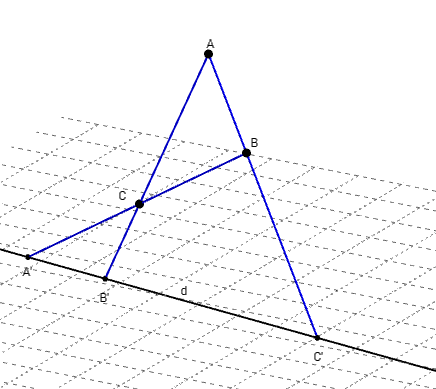
2.a. Pour montrer l'alignement de trois points de l'espace,
on peut montrer que ces trois points sont communs à deux
plans sécants, ils sont alors sur la droite d'intersection de ces deux plans.

Avec GeoGebra, soit (p) le plan horizontal planxOy.

A, B et C sont trois points non alignés n'appartenant pas à ce plan (p).
La droite (AB) coupe le plan (p) en C’,
la droite (AC) coupe le plan (p) en B’,
la droite (BC) coupe le plan (p) en A’.

Les points A’, B’ et C’ sont alignés.

En effet, ils appartiennent à la droite (d) d'intersection
des deux plans sécants (ABC) et (p).

Figure 3D dans GeoGebraTube : règle d'incidence

2.b. Montrer un alignement

geogebra 3d - prouver un alignement - copyright Patrice Debart 2015

Dans l'espace, soit trois demi-droites distinctes (d₁), (d₂),
(d₃) d'origine O. Sur chaque demi-droite on place deux
points : A₁ et B₁ sur (d₁) ; A₂ et B₂ sur (d₂) ; A₃ et B₃ sur (d₃).

Les droites (A₁A₂) et (B₁B₂) se coupent en I, (A₂A₃) et (B₂B₃)
en J et (A₁A₃) et (B₁B₃) en K

Que peut-on dire des points I, J et K ?

Indication

Considérer l'intersection des plans (A₁A₂A₃) et (B₁B₂B₃).

Les trois points I, J et K sont communs à deux plans sécants
(A₁A₂A₃) et (B₁B₂B₃), ils sont alignés sur la droite
d'intersection de ces deux plans.

Étudier les situations de parallélisme : (A₁A₂) // (B₁B₂) par exemple.

Figure 3D dans GeoGebraTube :
montrer un alignement dans l'espace

2.c. Lieux et point fixe

geogebra 3d - lieu géométrique dans l'espace - point fixe - copyright Patrice Debart 2015

A, B, P et P’ sont quatre points d'un plan (p),
les droites (AP) et (BP’) n'étant pas parallèles.

Selon la figure ci-dessus, sur la demi-droite (d) passant par le
point P, perpendiculaire au plan (p), on place un point M variable.

Le plan (ABM) coupe la demi-droite (d’),
perpendiculaire au plan (p), passant par P’, au point M’.

Les droites (AM) et (BM’) se coupent en I, et (AM’) et (BM) en J.

Lorsque l'on déplace le point M, quel est le lieu géométrique de I ? de J ?
Montrer que la droite (IJ) passe par un point fixe.

Figure 3D dans GeoGebraTube :
lieux et point fixe dans l'espace

3. Traces d'un plan

geogebra 3d - plan en perspective - copyright Patrice Debart 2015

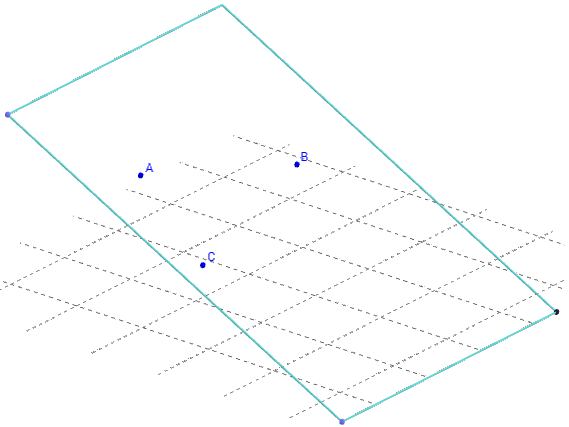
Tracer un plan en perspective

Comment faire un plan avec GeoGebra 3D

Pour représenter un plan, placer trois points dans ce plan,
compléter le parallélogramme formé par ces trois points
et tracer trois des côtés qui représentent des bords en perspective.

Figure 3D dans GeoGebraTube :
tracer un plan en perspective

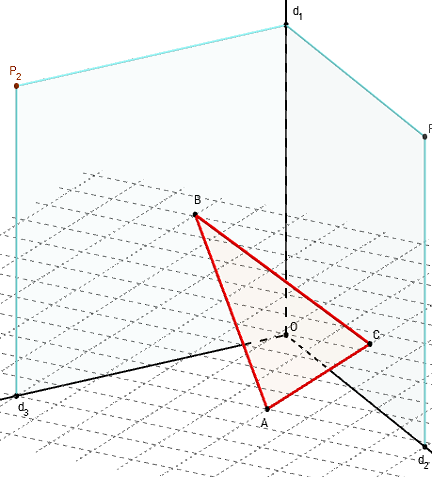
Trois plans sécants (p₁), (p₂) et (p₃) se coupent en O.
La droite (d₁) est l'intersection des plans (p₂) et (p₃),
(d₂) est l'intersection des plans (p₁) et (p₃),
(d₃) est l'intersection des plans (p₁) et (p₂).

Trois points distincts A, B et C sont dans les plans (p₁), (p₂) et (p₃).

Trouver les traces du plan (ABC) sur chacun des trois plans.

Figure 3D dans GeoGebraTube : traces d'un plan

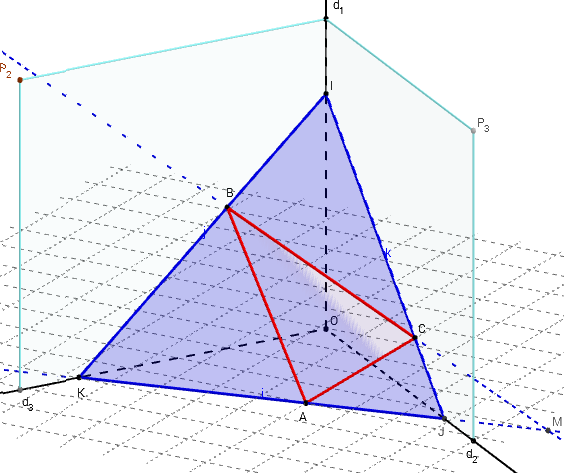
Si (BC) est parallèle au plan (p₁), la trace dans (p₁)
est la parallèle à (BC) passant par A, sinon la droite
(BC) coupe le plan (p₁) en M et la trace sur (p₁) est la droite (AM).

La droite (AM) coupe éventuellement (d₃) en I et (d₂) en J.
Les traces sont alors les droites (IB) et (JC) ;
en général, la trace du plan (ABC) est le triangle IJK.

Dans les cas particuliers, utiliser des parallèles
passant par des sommets du triangle ABC.