Géométrie du triangle
Droites remarquables du triangle
Cercles inscrit et exinscrits d'un triangle,
point de Feuerbach dans un triangle rectangle
Vingt-quatre points sur l'axe orthique
|
Géométrie du cercle
Puissance d'un point par rapport à un cercle
Trois cercles égaux tangents intérieurement à un triangle
Inversion de cercle
|
|
 Distance minimale dans un triangle
Échelle contre un mur
Parabole - Hyperbole
|
René Descartes (bac + 2)
Figures du problème de Pappus
Note sur le problème de Pappus
|
Figure géométrique
Beaucoup de problèmes de géométrie peuvent se traduire sous la forme d'existence et de construction d'une figure géométrique.
Résoudre un problème avec GeoGebra c'est transformer la description implicite d'une figure concrète en une description explicite codée avec les objets de la géométrie dynamique.
Le passage du concret aux algorithmes abstraits de la géométrie dynamique est le cœur de l’activité mathématique.
L'utilisation de GeoGebra permet de trouver les propriétés d’invariance d'une figure et de passer du numérique aux mathématiques.
Ce codage ludique permet de réconcilier l'enseignement avec la difficile géométrie.
 Faire de la géométrie dynamique avec GeoGebra
GeoGebra est une contraction de « geometry » et de « algebra ».
C'est un logiciel de géométrie dynamique qui permet de créer des objets géométriques dans la fenêtre graphique, mais aussi de travailler sur les grandeurs associées dans la fenêtre algébrique.
Tous les objets graphiques créés sont nommés automatiquement, mais il est facile de les renommer.
Il y a alors automatiquement dans la fenêtre algébrique : les coordonnées pour un point ou un vecteur ; l'équation pour une droite, un cercle ou une conique ; la longueur pour un segment…
Avec la ligne de commande, il est aussi possible de créer une expression qui sera insérée dans la fenêtre algébrique et qui créera un objet géométrique.
L'interface est d'une grande clarté et assez intuitive (un point créé à l'intersection de deux objets appartiendra à ces deux objets). Chaque action donnera, de façon transparente, un objet graphique et une expression dans la fenêtre algébrique.
Les objets créés sont facilement modifiables et, à partir de ces objets, il possible de créer des objets dépendants comme parallèles, perpendiculaires, médiatrices, bissectrices, lieux de points…
La figure peut aussi s'exporter dans divers formats :
• en « .eps », pour insertion dans un document LaTex,
• en « .png », pour inclure la figure statique dans un traitement de texte ou une page Internet,
• en image vectorielle « .svg », pour exportation (format peu utilisable dans Windows).
GeoGebra (Google ou GéoPlan) sont aussi des grapheurs :
en tapant x^2 + 2x - 3 dans la ligne de commande du bas de l'écran, la fonction s'affiche !
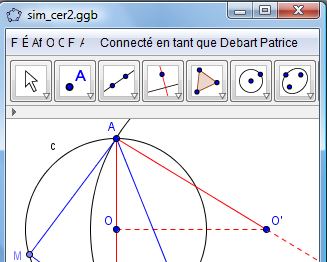
Figure ci-contre : conique d'Euler
Figures interactives dans GeoGebraTube : ellipse d'Euler
Ellipse d'Euler et centre du cercle d'Euler
|
|
Les fichiers ".ggb" sont maintenant moins fonctionnels et ne peuvent plus être téléchargés.
Les anciennes versions java ggbApplet sont encore actives, avec quelques bugs,
mais cette interactivité n'est plus possible depuis la version 4.4. de GeoGebra.
Téléverser dans GeoGebraTube
Depuis la version 4.3, il n'est plus possible d'exporter une feuille de travail dynamique en page web.
Maintenant il faut sauvegarder les figures dans GeoGebraTube. C'est la seule possibilité de sauvegarde pour les tablettes.
Les figures sont alors disponibles sur toutes les plateformes : pc, tablettes et smartphone.
La version 5.0 de GeoGebra PC ou tablette permet d'accéder directement à ces fichiers (Menu Fichier > ouvrir depuis GeoGebraTube > rechercher…
Cliquer sur le crayon, : l'icône GeoGebra correspond au navigateur) .
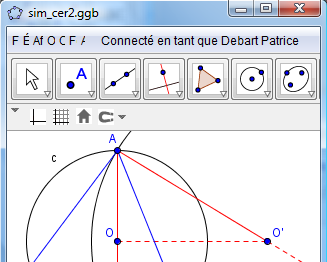
Pour cela, régler la taille de la fenêtre de GeoGebra.
Si comme à gauche la «barre de menu » est affichée sous la « barre d'outils », la supprimer en cliquant à gauche sur l'« icône triangle » pour obtenir la figure réduite de droite.
Après avoir « menu fichier - partagé » la figure, décocher la case dimension de l'appliquette et régler la taille de la figure.
Optimiser les dimensions avec width de 600px à 950px et height à moins de 700px, en ajoutant 100px si l'on veut afficher « Barre d'outils » et « Champ de saisie ».
|
Information pour les autres enseignants
Cette information est visible dans la page de la ressource, mais pas sur la feuille de travail de l'apprenant.
On l'obtient en cliquant,en haut à droite de la page ressource, sur l'icône du menu contextuel (trois points), puis en choisissant « À propos ».
Je publie en ressource publique.
J'avais publié des doublons en partagé, mais Google ne tient pas compte des balises « rel="nofollow" » et référence ces fichiers, donc autant tout partager avec la communauté GGB ! |
|
Il est possible de télécharger de GeoGebra pour tablettes et smartphones.
Java n'est plus prérequis pour GeoGebra et les versions 5.046 pour tablettes sont maintenant disponibles pour les plateformes Windows, Androïd (Google) et IOS (Apple), à télécharger à partir de la page GeoGebra !
Remarque : sur l'Iphone avec Safari, il est maintenant possible de retrouver les figures dynamiques de GeoGebraTube.
Ces outils auraient pu être de vrais ordinateurs, mais pour des raisons commerciales, ils ont été bridés et l'usage de GeoGebra y est un casse-tête.
Avec peu de possibilités d'échange et de sauvegarde de documents, ces écrans ne peuvent être facilement utilisés dans l'éducation.
Les sauvegardes et chargement des figure se font uniquement en ligne sur GeoGebraTube.
À partir de l'écran d'accueil, faire une recherche de ressource.
La sélection réalisée, il est possible d'éditer la figure dans le logiciel
ou d'afficher la ressource dynamique de GeoGebraTube
|
Barycentre
Le barycentre des points pondérés (A, α) et (B, β) est donné par (αA + βB)/(α + β).
Dans GeoGebra, il n'existe pas de repère sur une droite, pour y placer un point, utiliser les coordonnées barycentriques
|
Alignement de trois points
Pour afficher un objet lorsque trois points A, B et C, dans cet ordre sont alignés, créer les segments nommés AB, BC et AC puis dans les propriétés avancées de l'objet, utiliser l'inégalité triangulaire AB + BC = AC pour remplir la ligne condition pour afficher l'objet en tenant compte des incertitudes de calcul :
AB + BC - AC < 0.01
|
Commandes script
SoitValeur : voir le script par actualisation d'une case à cocher pour afficher, en 3D, un tétraèdre régulier.
En projet
|
Exemples de figures dynamiques avec GeoGebraTube
|
 Le téléversement des figures sur GeoGebraTube est en cours et 300 documents ont été téléversés, ainsi que 80 nouvelles figures 3D de l'espace.
GeoGebraTube : Pdebart
Lorsque vous utilisez une figure, pensez à « liker » en cliquer l'icône 
|
GeoGebra Book :
– La géométrie du triangle
– La planche à clous comme géoplan
– Calculs et découpage d'aires
– Polygones réguliers
– Triangle orthique
|
|
Page Internet |
GeoGebraTube
|
|
Le parallélogramme de Sander |
Parallélogramme de Sander
|
|
Lieux géométriques au collège |
Lieu du transformé d'un point mobile sur un cercle
Lieu des transformés de deux points mobiles sur un cercle
Milieu entre les sommets de deux triangles équilatéraux
Aires entre deux triangles équilatéraux
Triangle maximum entre deux triangles équilatéraux
Carré mobile
Point variable dans un rectangle
|
|
Carré d'aire cinq fois plus petite
|
Carré d'aire cinq fois plus petite
|
|
Calcul d'aires par découpage
|
Deux carrés d'aire cinq fois plus petite
Octogone dans un carré
|
|
Géométrie du triangle - Droites remarquables
|
Droite de Gergonne
Médianes d'un triangle
Triangle médian
Médiatrices d'un triangle
Symétriques de l'orthocentre
Construire un triangle à partir de l'orthocentre
Cercle inscrit dans un triangle
Cercles inscrit et exinscrit
Cercle inscrit et trois cercles exinscrits
|
|
Droites remarquables du triangle (ménéliennes)
|
Droite de Van Aubel
|
|
Géométrie du triangle - Points caractéristiques
|
Point de Lemoine
Symédianes et point de Lemoine
Triangle tangentiel
Point de Gergonne
Point de Nagel
Point de Bevan
Point de Fermat
Triangle intérieur de Napoléon
MittenPunkt
|
|
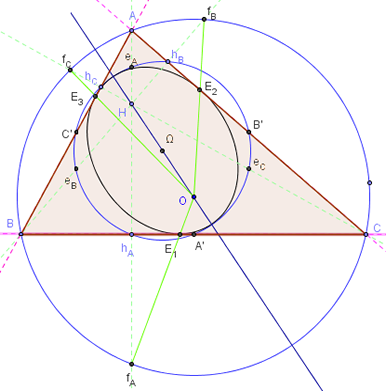
Droite et cercle d'Euler
|
Cercle d'Euler
Cercle d'Euler circonscrit au triangle orthique
Hexagramme inscrit dans le cercle d'Euler
|
|
Géométrie du triangle - Cercles remarquables
Théorème et points de Feuerbach
|
Théorème de Feuerbach
Point de Feuerbach - Alignement de 4 points
Point de Feuerbach - Alignement avec les centres
Droites concourantes au point de Feuerbach
Point de Feuerbach et bissectrices
Trois cercles inscrits dans un triangle rectangle
|
|
|
Triangle isocèle |
|
Relations métriques dans le triangle
|
Formule des aires
Cercle inscrit dans un triangle et distances
|
|
Triangles rectangles
|
Construction du triangle égyptien avec Thalès
Cercle inscrit dans un triangle rectangle
Trois cercles inscrits du triangle rectangle
Rayons de cercles inscrits du triangle rectangle
Cercles du triangle rectangle tangents au circonscrit
Théorème japonais de Carnot dans le triangle rectangle
|
|
Triangle équilatéral
|
Triangle équilatéral
Deux triangles équilatéraux symétriques
Quadrature du triangle équilatéral
|
|
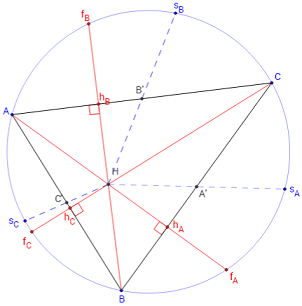
Triangle orthique
|
Triangle orthique
Trois cercles pour les bissectrices du triangle orthique
Les hauteurs sont les bissectrices du triangle orthique
Parallèle à un côté du triangle orthique
Axe orthique
Médiatrice d'un côté du triangle orthique
Cercle d'Euler circonscrit au triangle orthique
Perspective des triangles médian et tangentiel
|
|
Triangles autour d'un triangle BOA
|
Deux triangles à l'extérieur d'un triangle
Médiane de l'un, hauteur de l'autre
Quatre triangles équilatéraux
|
|
Carrés autour d'un triangle BOA
|
Hauteur de l'un, médiane de l'autre
Deux carrés autour d'un triangle - hauteurs - médianes
Deux triangles rectangles, parallélogrammes, hauteurs, médianes
Figure de Vecten - Deux segments orthogonaux
Figure de Vecten - Démonstration de l'orthogonalité
Point de Vecten
Point intérieur de Vecten
Carrés de Malfatti
|
|
Triangle inscrit dans un triangle
|
Aire d'un triangle inscrit égale aux 5/16 de l'aire du triangle circonscrit
Aire d'un triangle inscrit égale aux 7/16 de l'aire du triangle circonscrit
Transformer un quadrilatère en triangle en 3 étapes
Transformer un quadrilatère en triangle (version avec un seul quadrilatère)
Transformer un quadrilatère en triangle dans le géoplan 5 × 5
|
|
La planche à clous comme géoplan
|
aire d'un triangle du géoplan 5 sur 5
Triangle du géoplan 3 × 3
Carré dans le géoplan 4 sur 4
Quadrilatère orthodiagonal du géoplan 5 sur 5
|
|
Les quadrilatères au collège
|
Médianes et centre de gravité d'un quadrilatère |
|
Le carré au collège
|
Moulin à vent du géoplan 4 × 4
Moulin à vent d'Euclide dans un quadrillage
Moulin à vent du géoplan 6 sur 6
|
|
Le parallélogramme au collège
|
Théorème de Varignon
|
|
Empilements dans le plan
|
Deux carrés dans un cercle
Trois carrés dans un cercle
Trois carrés autour d'un triangle équilatéral
Cinq carrés dans un cercle
Huit carrés dans un cercle
|
|
Homothétie
|
Carré inscrit dans un triangle
|
|
Similitudes
|
Alignement dans une similitude
|
|
Inversion de cercles
|
Inverseur de Peaucellier
Inverseur de Peaucellier 2
Inverseur de Peaucellier - image d'une droite
Inverse d'un cercle
Inversions échangeant deux cercles sécants
Inversions échangeant deux cercles extérieurs
Tangentes aux points antihomologues d'une inversion
Deux couples de points antihomologues d'une inversion
Inversion entre le cercle circonscrit et le cercle d'Euler
Inverse d'une droite qui rencontre le cercle d'inversion
Inversion d'une droite extérieure au cercle d'inversion
|
|
 Le plan projectif
|
Trapèze complet
Quadrilatère complet
Divisions harmoniques du quadrilatère complet
Droite de Newton d'un triangle
Point de Miquel
Cercles de Miquel
|
|
Puissance d'un point par rapport à un cercle
|
Puissance d'un point par rapport à un cercle
Médiane et puissance d'un point
|
|
Aire d'un triangle à l'intérieur d'un parallélogramme
|
Triangle construit dans un parallélogramme
Aire d'un triangle dans un parallélogramme
Théorème de Pick
|
|
Calculs d'aires par découpage
|
Duplication du rectangle
Duplication du triangle
|
|
Rotation au collège
|
Orthocentre d'un triangle inscrit dans un carré
Aire d'un quadrilatère intersection de deux carrés
|
|
Aires du parallélogramme et du trapèze
|
Deux triangles dans un trapèze
|
|
Optimisation en classe de troisième
|
Aire maximale d'un rectangle de diagonale constante
Aire d'un rectangle de diagonale constante
Distance minimale dans un triangle rectangle
Statue de La Liberté de New York
|
|
Angles inscrits au collège
|
Angle de la corde et d'une tangente
|
|
Optimisation en classe de seconde
|
Optimisation des aires d'un carré et d'un triangle
Aire délimitée par un périmètre de baignade
Aire minimale de deux carrés dans un carré
Aire minimale d'un triangle dans un rectangle
|
|
Le rectangle au collège
|
Diagonale mobile d'un rectangle
|
|
Rectangle variable inscrit dans un triangle rectangle
|
Carré inscrit dans un triangle rectangle
|
|
Exercices de géométrie au collège
|
Triangle de l'écolier
Triangle rectangle et bissectrice
Projections du centre du cercle inscrit
Bissectrice et triangle isocèle
Carré et triangle équilatéral
Carré, cercles et tangente
Triangles et alignement
Bissectrices d'un parallélogramme
Triangle et trapèze
|
|
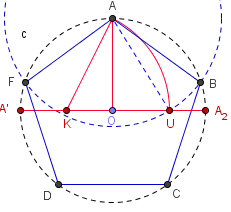
Construire un pentagone régulier
|
Pentagone régulier
Construction de Ptolémée du pentagone (sommer A à droite)
Construction de Ptolémée du pentagone (sommer A en haut)
Construction d'architecte du pentagone
Pentagramme
|
|
Polygone régulier
|
Hexagone
Octogone
Octogone dans un carré
Octogone et triangles équilatéraux
Octogone étoilé
Dodécagone et triangles équilatéraux
|
|
Droites perpendiculaires dans un carré – utiliser un orthocentre
|
Droites perpendiculaires autour d'un triangle rectangle
Droites perpendiculaires dans un carré
|
|
Le cercle au collège
|
Cercle tangent à une droite et deux points
Centre d'un cercle
|
|
Montrer un alignement
|
Carré et deux triangles équilatéraux
Carré et triangles équilatéraux
Alignement sur la diagonale d'un carré
Alignement avec le sommet d'un triangle
Alignement avec le sommet d'un triangle - Démonstration
|
|
Constructions par pliage
|
Partage en cinq de la diagonale d'un rectangle
Partage de la diagonale d'un rectangle aux 3/10
Partage aux trois onzième du rectangle
Pliage d'un rectangle selon une diagonale
|
|
Nombre d'or
|
Construction de rectangles d'or
Diagonales des rectangles d'or
Tracé régulateur - Présentation de la Vierge
Cercle inscrit dans le triangle égyptien
|
|
Constructions géométriques au collège
|
Quadrature du rectangle
|
|
Construction avec contraintes
|
Fleur de 6 losanges
Trois cercles égaux tangents à l'intérieur d'un triangle |
|
Échelle appuyée contre un mur
|
Échelle contre un mur
|
|
Deux triangles inscrits dans deux cercles de rayons 1
|
Deux triangles inscrits dans deux cercles
|
|
Machine à marcher
|
Machine à marcher de Tchebychev
|
|
Trisection de l'angle
|
Trisection avec une équerre en L
Trisection avec une équerre de Grisel
|
|
Paraboles
|
Parabole définie par ses coefficients
Parabole et homothétie
Image d'une parabole par homothétie
Hyperboles homothétiques
|
|
Newton (1643-1727)
|
Ellipse de Newton tangente à 5 droites
|
|
Descartes et le Problème de Pappus
|
Problème de Pappus
Cercle solution du problème de Pappus
Parabole du problème de Pappus
Conique de Pappus passant par un point donné
|
|
Calcul de Mons. des Cartes
|
Triangle avec un angle, un côté et la somme des autres
Deux triangles rectangles formant un papillon
Lieu d'Apollonuis
Un triangle avec un angle, un côté…
|
|
|
Sur tablette numérique ou smartphone, bascule automatique vers la version mobile
…
