L'espace en sixième - Parallélépipède

Descartes et les Mathématiques L'espace en sixième avec GeoGebra Parallélépipède rectangle : patrons avec GeoGebra 3D.
Sommaire 1. Cube : perspective cavalière 2. Parallélépipède rectangle 3. Patron d'un parallélépipède rectangle	Technique GeoGebra : patron d'un polyèdre Sur tablette numérique ou smartphone, bascule automatique vers la version mobile
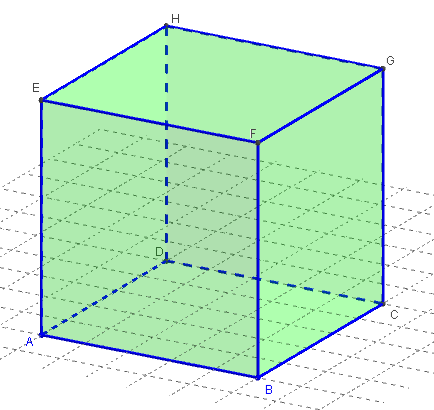
1. Le cube : perspective cavalière Le cube dans GeoGebra est défini par deux points et le plan (xOy) ou une direction; Il fallait y penser ! Il est possible de faire tourner la figure. a³ est le volume du cube de côté a Volume(ABCDEFGH) = Aire de la base × hauteur = Aire(ABCD) × AE = a² × a = a³. Figures 3D dans GeoGebraTube : cube, cube sur grille, cube en fil de fer Opacité Dans les propriétés du cube, choisir l'onglet couleur et régler l'opacité à 25, - choisir 0 pour une figure en fil de fer, - 100 pour une figure opaque.
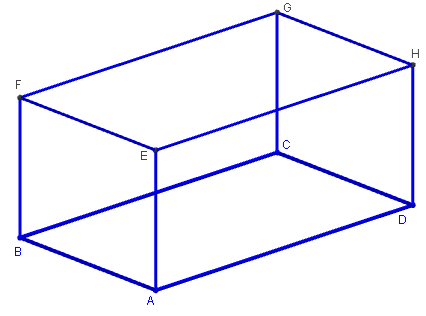
2. Parallélépipède rectangle Définition du parallélépipède Parallélépipède : polyèdre à six faces qui sont toutes des parallélogrammes. Les faces opposées sont égales et parallèles. Parallélépipède rectangle : polyèdre à six faces qui sont toutes des rectangles. À l'école, le terme parallélépipède rectangle n'est pas exigible au cycle 2, on lui préférera celui de pavé droit. Volume du parallélépipède rectangle AB = a, AD = b et AE = c. Volume(ABCDEFGH) = Aire de la base × hauteur = Aire(ABCD) × AE = AB × AD × AE = a × b × c. Commandes GeoGebra La figure en fil de fer est obtenue en choisissant 0 comme coefficient d'opacité. Modifier les mesures des côtés. Décocher la case pour effacer les diagonales. 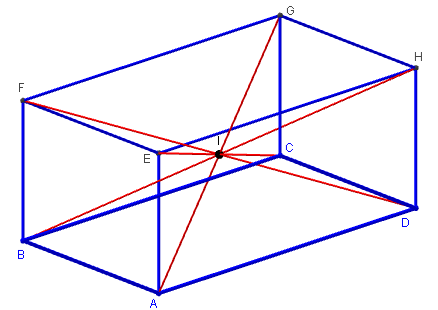Figure 3D dans GeoGebraTube : pavé droit	Les diagonales sont concourantes en leur milieu Par exemple, les diagonales [AG] et [EC] sont les diagonales du rectangle ACGE. Elles se coupent en leur milieu I. Longueur d'une diagonale du parallélépipède rectangle Classe de quatrième Pour calculer la longueur AG; il est possible d'utiliser le théorème de Pythagore dans deux plans différents : dans le triangle rectangle ABC, AC² = a² + b², dans le triangle rectangle ACG, AG² = AC² + CG² = (a² + b²) + c². La longueur de la diagonale est donnée par AG² = a² + b² + c². Figure 3D dans GeoGebraTube : diagonales du parallélépipède rectangle Cas particulier : longueur d'une diagonale du carré de côté a dans le triangle rectangle isocèle ABC, AC² = a² + a² = 2a², dans le triangle rectangle ACG, AD² = AC² + CG² = (2a²) + a² = 3a². La longueur de la diagonale du cube est AG = a
3. Patron d'un parallélépipède rectangle



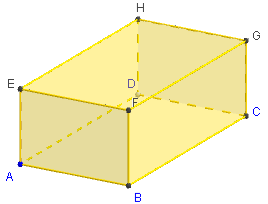
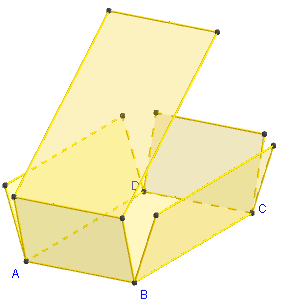
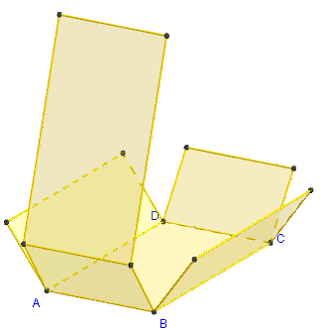
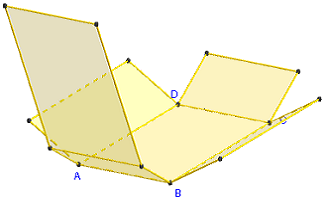
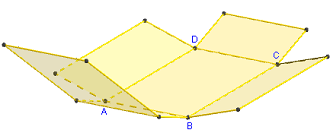
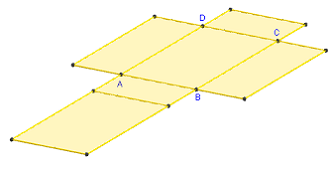
Commandes GeoGebra Le patron est pilotable en faisant varier le coefficient d'ouverture m de 0 vers 1. Figure 3D dans GeoGebraTube : patron du pavé droit
Technique GeoGebra : patron d'un polyèdre On obtient, parmi tous les patrons possibles, un patron choisi par le logiciel à partir de la face principale ayant servi à sa construction.. Les autres faces s'articulent autour de cette face. Abus de langage de Google Patron d'un rectangle : patron d'un parallélépipède rectangle de base rectangulaire, Patron d'un triangle : patron d'un prisme de base triangulaire.

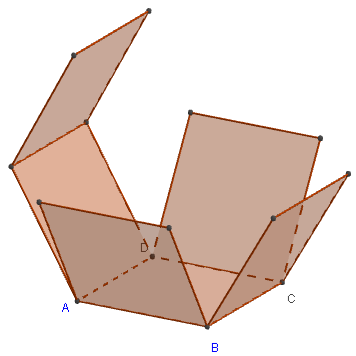
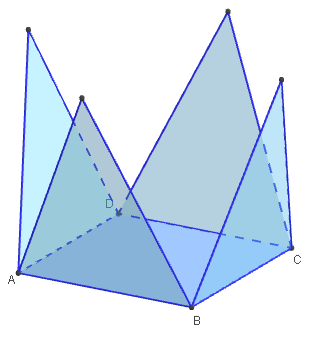
Classe de sixième – Patron de cube Figure 3D dans GeoGebraTube : patron du cube	Classe de quatrième - Patron de pyramide Figures 3D dans GeoGebraTube : pyramide de base carrée, patron de pyramide de base carrée
Le coefficient d'ouverture du patron est une variable réelle m, comprise entre 0 et 1 ; si elle est égale à 1 le patron est plan, si elle est égale à 0 le patron coïncide avec le polyèdre.
Table des matières Figures dynamiques Les figures de cette page avec GéoSpace …Avec GeoGebra 3D dans d'autres pages du site GeoGebra 3D en 5^e : prisme GeoGebra 3D en 4^e : Pyramides GeoGebra 3D en 3^e : Sections planes Mode d'emploi GeoGebra 3D
Page n^o 84, réalisée le 27/6/2005 adaptée à GeoGebra 3D le 10/10/2014