Descartes et les Mathématiques
L'espace en quatrième avec GeoGebra 3D
Pyramide : volume, patron - partition d'un cube en trois ou six pyramides - Cône de révolution.
La géométrie dans l'espace en quatrième
Pyramide : le cours
1. Coin de cube
4. Pyramide équilatérale de base carrée
5. Patrons de pyramide et de tétraèdre
6. Cône de révolution
Sur tablette numérique ou smartphone, bascule automatique vers la version mobile
La pyramide dans d'autres pages du site
Sections planes de pyramide (troisième)
Intersection de plans dans une pyramide (seconde)
…Avec GeoGebra 3D
Mode d'emploi GeoGebra 3D
Sections planes en 3e cube, pyramide
Pyramide : le cours
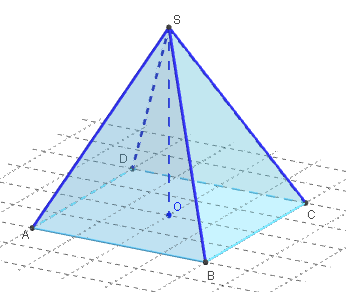
Une pyramide est un solide composé :
• d'une base polygonale,
• de faces latérales triangulaires, ayant un sommet commun, le sommet de la pyramide.
Pyramide régulière
Définition : la pyramide est régulière si la base est un polygone régulier et si la hauteur, perpendiculaire abaissée du sommet sur la base, a son pied au centre du polygone de base.
Pyramide au collège
Au collège, les pyramides étudiées auront une base rectangulaire, souvent carrée, ou bien une base triangulaire ; dans ce dernier cas, le solide est nommé tétraèdre.
Cas particuliers
Toutes les arêtes sont de même longueur :
• base triangulaire : le tétraèdre régulier,
• base carrée : la pyramide équilatérale où les faces latérales sont des triangles équilatéraux;
le triangle ACS dans le plan diagonal est rectangle isocèle.
Autre cas particulier de pyramide régulière de base carrée :
• le triangle ACS du plan diagonal est équilatéral.
Figure 3D dans GeoGebraTube : pyramide de base carrée
Voir : tronc de pyramide
Formule du volume d'une pyramide
Le volume V d'une pyramide (d'un tétraèdre ou d'un cône de révolution) est donné par la formule :
V = 
× aire de la base × hauteur = × Sbase × hauteur,
où Sbase est l'aire de la base et hauteur = OS (figure ci-dessus).
Démocrite (460-370 avant J.-C.) fut le premier à formuler l'énoncé et Eudoxe (IVe siècle) le premier à en trouver la démonstration.
Volume d'une pyramide à base carrée
Si la base carrée ABCD a pour côté a, Sbase = a2.
Le volume est alors : V = × a2 × hauteur = × a2 × OS.
1. Coin de cube
On appelle « coin de cube » le tétraèdre trirectangle BEGF formé par trois arêtes d'un cube concourantes en un sommet F, et des diagonales des faces du cube qui joignent les autres extrémités de ces arêtes.
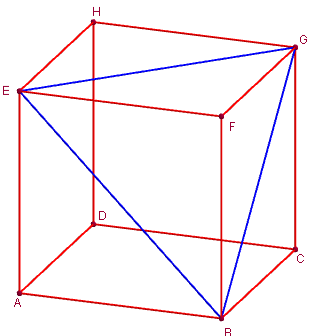
« Figure fil de fer ».
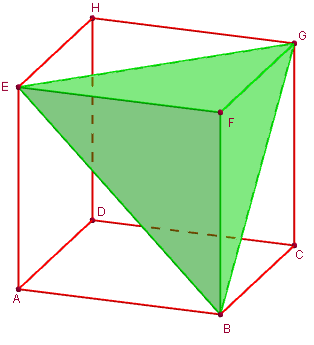
En vert : « coin de cube ».
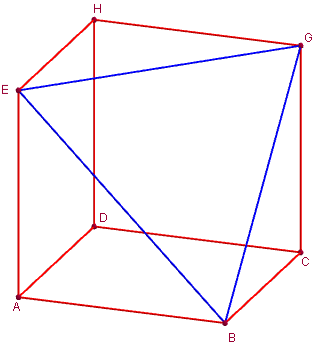
« Cube fortement tronqué ».
En classe de quatrième, savoir visualiser le « coin de cube » à partir de la « figure fil de fer » à gauche et se représenter ci-contre le « cube fortement tronqué », cube auquel on a enlevé un coin de cube.
Figures 3D dans GeoGebraTube : coin de cube
– Coin de cube dans un cube en fil de fer
- on y trouve les trois variantes : triangle équilatéral formé par trois diagonales de faces du cube - cube moins coin de cube - cube fortement tronqué
Voir aussi : « cube tronqué » aux huit sommets.
2. Trois pyramides inscrites dans un cube
Visualiser la partition d'un cube en 3 pyramides à bases carrées, au total ayant donc le même volume.
Pour cela, on va partir du cube initial ABCDEFGH, définir les trois pyramides de même sommet E et de bases respectives les trois faces ABCD ; BCGF et HDCG du cube.
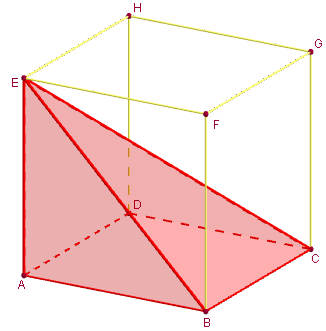
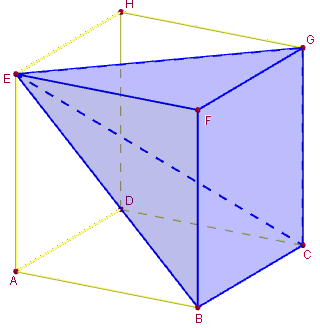
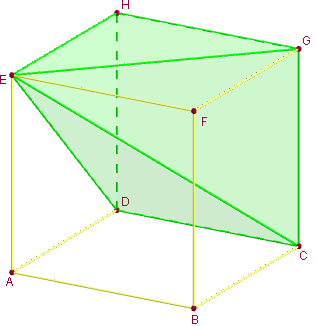
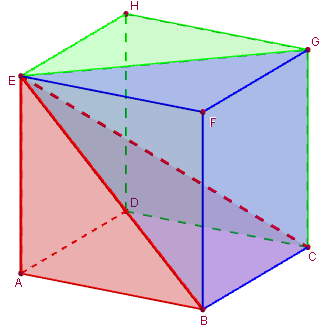
On vérifie que le volume de chaque pyramide est bien V = × a3 = × a2 × a = × Sbase × hauteur.
Figures 3D dans GeoGebraTube : trois pyramides inscrites dans un cube
3. Six pyramides dans un cube
Partition du cube en 6 pyramides régulières de bases carrées les faces du cube, de sommet le centre du cube.
La réunion des six pyramides a le même volume que le cube.
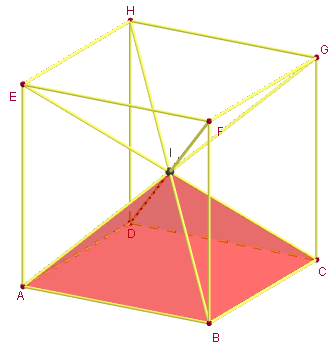
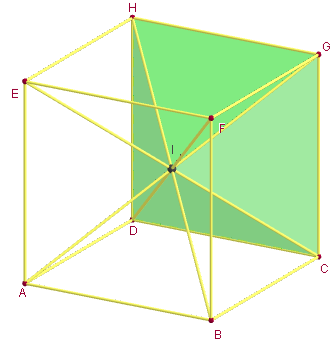
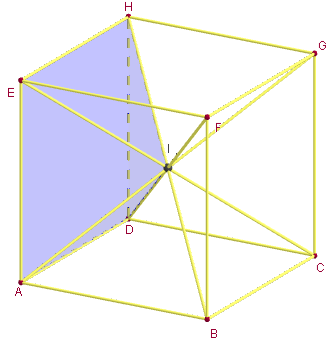
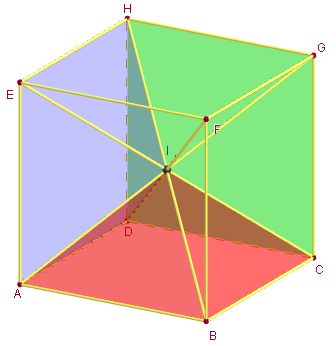
Par symétrie on peut compléter ces trois pyramides pour obtenir une partition du cube en six pyramides de même volume.
On retrouve encore le volume de la pyramide V = 
× a3 = × a2 × 
a = × Sbase × hauteur.
Figures 3D dans GeoGebraTube : six pyramides inscrites dans un cube, diagonales d'un cube en fil de fer
4. Pyramide régulière de base carrée
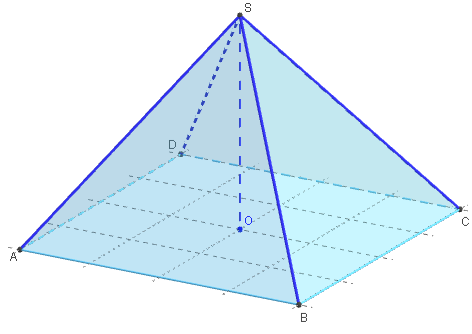
Comment dessiner une pyramide 3D ?
4.1. Dessiner une pyramide équilatérale de base carrée.
SABCD est une pyramide régulière de base carrée ABCD.
Elle est équilatérale si les quatre autres faces sont des triangles équilatéraux.
Quel est l'angle des arêtes (SA) et (SC) ?
Construction de la pyramide équilatérale
Construire un carré de côté a. Ses diagonales [AC] et [BD] se coupent en O. La hauteur (d) est la droite issue de H, perpendiculaire au plan ABC.
S est un des points d'intersection de la hauteur (d) et de la sphère de centre A et de rayon a.
AOS est un triangle rectangle isocèle d'hypoténuse a : la hauteur SO est alors égale à a
.
Plan diagonal
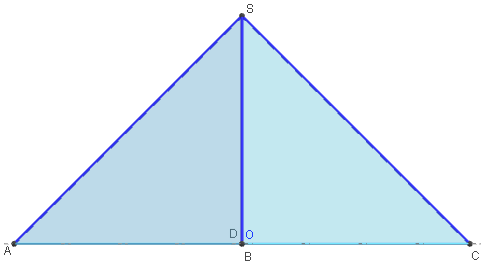
Une vue de face du triangle ACS dans le plan diagonal permet de conjecturer que l'angle ASC est droit.
En effet, si a est la longueur d'une des arêtes de la pyramide, on remarque que ABC est un triangle rectangle isocèle de petits côtés a et d'hypoténuse AC.
Le triangle ASB a deux côtés de longueur a et un troisième côté AC.
Il est isométrique à ABC : ASB est rectangle en S.
Figure 3D dans GeoGebraTube : pyramide de base carrée
cocher la case pyramide équilatérale
Deux fenêtres pour cette pyramide équilatérale
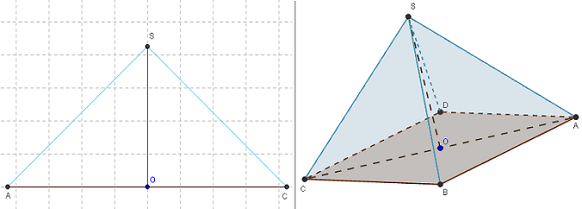
Cadre de gauche : plan (ACS) dans la fenêtre graphique (xOy) ; diagonale [AC] de la base sur (Ox), S sur (Oy) axe vertical.
Triangle ACS, du plan diagonal, rectangle isocèle, en vraie grandeur, dans la fenêtre graphique.
4.2. Triangle ACS, du plan diagonal, équilatéral
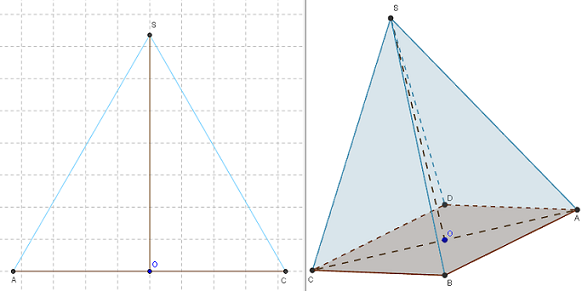
Figure 3D dans GeoGebraTube : pyramide de base carrée - plan diagonal
Selon le triangle ACS du plan diagonal, cocher les cases :
• ou triangle équilatéral,
• Cocher la case triangle rectangle isocèle (ci-dessous).
5. Technique GeoGebra 3D :
Patron d'un polyèdre
On obtient, parmi tous les patrons possibles, un patron choisi par le logiciel à partir de la face principale ayant servi à sa construction.
Les autres faces s'articulent autour de cette face.
5.1. Patron d'une pyramide de base c arrée
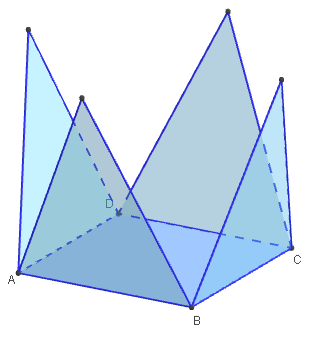
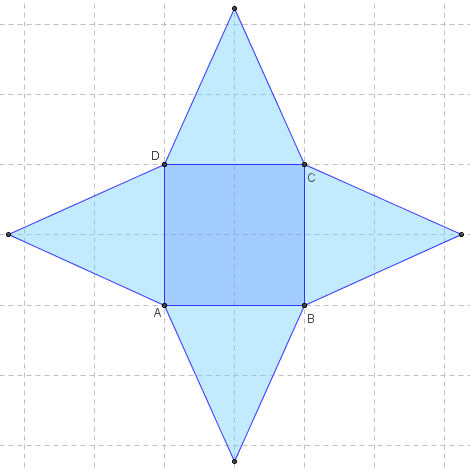
Comment dessiner une pyramide à base carreée
5.2. Patron d'un tétraèdre réguler
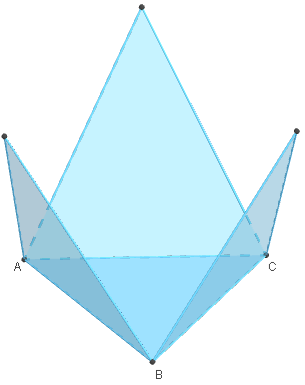
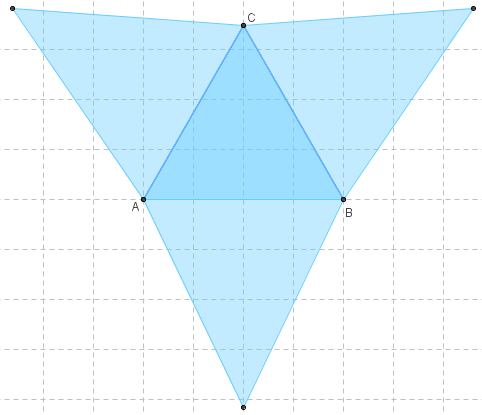
Patron d'une pyramide de base triangulaire
Figure 3D dans GeoGebraTube : patron de pyramide de base carrée
Figures 3D dans GeoGebraTube : tétraèdre de base un triangle équilatéral, patron d'un tétraèdre
Le coefficient d'ouverture du patron est une variable réelle m, comprise entre 0 et 1 ; si elle est égale à 1 le patron est plan, si elle est égale à 0 le patron coïncide avec le polyèdre.
6. Cône de révolution
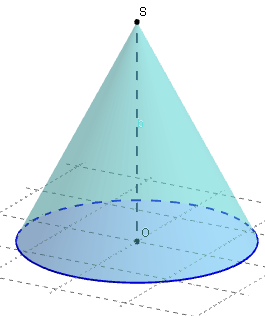
Pour ce cône, la base est un cercle de centres O et de rayon r.
L'axe (OS) du cône est perpendiculaire au plan du cercle de base.
Volume du cône
Pour le cercle de rayon r, l'aire de la base est πr2 ;
la longueur h de la hauteur [OS] est égale à la distance du sommet à la base.
Volume = V = × aire de la base × hauteur = × Abase × h.
Volume = B × h = πr2 × SO = πr2h.
Aire latérale du cône
L'apothème, distance du sommet au cercle, est rac(r2 + h2).
L'aire latérale d'un cône de révolution sans la base : 2πr rac(r2 + h2).
Figure 3D dans GeoGebraTube : cône de révolution
Table des matières
Les figures de cette page avec GéoSpace
Téléchargement
Télécharger geospace_quatrieme.doc :
Google considère l'URL de ce document au format « .doc »comme une erreur de type "soft 404".
Télécharger geospace_quatrieme.pdf : ce document au format « .pdf »
Page no 85, réalisée le 5/9/2005
adaptée à GeoGebra 3D le 13/10/2014