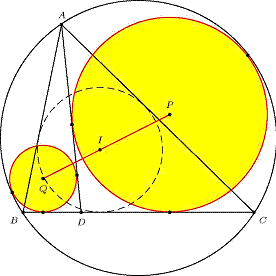
Figure 1
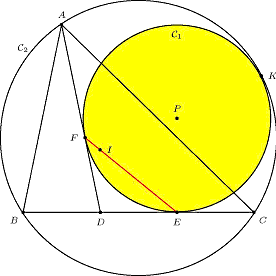
Figure 2
Ayant travaillé en 2003 sur la configuration de Van Aubel ; j'ai découvert le théorème de Thébault dans le dictionnaire des mathématiques et j'ai créé, en mai 2008, une page WikiPédia qui a reçu des enrichissement conséquents des utilisateurs Tcharvin et HB.
WikiPédia : théorème de Thébault
Ayant quelques soucis avec l'anglais (je ne sais pas y distinguer cause et conséquence), j'ai traduis la page ci-dessous pour éclaircir mes idées sur les démonstrations.
Je ne sais si cela est publiable et j'attend la réponse de l'auteur pour savoir si je peux le faire et où.
J'ai du mal avec la construction qui n'est pas explicitée. Je me suis contenté de Viète, merci à HB qui m'a indiqué la méthode des bissectrices.
Voir en annexe à la fin de l'article.
Le nom de théorème de Thébault ne correspond pas à un théorème précis, mais plutôt à une série de problèmes posés par le mathématicien français Victor Thébault (1882 - 1960).
Construction de quatre carrés à l'extérieur d'un parallélogramme ABCD.
Deux triangles équilatéraux autour d'un carré.
Le problème de Thébault no3, aussi connu sous le nom de Théorème de Sawayama-Thébault, est un théorème de géométrie euclidienne portant sur l'alignement de trois points dans une construction.
La première démonstration connue a été réalisée en 1973 par le mathématicien néerlandais H. Streefkerk.
Jean-Louis Ayme a publié, en 2003, une solution synthétique de ce problème. Il a également effectué des travaux historiques sur celui-ci et a découvert que ce théorème avait été démontré en 1905 par Y. Sawayama, instructeur à l'école militaire de Tokyo.
|
Sawayama and Thebault’s theorem Forum Geom. 3, 225-229, 2003. Abstract. We present a purely synthetic proof of Thebault’s theorem, known earlier to Y. Sawayama. 1. Introduction |
Théorème de Thébault − Sawayama Nous présentons une preuve purement synthétique de Théorème de Thébault, connu plus tôt par Y. Sawayama. 1. Introduction En 1938, dans “Problems and Solutions” section du Amer. Math. Monthly [24], le célèbre mathématicien français Victor Thébault (1882-1960) a proposé un problème sur trois cercles de centres colinéaires (voir figure 1) à quoi il ajoute un rapport et corrige une relation qui finalement s'est avérée être fausse. |
 Figure 1 |
 Figure 2 |
|
Proof. Let M, N be the points of intersection of KE, KF with C2, and J the point of intersection of AM and EF (see Figure 3). KE is the internal bisector of ∠BKC [8, Theoreme 119]. The point M being the midpoint of the arc BC which does not contain K, AM is the A-internal bisector of ABC and passes through I. The circles C1 and C2 being tangent at K, EF and MN are parallel. |
Preuve. Soit M, N les points d'intersection de C2 avec KE et KF, et J le point d'intersection de AM et EF (voir Figure 3). KE est la bissectrice intérieure de BKC [8, Théorème 119]. Le point M est le milieu de l'arc BC qui ne contient pas de K, AM est la bissectrice intérieure de l'angle A de ABC et passe par I. Les cercles C1 et C2 sont tangents en K, EF et MN sont parallèles. (Note du traducteur : MN est l'image de EF dans l'homothétie de centre K qui transforme C1 en C2.) |
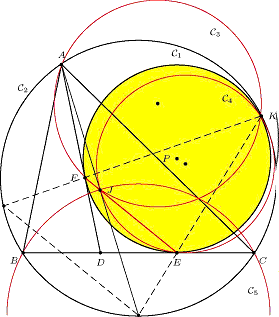 Les noms des points M et N ont disparu dans la copie de l'image ? |
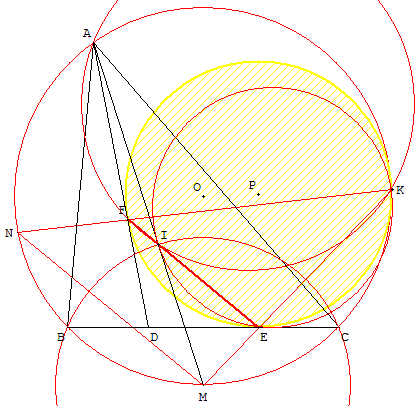 |
Figure 3
Question : E et F sont situés sur la parallèle passant par I à la bissectrice de ADB. Ceci ne peut être utilisé que lorsque le lemme a été prouvé. Alors comment caractériser E et F ? ou K ? ou les cercles C3 et C4 ? Comment utiliser C5 ?
|
The circle C2, the basic points A and K, the lines MAJ and NKF, the parallels MN and JF, lead to a converse of Reim’s theorem ([8, Theoreme 124]). Therefore, the points A, K, F and J are concyclic. This can also be seen directly from the fact that angles FJA and FKA are congruent. From ∠BKE = ∠MAC = ∠MBE, we see that he circumcircle of BKE is tangent to BM at B. So circle C5 is orthogonal to this circumcircle and consequently also to C1 as M lies on their radical axis. Therefore, MB = MJ, and J = I. Conclusion : the chord of contact EF passes through the incenter I. Remark. When D is at B, this is the theorem of Nixon [16]. 3. Sawayama-Thebault theorem Theorem 2. Through the vertex A of a triangle ABC, a straight line AD is drawn, cutting the side BC at D. I is the center of the incircle of triangle ABC. Let P be the center of the circle which touches DC, DA at E, F, and the circumcircle of ABC, and let Q be the center of a further circle which touches DB, DA in G, H and the circumcircle of ABC. Then P, I and Q are collinear. |
Le cercle C2, les points de base A et K, les lignes MAJ et NKF, les parallèles MN et JF, conduisent à une application de Théorème de Reim ([8, théorème 124]). Par conséquent, les points A, K, F et J sont cocycliques. Cela peut aussi être vu directement du fait que les angles FJA et FKA sont égaux. Des angles BKE = MAC = MBE, nous voyons que le cercle circonscrit de BKE est tangent à BM en B. Donc, le cercle C5 est orthogonal à ce cercle circonscrit et, par conséquent, également à C1, M se trouvant sur leur axe radical. Par conséquent, MB = MJ, et J = I. Conclusion : la corde de contact EF passe par le centre I du cercle inscrit. Remarque. Lorsque D est en B, c'est le théorème de Nixon [16]. 3. Théorème de Sawayama-Thébault Théorème 2. Par le sommet A du triangle ABC, un segment AD est mené, qui coupe le côté BC en D. I est le centre du cercle inscrit dans le triangle ABC. Soit P le centre du cercle tangent à DC, DA en E, F et le cercle circonscrit de ABC, et soit Q le centre d'un nouveau cercle qui tangent à PB, DA aux points G, H et tangent au cercle circonscrit de ABC. Alors, P, I et Q sont colinéaires. |
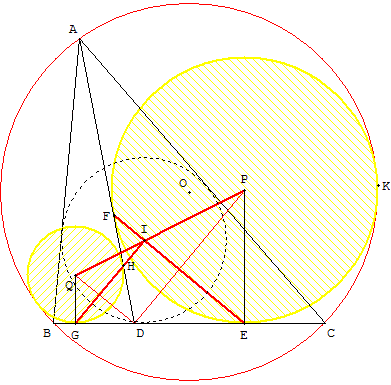
Figure 4
|
Proof. According to the hypothesis, QG ⊥ BC, BC ⊥ PE ; so QG//PE. By Lemma 1, GH and EF pass through I. Triangles DHG and QGH being isosceles in D and Q respectively, DQ is
Mutatis mutandis, DP is
As the bisectors of two adjacent and supplementary angles are perpendicular, Conclusion : using the converse of Pappus’s theorem ([17, Proposition 139] and [3, p.67]), applied to the hexagon PEIGQDP, the points P, I and Q are collinear. |
La preuve. Selon les hypothèses, QG ⊥ BC, BC ⊥ PE de sorte QG // PE. Par le lemme 1, GH et EF passent par I. Les triangles DHG et QGH sont isocèles respectivement en D et Q, DQ est
Mutatis mutandis, DP est
Comme les bissectrices de deux angles adjacents sont perpendiculaires, Conclusion : en utilisant la réciproque du Théorème de Pappus ([17, proposition 139] et [3, p. 67]), appliquée à l'hexagone PEIGQDP, les points P, I et Q sont colinéaires. |
References
[1] N. Altshiller-Court, College Geometry, Barnes & Noble, 205.
[2] E. Catalan, Théorèmes et problèmes de géométrie élémentaire, 1879.
[3] H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, Math. Assoc. America, 1967.
[4] Archiv der Mathematik und Physik (1842) 328.
[5] B. C. Dijkstra-Kluyver, Twee oude vraagstukken in eén klap opgelost, Nieuw Tijdschrift voor Wiskunde, 61 (1973-74) 134-135.
[6] B. C. Dijkstra-Kluyver and H. Streefkerk, Nogmaals het vraagstuk van Thebault, Nieuw Tijdschrift voor Wiskunde, 61 (1973-74) 172-173.
[7] B. J. English, Solution of Problem 3887, Amer Math. Monthly, 110 (2003) 156-158.
[8] F. G.-M., Exercices de géométrie, sixième édition, 1920, J. Gabay reprint.
[9] H. G. Forder, Geometry, Hutchinson, 1960.
[10] L. Gaultier (de Tours), Les contacts des cercles, Journal de l'Ecole Polytechnique, Cahier 16 (1813) 124-214.
[11] S. Gueron, Two Applications of the Generalized Ptolemy Theorem, Amer Math. Monthly, 109 (2002) 362-370.
[12] R. A. Johnson, Advanced Euclidean Geometry, Dover, 1965.
[13] Leybourn's Mathematical Repository (Nouvelle série) 6 tome I, 209.
[14] A. Miquel, Théorèmes de géométrie, Journal de mathématiques pures et appliquées de Liouville, 3 (1838) 485-487.
[15] J. Neuberg, Nouvelle correspondance mathématique, 1 (1874) 96.
[16] R. C. J. Nixon, Question 10693, Reprints of Educational Times, London (1863-1918) 55 (1891) 107.
[17] Pappus, La collection mathématique, 2 volumes, French translation by Paul Ver Eecker, Paris, Desclée de Brouver, 1933.
[18] Y. Sawayama, A new geometrical proposition, Amer. Math. Monthly, 12 (1905) 222–224.
[19] R. Shail., A proof of Thébault’s Theorem, Amer. Math. Monthly, 108 (2001) 319–325.
[20] S. Shirali, On the generalized Ptolemy theorem, Crux Math., 22 (1996) 48–53.
[21] R. Stark, Eine weitere Lo¨sung der Thébault’schen Aufgabe, Elem. Math., 44 (1989) 130–133.
[22] H. Streefkerk, Waarom eenvoudig als het ook ingewikkeld kan?, Nieuw Tijdschrift voor Wiskunde, 60 (1972-73) 240–253.
[23] K. B. Taylor, Solution of Problem 3887, Amer. Math. Monthly, 90 (1983) 482–487.
[24] V. Thébault, Problem 3887, Three circles with collinear centers, Amer. Math. Monthly, 45 (1938) 482–483.
[25] G. Turnwald, U¨ ber eine Vermutung von Thébault, Elem. Math., 41 (1986) 11–13.
[26] G. R. Veldkamp, Een vraagstuk van Thébault uit 1938, Nieuw Tijdschrift voor Wiskunde, 61 (1973-74) 86–89.
[27] G. R. Veldkamp, Solution to Problem 1260, Crux Math., 15 (1989) 51–53.
Construction des bissectrices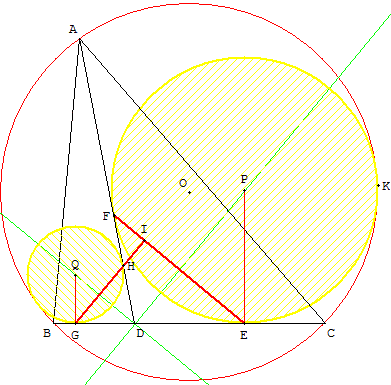 On trace les bissectrices issues de D et leurs parallèles issues du centre du cercle inscrit. Elles rencontrent les segments [DA], [DC], [DB] aux points de contact des cercles tangents. Il suffit de mener les perpendiculaires à [DC] et [DB] par ces points de contact, elle rencontre les bissectrices au centre des cercles tangents. On a le centre du cercle et un point de contact, cela suffit pour tracer les cercles. GeoGebra fournit le point de contact K, sinon on peut toujours se servir du fait que les centres de deux cercles sont alignés avec le point de contact. HB (d) 7 juillet 2008 à 15:21 |
Construction de Viète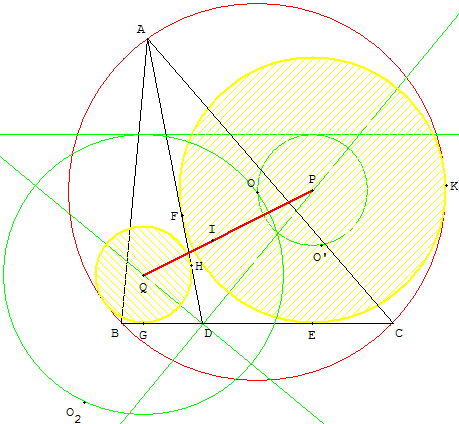 O’ et O2 sont les symétriques de O par rapport aux bissectrices issues de D. Tracer les cercles passant par O et O’ ou O et O2 tangent à la parallèle à (BC) située à une distance de (BC) égale au rayon du cercle circonscrit. Tracer leurs centres P et Q. Tracer les cercles de centre P et Q tangents à (BC).
|
|
Jean-Louis Ayme Accueil Descartes et les Mathématiques | |||
|
|
Traduction PDebart. |