Descartes et les Mathématiques

La Géométrie dans l'espace en troisième avec GéoSpace

Problèmes de sections planes de solides - Sphère.

GéoSpace en 3^e

1. Sections planes d'un cube
2. Sections et tronc de pyramide
3. Section et t ronc de tétraèdre - Solide composite
            Lanterne
            bac STI (AA) 1999
4. Sections planes de solides de révolution
5. Une fuite de robinet

Sur tablette numérique ou smartphone, on bascule automatiquement vers la version GeoGebra 3D

Sections planes du cube

Cube en 2^nde
Intersection d'un plan et d'un cube

Pyramide : le cours

Partition d'un cube en trois ou six pyramides
Pyramide octogonale

Sections planes de pyramide
Parallélépipède dans une pyramide au bac

Travaux Pratiques 1

A. Sections planes d'un cube

« L'utilisation de l'informatique donne une vision dynamique de la figure. GéoSpace permet de faire tourner le cube et de mettre en évidence la section cherchée. La possibilité de placer un plan isolé de face permet de voir les sections planes en “vraie grandeur”.
Les commandes “dessin en bloc” facilitent la présentation par le professeur avec un rétroprojecteur. »

1.1. Rectangle comme section du cube

Section du cube par un plan contenant une arête

Charger la figure GéoSpace de base : cube.g3w.

Créer le point variable I, sur le segment (arête du cube) [BF].
Trouver le point J intersection du plan (ADI) avec la droite (CG).
Tracer les segments [AI], [IJ] et [JD] en tapant les noms des segments dans le menu : ligne > segment.

Déplacer le point I.

Quelle est la nature de la section du cube par le plan (ADI) ?

Figure 3D dans GeoGebraTube : rectangle comme section d'un cube

Dessiner le profil de la section plane du cube en vraie grandeur lorsque l'arête mesure 4 cm et FI = 1 cm.

Pour obtenir le segment [AI] en vraie grandeur, dans le menu vues, choisir l'option vue standard Oxy pour faire apparaître la face ABFG du cube.

Touche V avec GéoSpace.

Pour voir la section en vraie grandeur, dans le menu vues, valider l'option vue avec un autre plan de face et choisir le plan AIJ.

Touche F avec GéoSpace.

Revenir ensuite à la vue initiale avec les touches Ctrl + F1 ou la touche W.

1.2. Carré - rectangle

La section d'un cube par un plan parallèle à une arête est un rectangle,
dans le cas où le plan est parallèle à une face, la section est un carré.

1.3. Trapèze comme section plane du cube

Section plane déterminée par un sommet et deux points sur les arêtes du cube

I et J sont deux points sur les arrêtes [BF] et [GH], arrêtes orthogonales non concourantes, ne contenant pas le sommet E.

Trouver l'intersection du plan (EIJ) avec les faces du cube.

Indications

– Mener par J, la parallèle (d) à (EI) :

Comme les faces (ABFE) et (CDHG) du cube sont parallèles, le plan (EIJ) coupe le plan (CDH) suivant cette parallèle (d) à (EI).

La droite (d), située dans la face (CDHG), coupe (CG) en K.

– La section plane EIKJ est un trapèze.

[EJ] et [IK] sont les deux autres côtés du trapèze EIKJ de bases [EI] et [JK].

Figure 3D dans GeoGebraTube : trapèze comme section plane d'un cube

Voir aussi : autre trapèze comme section par un plan contenant un sommet

1.4. Trapèzes comme sections du cube

Section plane déterminée par trois points sur des arêtes du cube

Créer les points I et J sur deux arêtes parallèles [AB], et [EF],
placer un troisième point K sur [FG] ayant le sommet F en commun avec [EF].

Construction du quatrième sommet de la section

Comme les faces (ABCD) et (EFGH) du cube sont parallèles, le plan (IJK) coupe le plan (ABC) suivant une parallèle (d) à (JK).

Trapèze lorsque la section coupe l'arête [BC]

La droite (d) coupe (BC) en L, point d'intersection du plan (IJK) avec le segment [CD].
Tracer le trapèze IJKL.

Trapèze lorsque la section coupe l'arête [CD]

La droite (d) coupe (CD) en M, point d'intersection du plan (IJK) avec le segment [CD].
Tracer le trapèze IJKM.

Figure 3D dans GeoGebraTube : deux trapèzes comme section plane du cube

1.5. Parallélogramme ou pentagone comme sections du cube

Section plane déterminée par trois points sur des arêtes parallèles du cube

Comme pour la figure précédente, mais avec le point K sur [HG] :
créer les points variables I, J et K sur les trois arêtes parallèles [AB], [EF] et [HG].

Construction automatique avec GéoSpace

Avec l'option :
créer>plan>nommé défini par trois points
appeler P le plan (IJK).

Puis définir la section avec :
créer>ligne>polygone convexe>section d'un polyèdre par un plan

Construction des autres sommets de la section « à la main »

Cas où la section coupe la quatrième arête [CD]

Trouver le point L intersection du plan (IJK) avec le segment [CD].
Tracer les segments [IJ], [JK], [KL] et [IL] et hachurer le parallélogramme IJKL.

Déplacer les points I, J ou K avec le menu piloter au clavier et faire apparaître le plus explicitement possible le parallélogramme.

Cas où la section ne coupe pas le segment [CD]

Dans le cas où le point L intersection du plan (IJK) avec la droite (CD) est à l'extérieur du segment [CD], trouver l'intersection du plan (IJK) avec une autre face du cube, par exemple avec la face ADHE si le point L est sur la droite (CD) du côté de D.

Trouver l'intersection M du plan (IJK) avec [AD] et N avec [DH]. Tracer le pentagone IJKNM.

Figure 3D dans GeoGebraTube : parallélogramme ou pentagone comme sections planes du cube

1.6. Pentagone - Problème de Bergson

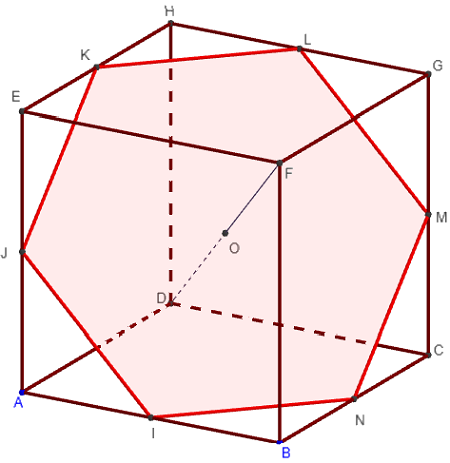
I est le milieu de [AB], J le milieu de [AE] et K le milieu de [EH]. Trouver la section plane du cube par le plan (IJK).

Voir le problème de Bergson au lycée.

Figure 3D dans GeoGebraTube : hexagone de Bergson comme section plane du cube

1.B. Sections d'un parallélépipède rectangle

Section du parallélépipède par un plan parallèle à la face AEHD.

Section par un plan parallèle à l'arête [AD].

Figure 3D dans GeoGebraTube : section plane d'un parallélépipède rectangle

La section d'un parallélépipède rectangle par un plan parallèle à une face ou une arête est un rectangle,
dans le cas où le plan est parallèle à une face, la section est un rectangle ayant les mêmes dimensions que cette face.

Travaux Pratiques 2 - Sections de pyramide

Figure 2.1 : section plane d'une pyramide par un plan parallèle à la base

Sur la hauteur [OS] placer un point variable O’.
Créer le plan Q parallèle à la base de la pyramide, passant par le point O’.
Placer les intersections du plan Q avec les arêtes et les faces de la pyramide.

Quelle est la nature du solide SA’B’C’D’ ?
Le solide ABCDA’B’C’D’ est un tronc de pyramide.

Télécharger la figure GéoSpace sec_pyr.g3w

Cas général : section plane d'une pyramide en seconde

Figure 2.2 : Tronc de pyramide

Après avoir tracé la section carrée A’B’C’D’,
effacer la grande pyramide :
avec le menu style, choisir non dessiné et montrer la pyramide SABCD.

Créer le solide (polyèdre convexe) tronc en le désignant par ses sommets ABCDA’B’C’D’.

Commandes GéoSpace
Déplacer le point A’ avec les souris ou avec les flèches du clavier
Touche P : dessiner /effacer le haut de la Pyramide
Touche F : plan (ABS) de Face
Touche W : vue initiale

Figure 3D dans GeoGebraTube : section plane et tronc d'une pyramide de base carrée

Ci-dessous : section plane d'une pyramide gauche

2.3. Volume d'un tronc de pyramide (ou d'un tronc de cône) (hors programme)

Calculer le volume de la pyramide non tronquée,
puis en déduire le volume de la partie tronquée (qui est aussi une pyramide) :

En appelant B l'aire de la grande base ABCD et b l'aire de la petite base A’B’C’D’ et h la hauteur du tronc, la formule du volume du tronc est alors :

V = [B + + b ].

Pour calculer le volume du tronc de pyramide de base carrée, avec a et b comme longueur des côtés des carrés, les anciens Égyptiens utilisaient une méthode revenant à l'emploi de la formule :

V = [a² + ab + b²].

2.4. Exemple : problème M14 du papyrus de Moscou

h = OO’ = 6, a = AB = 4, b = A’B’ = 2.

« Si on te dit : une pyramide de 6 pour la hauteur par 4 sur la base, par 2 sur le sommet.

Calcule le carré de 4, le résultat est 16.
Prends le double de 4, le résultat est 8.
Prends le carré de 2, le résultat est 4.
Tu dois additionner le 16, le 8 et le 4, le résultat est 28.
Prends de 6, il vient 2.
Prends 2 fois 28, il vient 56.

Le résultat est 56. Tu trouveras cela correct. »

V = [4² + 4 × 2 + 2²] = [16 + 8 + 4] = 2 × 28 = 56.

Télécharger la figure GéoSpace tronc_py_M14.g3w

Figure 2.5 : pyramide gauche

Recommencer avec une pyramide ABCDS de base carrée ABCD, trirectangle en A (figure GéoSpace pyram_d.g3w), telle que l'arête [AS] soit une hauteur de la pyramide.

Placer le point variable A’ sur le segment [AS] et tracer la pyramide réduite SA’B’C’D’.

Figure 3D dans GeoGebraTube : pyramide gauche de base carrée

Travaux Pratiques 3

Section et tronc de tétraèdre - Solide composite

3.1. Section plane et tronc de tétraèdre

Recommencer le TP2 précédant avec un tétraèdre régulier : dans le répertoire figures de base, choisir la figure GéoSpace tetreg.g3w.

À partir d'un point A’ situé sur l'arête [AD], trouver les traces (sur le tétraèdre) du plan passant par A’, parallèle au plan de base (ABC).

Tracer les points B’ et C’ intersections de ce plan avec les deux autres arêtes du tétraèdre.

Tronc de tétraèdre

Le tronc de tétraèdre ABCA’B’C’ est un polyèdre à 5 faces.

Le tétraèdre réduit A’B’C’D est-il régulier ?

Figure 3D dans GeoGebraTube : section plane et tronc d'un tétraèdre

3.2. Solide formé par l'assemblage d'un cube et d'une pyramide

Lanterne : solide composite

Figure 3D dans GeoGebraTube : lanterne

Dessin d'une pyramide de base carrée posée sur un cube.

Charger la figure GéoSpace de base : cube.g3w.

Tracer la médiatrice d'une des faces du cube (placer les points O au milieu de la face ABCD et H au milieu de la face A’B’C’D’, O et H sont les « milieux de diagonales »).
Placer le point S sur cette médiatrice (HO) et créer le solide l : A’B’C’D’ABCDS.

Pour le dessin du cube, l'option du menu style ne fonctionne pas.
Choisir dans le menu Éditer, l'option Éditer texte figure.

Après la définition du cube modifier la phrase Dessin de cube: opaque
Rajouter « , non dessiné »

Dessin de cube: opaque, non dessiné

Après la définition de l, insérer :

Dessin de l: opaque

Exécuter le script et valider ; sauvegarder la figure pour la réutiliser.

3.3 Obélisque

De même, réaliser un obélisque : solide formé par l'assemblage d'un tronc de pyramide de bases carrées (ou d'un parallélépipède), surmonté d'une pyramide : le pyramidion.

Le volume se calcule grâce à la formule citée après la figure 1.

WikiPédia : Obélisque

3.4 Problème bac STI (AA) 1999

Partie A

Une lanterne a la forme d'une pyramide régulière SABCD à base carrée, posée sur un cube ABCDA’B’C’D’ (figure ci-dessus).
La hauteur SH de la lanterne est de 30 cm. Soit h, en cm, la hauteur SO de la pyramide et x, en cm, la longueur de l'arête du cube.
On admet que 0 ≤ x ≤ 30.

1. Exprimer en fonction de x la hauteur de la pyramide.
2. Exprimer en fonction de x le volume V de la lanterne.

On rappelle que le volume d'une pyramide est : V = × aire de la base × hauteur

Partie B

Étude de la fonction f(x) = …

Partie C

La longueur de l'arête du cube est de 24 cm. Déterminer alors :

1. le volume V de la lanterne ;
2. la hauteur h de la pyramide ;
3. la longueur SA.

Correction bac STI : parallélépipède dans une pyramide

4. Sections planes de solides de révolution

Cylindres dont les bases sont deux cercles de centres A et B et rayon r.
L'axe (AB) des cylindres est perpendiculaire aux plans des cercles de base.

4.1. Cylindre - plan horizontal

Section par un plan perpendiculaire à l'axe (AB) du cylindre, passant par un point M de l'intervalle [AB].

La section est un cercle de centre M.

Figure 3D dans GeoGebraTube : section de cylindre

Terminale S : Volume d'un tronc de cylindre couché

4.2. Cylindre - plan vertical

Section par un plan parallèle à l'axe du cylindre, passant par les points R et S, situés sur un des cercles de base.

La section est le rectangle RSTU.

Indication : la translation de vecteur transforme le cercle de base (c) de centre A en (c’), cercle de base de centre B. Les points R et S en U et T : RSTU est un parallélogramme. Les côtés [RU] et [ST], parallèles à l'axe (AB) sont perpendiculaires à la base : un angle droit, d'où un rectangle.

figure GéoSpace seccyl1.g3w (touche 2)

4.3. Cône de révolution

La figure représente un cône de révolution. L'axe du cône est (OS). Sa hauteur OS sera notée h.
O est le centre du cercle de base (c)
et A un point de ce cercle de rayon r = OA.
Soit M un point de [OS] situé à distance h’ de S. On coupe ce cône par un plan (P) perpendiculaire à son axe en M.
Soit A’ le point du plan qui se trouve sur la génératrice [SA].
La propriété de Thalès dans le triangle SOA permet d'écrire  = ,
soit  =  d'où A’M = r × .
L'ensemble des points qui sont à la fois dans le plan et sur la surface latérale du cône est un cercle (c’) de centre M et de rayon r’, rayon donné par la formule :
r’ = r × = rk, où k =  est le rapport de réduction du cône de base le cercle (c’), de hauteur h’ avec le cône de base (c), de hauteur h.

Figure 3D dans GeoGebraTube : section de cône

4.4. Sphère

(S) est une sphère de centre O et de rayon R, (P) un plan.
H est le pied de la perpendiculaire à (P) menée par O.
OH est la distance de O à P, notée d.

On suppose que M est un point commun au plan et à la sphère et on note HM = r.

Dans le triangle OHM, rectangle en H, de la propriété de Pythagore :
HM² + OH² = OM²,
on déduit r² = R² - d².

Si d < R, l'ensemble des points d'intersection entre la sphère (S) et un plan (P) situé à une distance d de O est le cercle, du plan (P), de centre H
et de rayon r = .

Si d = R, le plan est tangent à la sphère en H.

Si d > R, le plan ne coupe pas la sphère.

Télécharger la figure GéoSpace sphere.g3w

4.5. Énigme

Par Serge Cecconi
Vercors
Bimestriel gratuit d'information du Vercors-Sud

Le demi-verre est deux fois plus petit que le verre.

Le rapport des volumes est de 2³ = 8.

Pour remplir un verre, il faut huit verres remplis à demi-hauteur.

5. Une fuite de robinet – Le Monde 27 mai-3 juin 1997

Le robinet fuit à raison d'un litre par 24 heures.
En attendant le plombier, vous placez sous la fuite un vieux bidon cubique de 30 cm d'arête ouvert sur le dessus.
Seulement voilà, la rouille y a fait exactement trois trous au centre de trois faces, le fond et deux parois contiguës.
Vous inclinez le récipient de manière à recueillir le maximum d'eau et oubliez l'incident (vous oubliez de vider la boîte).

Dans quel délai le plombier doit-il arriver pour éviter l'inondation ?

Solutions

Lorsque l'on incline le récipient de manière à rendre horizontal le plan des trois trous, on trouve une pyramide de base triangulaire.
La base est un triangle équilatéral de côté a = 30.
L'aire du triangle est égale à S = a² = 900.
La hauteur de l'eau est égale au tiers de la diagonale du cube, soit h = 10.

Le volume est donc V = S × h = 4500 cm³ ou encore 4,5 litres.

Dans cette position, on évitera l'inondation si le plombier arrive dans les trois jours.

De nombreuses lettres ont été reçues destinées à améliorer cette solution, comme celle de P. Debart et ses élèves du Caire.
Nous retiendrons particulièrement la solution de la jeune Marie-Chanel, élève de troisième au Lycée Français du Caire.

Lorsqu'on pose le cube le long d'une arête, on peut le remplir jusqu'au centre d'une face percée. Le volume d'eau qui peut séjourner dans le bidon est celui d'un prisme de base un triangle rectangle de côtés 30×15 cm et de hauteur 30 cm. Il vaut le produit de l'aire de la base (225 cm²) par la hauteur (30 cm), soit 6750 cm³, ou encore 6,75 litres.

On évitera l'inondation si le plombier arrive avant 4 jours et demi.

Élisabeth Busser et Gilles Cohen
Copyright POLE 1997
100 jeux mathématiques du Monde volume 1 - POLE 1999

Télécharger la figure GéoSpace mon_019.g3w

Table des matières

Ces figures avec GeoGebra 3D

Dans d'autres pages du site

Faire de la géométrie avec GéoSpace

GeoGebra en 5^e : Prisme - cylindre

GeoGebra en 4^e : Pyramide

Accompagnement des programmes de 3^e

Téléchargement

 Télécharger geospace_tp3.doc :
Google considère l'URL de ce document au format « .doc »comme une erreur de type "soft 404",
mais référence les copies !

Page n^o 11, réalisée le 14/3/2001
mise à jour le 23/4/2010