René Descartes Descartes et les Mathématiques

Trois des 15
problèmes de géométrie de la règle

Construction d'une droite passant par un point et l'intersection
de deux autres droites sans utiliser cette intersection impossible.

Sommaire

La perspective affranchie de l'embarras du plan géométral :
Les problèmes de la géométrie de la règle

Construction de parallèles avec une règle

Problème III
Construction avec un parallélogramme
Problème IV
Construction avec un cercle
Problème V
Intersection impossible par polaires réciproques

Jean-Henri Lambert (1728-1777)

Notes et Additions (1774) à la

Perspective affranchie de l'embarras du plan géométral

Notes et additions au troisième paragraphe

Traduction de Jeanne Peiffer
Notes de Roger Laurent et Jeanne Peiffer

Texte cité par Roger Laurenty>,
La place de J-H. Lambert (1728-1777) dans l'histoire de la perspective,
Cedic, Paris, 1987, p. 195-209 (ouvrage épuisé)

Les problèmes de la géométrie de la règle

En 1774, Jean-Henri Lambert réédite en allemand sa « Perspective affranchie
du plan géométral » qu'il avait publiée en français et en allemand en 1759.
Il complète cet ouvrage de notes additionnelles : « Anmerkungen und Zusätze ».
Ce sont ces « Notes et additions à la perspective affranchie du plan géométral »
que Jeanne Peiffer a traduit en langue française.

On y trouve les fameux quinze problèmes de la géométrie de la règle, mis en ligne
dans cette page, qui contribueront au passage de la perspective à la géométrie projective.
En effet, J.P.N. Hachette les proposera aux élèves de l'École Polytechnique dans la
« Correspondance sur l'École Polytechnique, 1804-1808 », et ces publications
n'échapperont pas à Gaspard Monge, à Jean-Victor Poncelet et à Michel Chasles.

Ce dernier en fait l'éloge dans son « Aperçu historique sur l'origine et le
développement des méthodes en géométrie » (1837) en parlant du «
célèbre Lambert, autre Leibniz par l'universalité et la profondeur de
ses connaissances, son goût pour la géométrie dont il sut faire les
plus savantes applications »

Les 15 problèmes de géométrie de la règle ont joué un rôle majeur dans le
développement et la diffusion de la perspective, et certains d'entre eux sont
encore aujourd'hui des classiques de l'enseignement de la géométrie.

Utilisation en classe - Les problèmes de Jean-Henri Lambert sont des
constructions à la règle seule qui peuvent être exploitées à tous les niveaux
de l'enseignement secondaire.
Certains sont bien connus des enseignants, comme le problème V.
Ces problèmes anciens sont à aborder dans les sections littéraires pour leurs
relations étroites avec l'histoire de l'art et de la perspective.

Problème III

Un parallélogramme ABCD étant donné, construire à l'aide d'une règle
seulement, par un point P donné, une ligne parallèle à une ligne IE donnée.

On prolonge les côtés du parallélogramme ainsi qu'une diagonale
jusqu'à ce qu'ils coupent la ligne donnée en E, F, G, H, L.
On trace arbitrairement GR issue de G et ensuite FP et EP.
Par les points d'intersection a, c, on fait passer des lignes droites issues de H, I.
Celles-ci se couperont en un point Q et PQ sera la ligne cherchée.

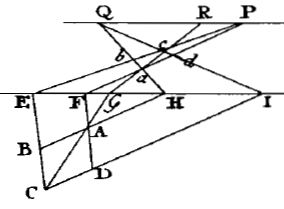
Fig. 65 - Tab. X (Notes et Add.)

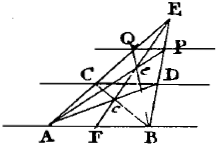
Fig. 66 - Tab. X (Notes et Add)

lambert - problèmes de géométrie de la règle - copyright Patrice Debart 2010

L'image perspective de ABCD est abcd, EI est la ligne de terre et QP l'horizon.

Si, par hasard, la droite FI est parallèle à deux côtés du parallélogramme,
alors elle sera superflue, car on pourra immédiatement indiquer
que PQ est parallèle à deux côtés du parallélogramme ;
il s'agirait alors de construire à l'aide de la règle seulement
une droite parallèle à deux autres parallèles données
et passant par un point donné.

La construction est alors la suivante: soient AB et CD les deux parallèles.
On trace par P une ligne droite BE, issue de B et dépassant P,
la ligne AE issue de A, puis AD, BC et EcF.
Finalement PA, BeQ et PQ sera la ligne cherchée.

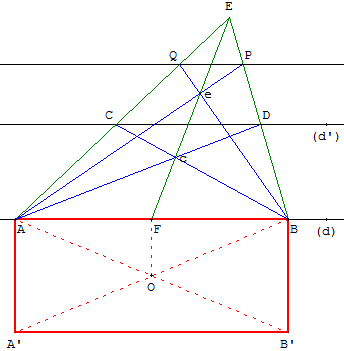
E est alors un point de l'horizon, AB la ligne de terre, CD une parallèle à celle-ci,
ABCD l'image d'un rectangle et c son centre; AE, FE et BE sont
perspectivement parallèles et par conséquent AF = FB.

Le point e représente de même le centre du rectangle AQPB, AP et QB ses diagonales,
QP le côté parallèle à la ligne de terre ; par conséquent ce parallélisme n'est
pas seulement perspectif mais aussi géométrique.

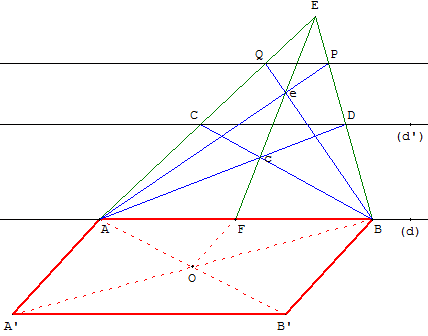
Réciproque

On voit dans la construction que AD et BC ont été tracés dans le seul but de
construire, à l'aide du point c et de la ligne EcF, le point F, qui partage AB en deux.
On peut donc considérer la réciproque du problème : AF = FB étant donnés,
tracer à l'aide d'une seule règle une ligne parallèle à AB et passant par un point P donné.
On trace BP jusqu'en un point quelconque E,
ensuite dans l'ordre EF, EA, AP, BeQ et PQ.

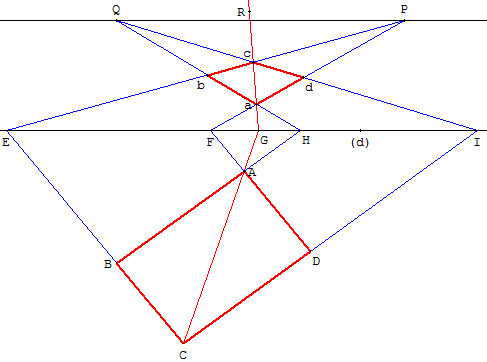
La figure 65 illustre également le problème du partage, à l'aide d'une seule règle,
d'une ligne FH dans le rapport de deux lignes EF et HI
données, une ligne PQ, parallèle à FH, étant donnée.
On trace successivement PE, PF, QH, QI et caG ; EF est à HI comme FG est à GH.

Or, si EF: FG = GH :HI est donné, on peut construire à la seule règle une ligne
parallèle à EI et passant par un point donné P. On trace GR quelconque
et ensuite PE, PF, HaQ, IeQ et finalement PQ.

Lambert donne les règles de construction d'une perspective sans justification,
mais sa méthode est tout à fait semblable aux méthodes de Brook Taylor.

Le lecteur pourra constater qu'i1 s'agit de l'étude de la conservation des propriétés
géométriques des figures par projection conique centrale, systématisée dans
le Traité des propriétés projectives des figures de J.-V. Poncelet, 1822

Problème IV

Un cercle étant donné avec son centre, abaisser une
perpendiculaire sur une ligne donnée à l'aide d'une seule règle.

On trace deux diamètres AC et BD du cercle ; A, B, C, D sont les quatre sommets,
d'un rectangle, dont on prolonge les côtés jusqu'à ce qu'ils coupent
la ligne donnée en F, G, H, I.
Sur la circonférence du cercle, on choisit un point quelconque K et
on le joint par des droites à H et à I. Ces droites coupent le diamètre AC en a et en b.
On joint G et a, F et b par des droites.
Ces dernières se coupent en c et, Kc, prolongé jusqu'en L, sera parallèle à IF.
On trace finalement le diamètre Kd, puis on trace Ld jusqu'au point M ;
LM sera perpendiculaire à FI.

Ci-dessous, figure 67 à droite : KLd est nécessairement un angle
droit puisqu'il repose sur le diamètre Kd. Par conséquent les angles
en M doivent également être droits, car KL est parallèle à FM.

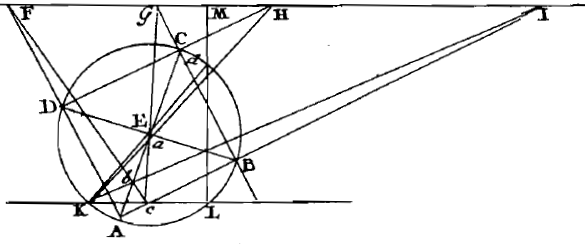
Fig.67 - Tab. X (Notes et Add.)

d étant un point du cercle, tracé de la perpendiculaire à (IF) passant par d.

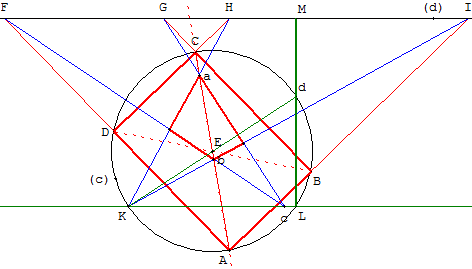
Placer un point d sur le cercle ; on trace le diamètre [dK] et on continue
la construction suivant les consignes de Lambert avec le point K trouvé.

Construire, par un point K donné,
une ligne (Kc) parallèle à une ligne (d) donnée.

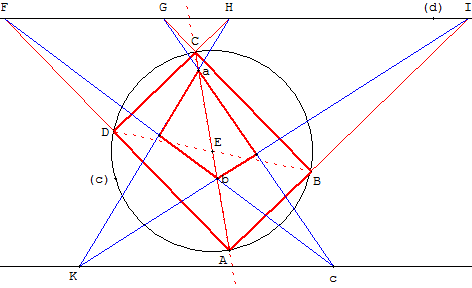
Cla parallèle Kc a été construite selon les mêmes principes que dans la figure 65.

Il suffit de déplacer le point K, dans le demi-plan ne contenant pas
le cercle par rapport à la droite (FI), pour visualiser cette construction.

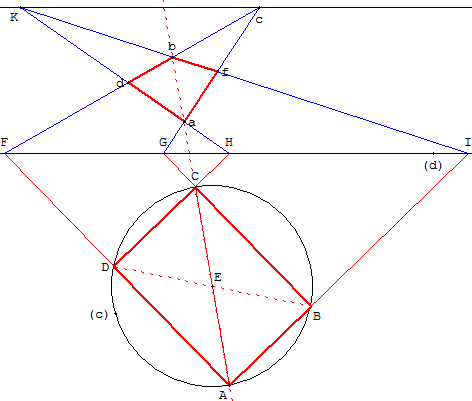
À l'aide du rectangle ABCD, on peur tracer des parallèles à ML
par des points quelconques
et, par conséquent, on peut aussi tracer avec la règle seulement
des perpendiculaires à FI passent par des points quelconques.

Tracé de la perpendiculaire (PQ) à (IF) passant par P.

La parallèle (Pc) à (IF), passant P, coupe le cercle en deux points
K et L (cette parallèle ne passe pas par le centre E).

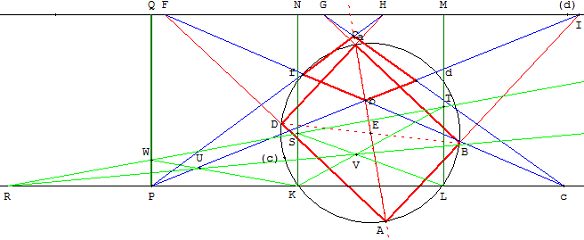
Problème V

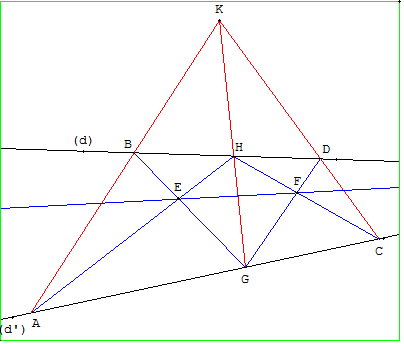
Deux droites se coupent hors de la feuille. Sans les prolonger, construire une droite passant un point E donné, concourante avec ces deux droites.

AC, BD sont des lignes qui se coupent en un point en dehors de la table,
tracer à l'aide d'une règle seulement et sans prolonger ces lignes,
une ligne passant par un point E donné et coupant BD,
AC au même point d'intersection.

On trace deux lignes AH et GB passant par E, puis on trace AB et GH
jusqu'à ce qu'elles se coupent en K. On trace KC issue de K,
puis HC et GD, EF sera la ligne cherchée.

ABHG, GHDC sont les images de rectangles,
dont les côtés convergent vers deux points de l'horizon.
E et F sont leurs centres respectifs et, par conséquent,
EF est parallèle à BD et à AC, et fuit vers le même point de l'horizon.

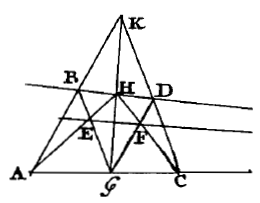
Fig. 68 - Tab. X (Notes et Add.)

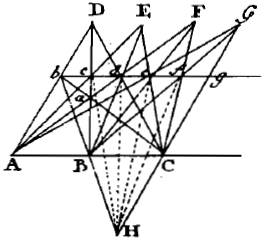
Fig. 69 - Tab. X (Notes et Add.)

Ce problème est intéressant à double titre :

• ses origines se trouvent dans la préoccupation des peintres
de tracer des parallèles en perspective sans sortir du tableau ;

• il s'inscrit dans les recherches relatives à la théorie des transversales,
pôles et polaires.
En fait, le théorème de Desargues de 1648 sur les triangles perspectifs
permet de résoudre ce problème.

Ici ABE et CDF peuvent être considérés comme deux triangles homologues
dont les côtés homologues AB et CD, BE et DF, AE et HF se coupent
respectivement en trois points R, G et H ; alignés sur l'axe d'homologie.
Alors les droites BD, EF et AC sont concourants au centre d'homologie.

Voir la construction d'un point inaccessible

Voir aussi, pour des droites parallèles (AC) et (BD),
la construction de la parallèle à (AC) passant par E.