Descartes et les Mathématiques
Cercles tangents, tangents aux côtés d'un triangle
Problème de Malfatti : une construction avec GéoPlan.
Sommaire
2. Cercles tangents aux 2 côtés d'un triangle
D'après Malfati, la source des cercles inscrits dans un triangle semble être Pappus et ces figures se retrouvent dans de nombreux Sangaku.
Voir le théorème de Descartes : 3 cercles inscrits dans un cercle
Inscrire des disques dans un cercle, un triangle, un carré ou dans un polygone régulier
1. Quatre cercles tangents, inscrits dans un triangle
À partir de la quatrième
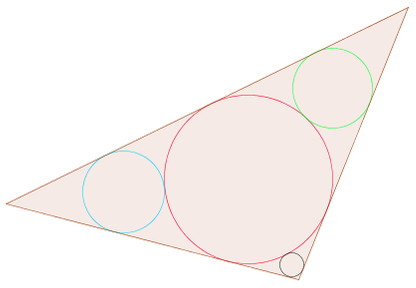
1.a. Une belle figure à construire
Un triangle étant donné, comment construire ces quatre cercles ?
Prérequis mathématiques
Définition, propriétés et construction des droites tangentes à un cercle en un point.
Définition et propriété caractéristique de la bissectrice d'un angle.
Définition et construction du cercle inscrit dans un triangle.
1.b. Un scénario possible
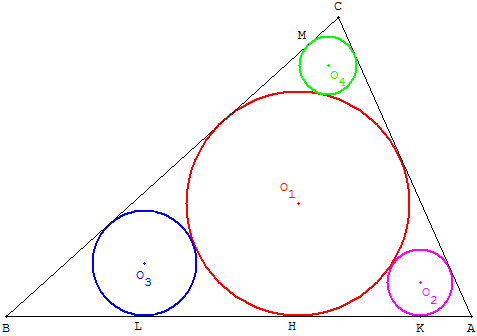
Recherche
On peut présenter la figure avec un logiciel de géométrie dynamique, en utilisant un vidéo projecteur, en plaçant quatre cercles (c1), (c2), (c3) et (c4) de centres O1, O2, O3 et O4, passant par les points H, K, L et M.
Les points H, K, L, M sont naturellement placés comme projections des centres sur les côtés du triangle ABC.
Télécharger la figure GéoPlan quatre_cercles2.g2w
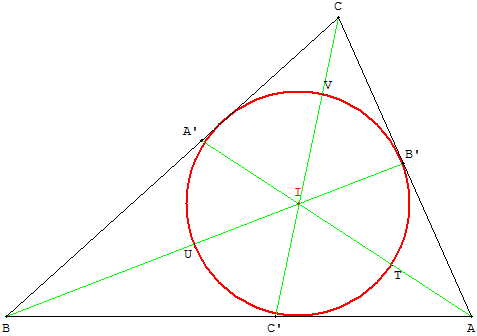
On demande alors à un élève de venir déplacer les points.
On repère rapidement les invariants de la figure et on vérifie que les centres doivent se trouver sur les bissectrices du triangle ABC.
On trace les bissectrices (touche B avec GéoPlan).
Le cercle (c1), est donc le cercle inscrit dans ABC centré en I point d'intersection des bissectrices.
En plaçant les autres centres O2, O3, O4 comme points variables sur les bissectrices du triangle ABC, on on met au défi les élèves de réaliser la même construction. C'est une première approche qui va permettre à toute la classe de rentrer dans le problème.
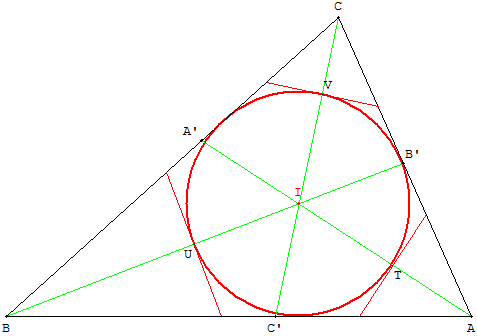
1.c. Une fois ce travail réalisé, on s'attache à en voir les limites. On propose alors la construction de la figure. Toutefois, la figure réalisée précédemment va servir d'étude. C'est en expérimentant sur cette figure que le protocole de construction va émerger.
Télécharger la figure GéoPlan quatre_cercles.g2w
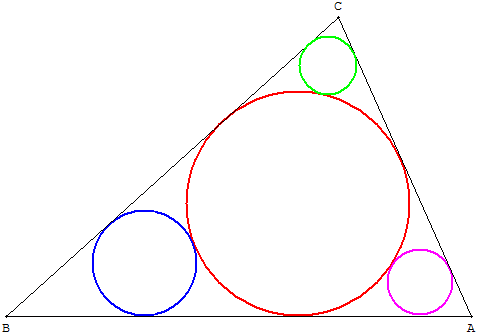
1.d. Dans cette troisième étape, on a l'occasion d'un travail différencié. On peut alors offrir des barres d'outils différentes - comme dans la plupart des logiciels de géométrie dynamique - selon les élèves : certains auront à leur disposition la construction du cercle inscrit dans un triangle ainsi que la construction du centre de ce cercle inscrit ; d'autres devront construire eux-mêmes le cercle inscrit ainsi que son centre.
2.a. Cercles tangents, tangents aux deux côtés d'un triangle
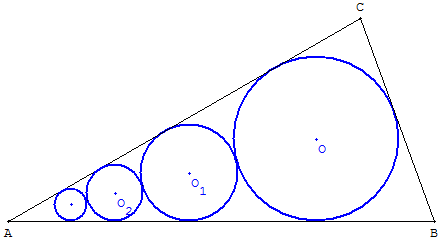
Reproduire cette figure
Construction de quatre cercles tangents aux deux côtés d'un triangle
Tracer les cercles inscrits dans les triangles formés par deux des côtés du triangle et des perpendiculaires à leur bissectrice.
Télécharger la figure GéoPlan quatre_cercles.g2w
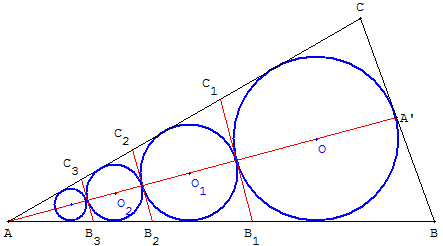
Problème de Pappus - Cercles tangents en chaîne
Relations entre les rayons des cercles en chaîne tangents deux à deux, tangents à deux cercles dont l'un est à l'intérieur de l'autre (Steiner : théorie universelle des contacts).
2.b. Deux cercles dans un triangle
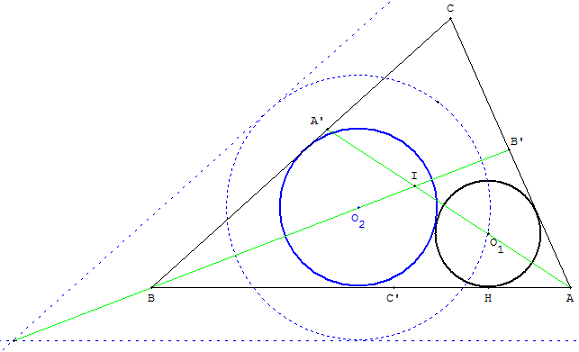
Le problème des trois cercles est un problème de contact à explorer
à partir du thème DDC : cercle tangent à deuxDroites et à un Cercle.
Ce problème a été résolu par Viète avec le recours à des droites et des cercles auxiliaires. Cette méthode sera nommée « méthode de Viète » ou des « translations parallèles ».
On donne un triangle ABC et un cercle (c1), de centre O1, de rayon r, tangent aux côtés (AB) et (AC).
On cherche et un cercle (c2), tangent aux côtés (BA) et (BC).
Utiliser la « méthode des translations parallèles » en remarquant que si le rayon du cercle (c2) cherché augmentait de r, rayon du cercle donné, le nouveau cercle passerait par le centre O1 du cercle donné et serait tangent à des droites translatées de (BA) et (BC), telle que la distance entre une droite et son image soit égale au rayon r.
Télécharger la figure GéoPlan deux_cercles.g2w
3. Cercles de Malfatti
Trois cercles tangents, inscrits dans un triangle
Sangaku
En voyant la belle figure qui accompagne l'activité proposée par Danielle, je me suis dit « Qui peut le plus, peut le moins » et j'ai donc essayé de mettre trois cercles, au lieu de quatre, dans un triangle.
C'est le problème de Malfatti : il s'agit de construire trois cercles, inscrits dans les angles d'un triangle, et tels qu'ils soient tangents deux à deux.
En 1803, Giovanni Francesco Malfatti a posé le problème de déterminer les trois colonnes circulaires de marbre, éventuellement de différentes tailles qui, sculptées dans un prisme droit triangulaire, auraient la plus grande coupe transversale totale possible.
C'est équivalent à la recherche de trois cercles de taille maximum qui peuvent être inscrits à l'intérieur d'un triangle rectangle de n'importe quelle forme, sans se chevaucher. Ce problème est maintenant connu comme le « problème de marbre ».
Malfatti a donné comme solution les « trois cercles Malfatti », tangents l'un à l'autre et à deux côtés du triangle et il a démontré analytiquement l'existence de ces trois cercles.
Une solution purement géométrique a été donnée, sans preuve, par Steiner en 1826.
En 1930, il a été montré que les cercles Malfatti n'étaient pas toujours la meilleure solution. Alors Goldberg (1967) a montré que, pire encore, ils ne sont jamais la meilleure solution. Ogilvy (1990) et Wells (1991) illustrent des cas spécifiques où les solutions alternatives sont clairement optimales.
D'après MathWorld.
Recherche avec GéoPlan
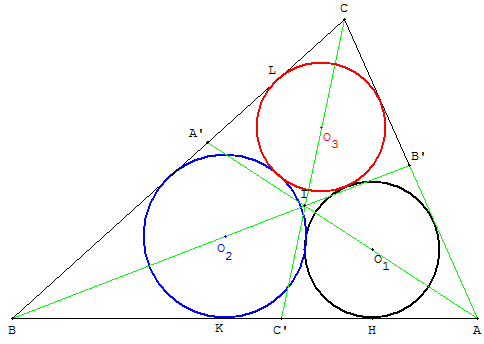
Les TICE permettent une première recherche en plaçant trois cercles (c1), (c2) et (c3) de centres O1, O2 et O3, passant par les points H, K et L.
Les points H, K, L sont naturellement placés comme projections des centres sur les côtés du triangle ABC.
On vérifie rapidement que les centres doivent se trouver sur les bissectrices du triangle ABC.
En déplaçant les centres O1, O2, O3, comme points variables sur les bissectrices du triangle ABC, on trouve trois cercles : (c1), tangents aux côtés (AB) et (AC) ; (c2) tangent aux côtés (BA) et (BC) et (c3) tangent aux côtés (CA) et (CB) ; solution approchée du problème.
Télécharger la figure GéoPlan trois_cercles2.g2w
Une piste de recherche en s'affranchissant de la contrainte : (c2) et (c3) tangents
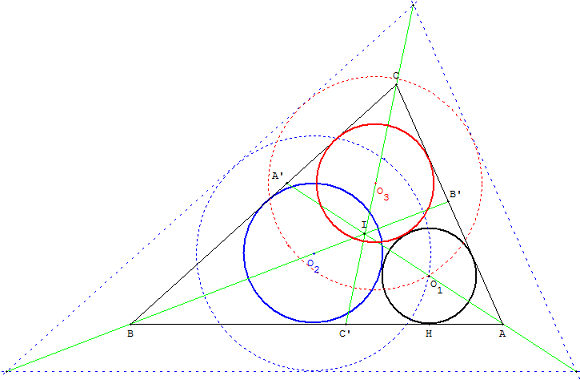
On donne un triangle ABC et un cercle (c1), de centre O1, de rayon r, tangent aux côtés (AB) et (AC).
Avec la « méthode des translations parallèles » vue au paragraphe précédent, on place un cercle (c2), tangent à (c1) et aux côtés (BA) et (BC) ainsi qu'un cercle (c3), tangent à (c1) et aux côtés (CA) et (CB).
Télécharger la figure GéoPlan trois_cercles.g2w
Vers la solution avec le logiciel
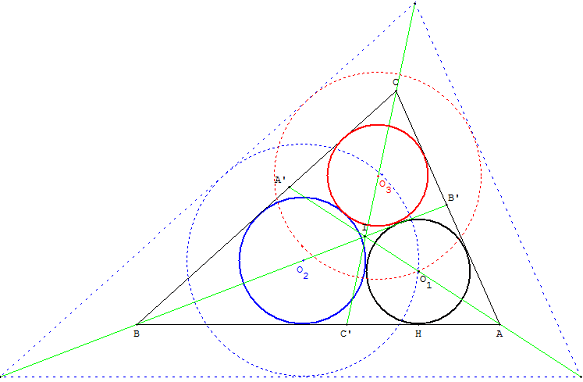
Le problème n'a plus qu'un degré de liberté. En déplaçant le centre O1, on trouve la solution où les cercles (c2) et (c3), sont tangents.
On peut penser que cette preuve par GéoPlan est une démonstration analytique.
Le traité de géométrie de Rouché et De Comberousse donne une construction à la « règle et au compas » de cette position de telle manière que la droite joignant les points d'intersection des cercles (c2) et (c3) soit tangente aux cercles inscrits dans les triangles IAB ou IAC. Il suffit de trouver un des points de contact situé sur la perpendiculaire passant le centre d'un des cercles inscrits.
Le triangle O1O2O3, formé par les centres des cercles de Malfatti, est le triangle de Malfatti du triangle ABC.
Voir ses propriétés dans : trois cercles tangents.
Voir carrés de Malfatti : inscrire trois carrés dans un triangle donné
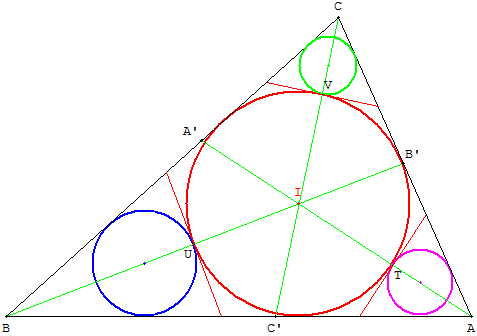
4. Construction exacte de Steiner (1826)
Rouché Eugène et De Comberousse Charles – Traité de géométrie - 1900 - Éditions Jacques Gabay - 1997
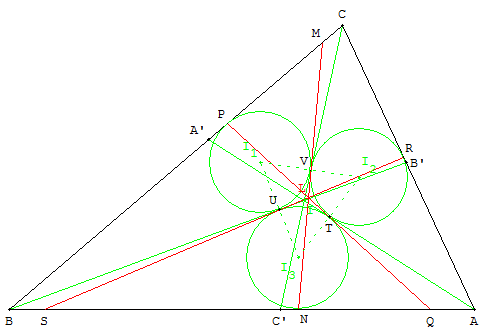
Recherche des tangentes communes
I étant le centre du cercle inscrit, tracer les cercles inscrits dans les triangles IBC, IAC et IAB. Les trois bissectrices sont tangentes intérieures à ces cercles pris deux à deux.
Mener les trois autres tangentes intérieures qui coupent les bissectrices en U, V et T situés sur les lignes des centres des cercles.
Pour cela, soit U le point d'intersection des droites (I1I3) et (BB’) et U3 le point de contact de la tangente (BB’) avec le cercle inscrit dans IAB. Ce cercle coupe le cercle de diamètre [UI3] en U3 et U1.
La droite (UU1) est la deuxième tangente issue de U, qui coupe le triangle en R et S (tracé pratiquement impossible sans logiciel).
Recommencer avec T.
Ces tangentes sont sécantes en L qui est le centre radical des cercles solutions. Cela permet de tracer la dernière tangente simplement comme droite (VL).
Solution
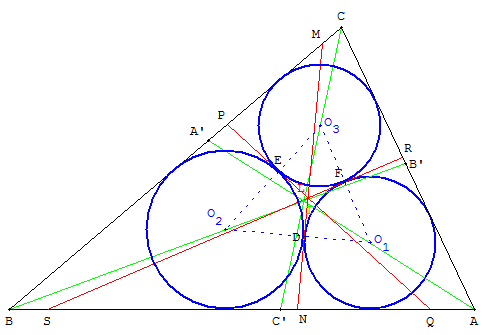
Les cercles inscrits dans les triangles ayant comme côté une de ces tangentes et deux des côtés du triangle ABC, sont les cercles cherchés
Le triangle O1O2O3 est le triangle de Malfatti de ABC.
Le cercle circonscrit au triangle DEF, de centre L, est inscrit dans le triangle O1O2O3.
Télécharger la figure GéoPlan trois_cercles4.g2w
Table des matières
Dans d'autres pages du site
Construction de cercles problèmes de contact
Troisième : Problèmes d'optimisation
Seconde : Problèmes d'optimisation
Trois cercles égaux à l'intérieur d'un triangle
Google friendly
|
|
Page no 156 créée le 25/5/2010 |