Descartes et les Mathématiques
La planche à clous comme geoplan
Activités avec le geoplan pour construire des objets de la géométrie.
Sommaire
1. Le geoplan
5. Théorème de Pythagore : figure du moulin à vent
Sur tablette numérique ou smartphone, bascule automatique vers la version mobile
Dans d'autres pages du site
Calculs d'aire - Théorème de Pick
Parabole dans un geoplan 5 × 5
Aire d'un quadrilatère dans un geoplan 5 × 5
GeoGebraBook : la planche à clous comme geoplan
C'est quoi un geoplan ?
1. Le geoplan
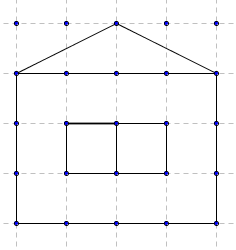
Le geoplan, inventé par Caleb Gattegno, est un carré de bois de 30 cm de côté où sont plantées 25 pointes. Il est structuré par un réseau de (4 × 4) carrés isométriques.
On peut aussi envisager des planchettes à 9 ou 16 clous…
Les clous permettent de tendre des élastiques et de former ainsi des figures représentant des segments, des angles, des polygones, etc.
Le geoplan permet la création de multiples situations de géométrie, avec comme unité de longueur la distance entre 2 clous consécutifs situés sur une ligne parallèle aux bords du geoplan, et comme unité d’aire, l'aire d'un petit carré du réseau.
On alternera la construction avec les élastiques, le dessin sur un quadrillage et le travail sur ordinateur.
Comme ci-contre, dès la maternelle, on peut commencer par des créations libres.
geoplan vierges
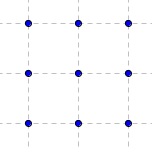
geoplan 3 × 3
9 points ; 4 unités d'aire
geoplan 4 × 4
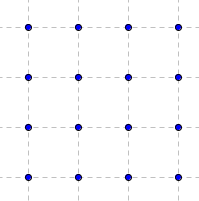
16 points ; 9 unités d'aire
geoplan 5 × 5
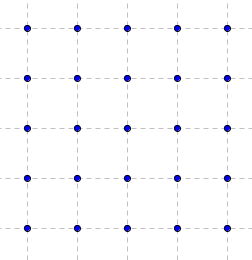
Figure interactive dans GeoGebraTube : geoplan 3 sur 3 vierge,
2. Les figures de base du geoplan
La géométrie avec une planche à clous
2.a. geoplan 3 × 3
Découpage des polygones du geoplan 3 × 3
Dans le geoplan 3 × 3, tous les triangles et les polygones (non-croisés) peuvent être obtenus à partir de deux types de triangles de base le demi-carré ABC et le triangle DEF (ou son symétrique).
Il est possible de calculer l'aire des figures avec cette décomposition en carrés et demi-carrés et en triangles de base, d'aires un demi.
Triangles de base
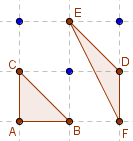
Aire(ABC) = Aire(DEF) = 0,5.
Un autre triangle
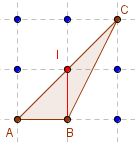
Aire(ABC) = Aire(ABI) + Aire(IBC) = 1.
Deux triangles du geoplan 3 × 3 ; triangle dans le geoplan 3 × 3
2.b. Approche de la notion d'aire et de périmètre du triangle
Comment calculer l'aire d'un triangle inscrit dans un carré (un carré ou un rectangle du geoplan).
Figure interactive dans GeoGebraTube : aire d'un triangle du geoplan 5 sur 5
Diverses possibilités d'étude :
• Étude d'aire avec GeoGebra
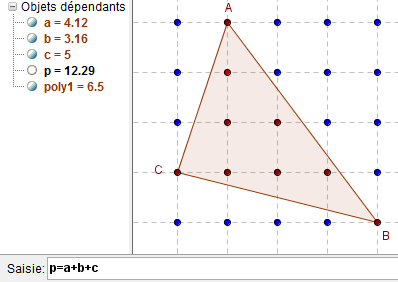
En cliquant successivement les sommets B, C puis A, dans cet ordre, et en terminant par le point B, GeoGebra crée le triangle poly1 et renvoie l'aire de ce du triangle dans la fenêtre algèbre.
Les côtés sont alors a = BC, b = CA et c = AB.
En validant la formule p=a+b+c dans la ligne de saisie, on obtient une valeur approchée du périmètre.
• Par déformation en triangles d'aires équivalentes :
Méthode utilisable lorsque des éléments de la figure sont parallèles aux bords du geoplan.
•Procéder par addition en décomposant la figure en éléments primaires (impossible sur cette figure).
• Procéder par soustraction
en enlevant à l'aire du grand carré, les aires des triangles ou polygones extérieurs à la figure.
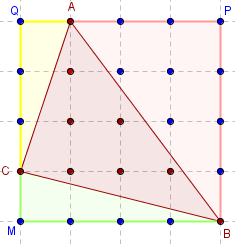
Aire(ABC) = Aire(MBPQ) – { Aire(MBC) + Aire(PAB) + Aire(QAC) }
Aire(ABC) = 16 – {2 + 6 + 1,5} = 6,5.
• Utiliser la formule de Pick (cf. ci-dessous).
Aire(ABC) = i + 
b – 1, où i = 6 est le nombre de points de la grille à l'intérieur du triangle
et b = 3 le nombre de points sur le bord du triangle,
- soit Aire(ABC) = 6 + 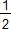× 3 – 1 = 6,5.
2.c. Figures, dans les geoplan 3 × 3 et 5 × 5
Figures d'aire maximale, en évitant, le plus possible, les côtés parallèles aux bords du geoplan.
Triangle
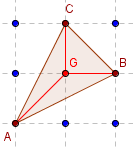
Aire(ABC) = 1,5.
Le triangle est la réunion de trois triangles d'aires 0,5 : le demi-carré GBC et les deux triangles de base GAB et GAC.
Carré d'aire égale à 2
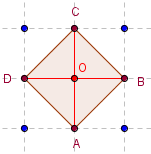
Aire(ABCD) = 4 × = 2.
Les diagonales se coupent en leur milieu O, sont de même longueur et sont perpendiculaires.
Trapèze isocèle
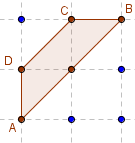
Aire(ABCD) = 2 – 0,5 = 1,5.
(AB)//(DC) et AD = BC.
Parallélogramme
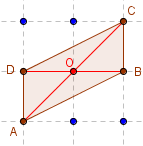
base × hauteur = AD × DB = 2.
Aire(ABCD) = 2.
Avec les diagonales, décomposer en deux demi-carrés, plus deux triangles de base OAB et OCD.
Triangle du geoplan 4 × 4
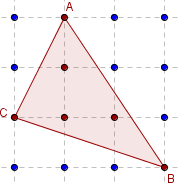
Aire(ABC) = 3,5.
Aire(ABC) = 9 – {1+3+1,5} = 3,5.
Carré d'aire égale à 5
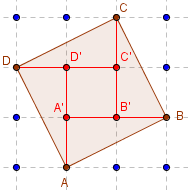
Le carré ABCD, formé du carré central A’B’C’D’ unitaire, et de quatre triangles rectangles AA’B, BB’C, CC’D, DD’A d'aires 1.
Aire(ABCD) = 1 + 4 × 1 = 5.
Trapèze isocèle particulier
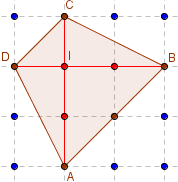
(AB)//(DC) et AD = BC.
Aire(ABCD) = AC × BD = 4,5.
Ici, les diagonales sont de même longueur et perpendiculaires ; ABCD est aussi un pseudo-carré.
Quadrilatère croisé
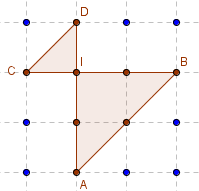
Aire(ABI) = 2 ;
Aire(CDI) = 0,5 ;
Aire(ABCD) = 2 + 0,5 = 2,5.
Quatre carrés
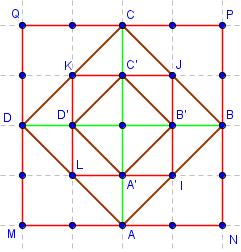
Aire(MNPQ) = 16,
Aire(ABCD) = 8,
Aire(IJKL) = 4,
Aire(A’B’C’D’) = 2.
Carré d'aire égale à 10
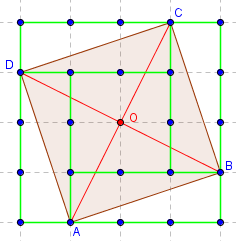
Aire(ABCD) = 4 + 4 × 1,5 = 10,
Aire(ABCD) = 16 – 4 × 1;5 = 10.
L'aire est obtenue en ajoutant ou en retranchant, à l'aire d'un carré, les aires de quatre triangles rectangles, d'aires 1,5.
Rectangle
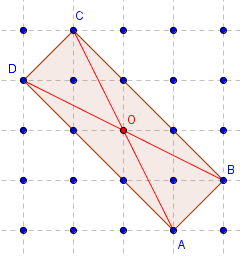
Aire(ABCD) = 6.
Les diagonales sont de même longueur.
Rectangle dans le geoplan 5 × 5
Rectangle dans le geoplan 3 × 3
Voir le rectangle au collège
Parallélogramme
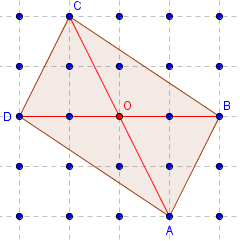
Aire(ABCD) = 8.
Le nombre impair de points sur les diagonales permet de vérifier qu'elles se coupent en leur milieu.
Aux isométries près, on trouve 8 familles de triangles différents dans le geoplan 3 × 3 et 29 familles de triangles dans le geoplan 4 × 4 :
voir le site de Jean-Louis Sigrist
2.d. Réseau de triangles équilatéraux
Dans les geoplans précédents, il n'est pas possible de tracer un triangle équilatéral.
Pour cela, on peut utiliser une planche à mailles triangulaires :
Réseau triangulaire
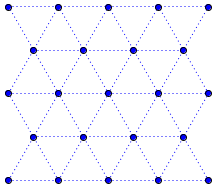
Figure interactive dans GeoGebraTube : réseau triangulaire
Triangle équilatéral
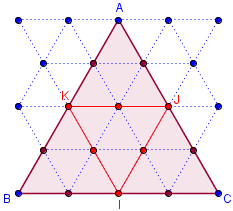
Hexagone
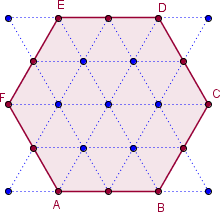
Réseau d'hexagones
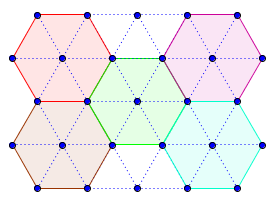
Figure interactive dans GeoGebraTube : hexagone_reseau
3. Autres quadrilatères
Trapèze
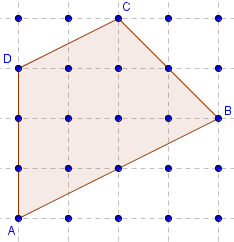
Aire(ABCD) = 9.
(AB)//(DC)
Trapèze rectangle
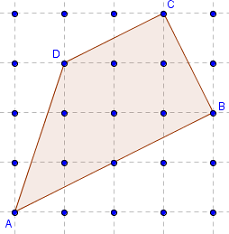
Aire(ABCD) = 7,5.
(AB)//(DC) et (BC) est perpendiculaire à (AB) et à (CD).
Trapèze isocèle
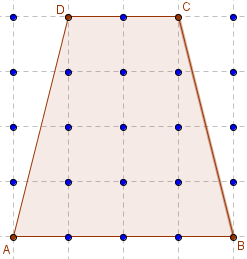
Aire(ABCD) = 12.
(AB)//(DC) et AD = BC.
Trapèze isocèle particulier
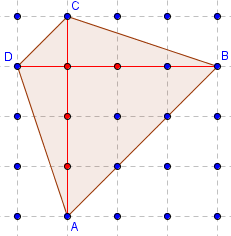
Aire(ABCD) = AC × BD = 8.
Ici, dans ce cas particulier, les diagonales sont perpendiculaires et de même longueur ; ABCD est aussi un pseudo-carré.
Losange
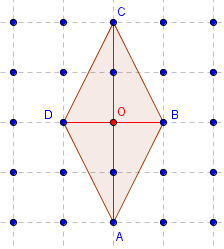
Aire(ABCD) = AC × BD = 4.
Les diagonales se coupent en leur milieu O et sont perpendiculaires.
Autre losange
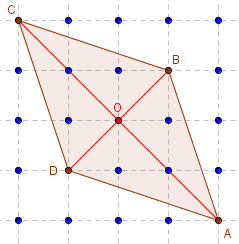
Aire(ABCD) = AC × BD = 8.
Cerf-volant (géométrie)
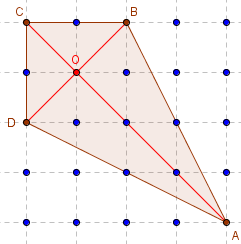
Aire(ABCD) = AC × BD = 8.
Les diagonales sont perpendiculaires et leur point d'intersection O est le milieu d'une des deux diagonales.
Cerf-volant pseudo-carré
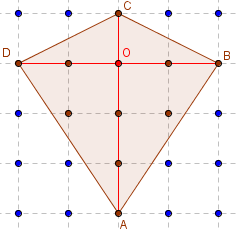
Aire(ABCD) = AC × BD = 8.
Ici, les deux diagonales perpendiculaires sont de même longueur, ABCD est aussi un pseudo-carré
Quadrilatère orthodiagonal
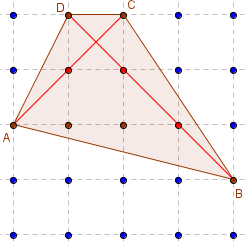
Aire(ABCD) = AC × BD = 6.
Les diagonales se coupent à angle droit.
Pseudo-carré
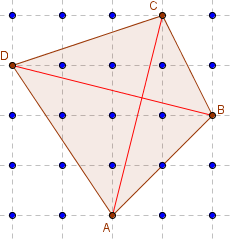
Aire(ABCD) = AC × BD = 8,5.
Les diagonales sont perpendiculaires et de même longueur.
Fer de lance
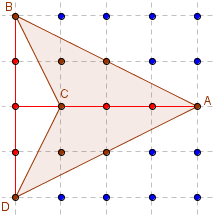
Aire(ABCD) =
Aire(ABD) - Aire(CBD) = 6.
Exemple de quadrilatère non convexe.
Quadrilatère croisé
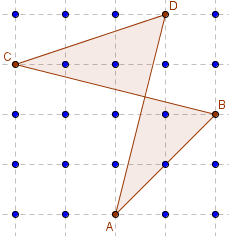
Pas plus que GeoGebra, je ne sais pas calculer cette aire.
Aire d'un quadrilatère inscrit dans un carré
Cas général : à l'aire du carré, retrancher l'aire des triangles bordant le quadrilatère (convexe).
4. Théorème de Pick pour le calcul d'une aire
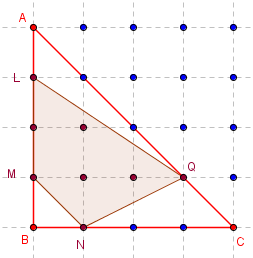
Figure extraite de l'article aire d'un quadrilatère dans un geoplan 5 × 5
On peut calculer l'aire du quadrilatère MNQL avec la formule de Pick
Aire(MNQL) = i + b – 1,
où i = 3 est le nombre de points de la grille à l'intérieur du quadrilatère et b = 5 le nombre de points sur le bord du quadrilatère,
soit Aire(MNQL) = 3 + × 5 – 1 = 4,5.
Figure interactive dans GeoGebraTube : transformer un quadrilatère en triangle dans le geoplan
Cocher la case geoplan 5 × 5
5. Théorème de Pythagore
Figure d'Euclide dite du « moulin à vent »
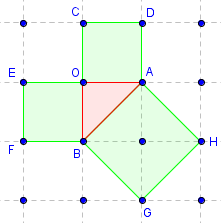
Soit OAB un triangle rectangle en O, tel que :
a = OA = 1 ; b = OB = 1;
Aire(OACD) = a2 = 1 ; Aire(OEFB) = b2 = 1.
c = AB ; le carré ABGH, formé de quatre demi-carrés unitaires, a pour aire c2 = 4 × = 2 ;
on a bien la propriété de Pythagore : a2 + b2 = c2, d'où c = 
.
Figure interactive dans GeoGebraTube : moulin à vent du geoplan 4 × 4
Voir : théorème de Pythagore et Euclide
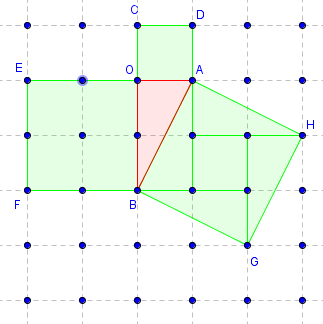
Soit OAB un triangle rectangle en O, tel que :
a = OA = 1 ; b = OB = 2 ;
Aire(OACD) = a2 = 1 ; Aire(OEFB) = b2 = 4.
c = AB ; le carré ABGH, formé d'un carré central unitaire, et de quatre triangles rectangles d'aire 1, a pour aires c2 = 5 ;
on a bien la propriété de Pythagore : a2 + b2 = c2, d'où c = 
.
Figure interactive dans GeoGebraTube : moulin à vent du geoplan 6 sur 6
Retrouver ces carrés dans la page carré d'aire 5
et dans GeoGebraTube : moulin à vent d'Euclide dans un quadrillage
Table des matières
Google friendly
Bibliographie : APMEP – Plot no 32 – Quatrième trimestre 2010 – « Le geoplan, alias la planche à clous » – Renée Vanderstraeten
Méthode Heuristique Math géométrie : le-géoplan
Page no 196, réalisée le 13/11/2012