Descartes et les Mathématiques
Activités de l'espace en première
Exercices de géométrie dans l'espace au lycée : droite parallèle à un plan, interaction de l'espace et du plan…
Sommaire
1. Intersection de plans (dans une pyramide)
2. Section plane d'une pyramide
3. Intersection d'une droite et d'un cube
4. Barycentre et tétraèdre : alignement dans l'espace
5. Utilisation de l'espace dans la résolution d'un problème plan
6. Construction dans l'espace utilisant une configuration du plan
8. Les ambiguïtés de la perspective cavalière
9. Intersection de deux plans - Section plane d'un parallélépipède
GeoGebra en 2nde:
Droite parallèle à un plan dans un cube
Sur tablette ou smartphone, bascule automatique vers la version mobile
Programme de 1ère S (2009)
La géométrie dans l'espace est source de situations permettant de mettre en œuvre de nouveaux outils de l'analyse ou de la géométrie plane, notamment dans des problèmes d'optimisation.
Malgré cet entête, la géométrie dans l'espace a disparu du nouveau programme de 2009 !
1. Intersection de plans (autour d'une pyramide)
SABCD est une pyramide régulière de sommet S, de base le carré ABCD, de côté AB = 4 cm, telle que le triangle ASC soit équilatéral.
1.a. Soit O le centre du carré ABCD. Déterminer l'intersection des plans (SAC) et (SBD).
Étudier les triangles SAC et SBD en déduire que (SO) est la hauteur de la pyramide.
1.b. Calculer AC et OS.
Soit I le point de la hauteur OS équidistant de A et de S. Calculer SI.
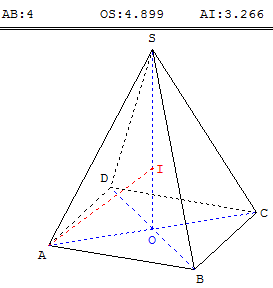
Indications : a = AB = 4 ; AC = AS = a 
;
OS = 
et SI = 
(le point I est le centre de gravité du triangle SAC).
Figure 3D dans GeoGebraTube : pyramide de base carrée - plan diagonal
Cocher la case triangle rectangle isocèle
4.c. Déterminer l'intersection des plans (SAB) et (SCD).
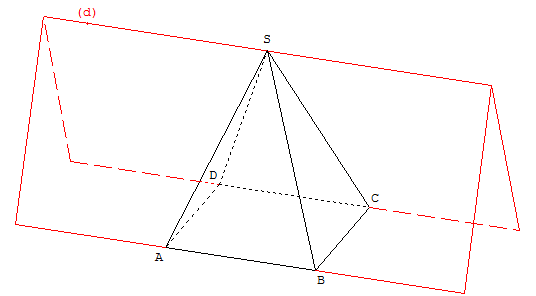
D'après le théorème du toit, la droite (d), intersection des plans (SAB) et (SCD), est parallèle aux côtés (AB) et (CD).
Télécharger la figure GéoSpace pyramide_inter_plan.g3w
2. Section plane d'une pyramide
SABCD est une pyramide de sommet S et de base le carré ABCD.
Les points I et J appartiennent aux arêtes [SA] et [SB].
Le point K appartient à l'arête [SC].
Étudier la section de la pyramide par le plan (IJK).
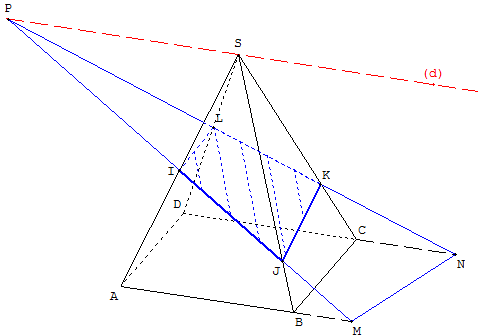
Soit (d) la parallèle à (AB) passant par S.
Si (IJ) n'est pas parallèle à (AB), la droite (IJ) coupe (d) en P et (AB) en M.
Éventuellement, la droite (PK) coupe (SD) en L et (CD) en N.
Sur cette figure la section est le quadrilatère IJKL.
Télécharger la figure GéoSpace pyramide_section_plane.g3w
Le point Q appartient à la face SCD.
Étudier la section de la pyramide par le plan (IJQ).
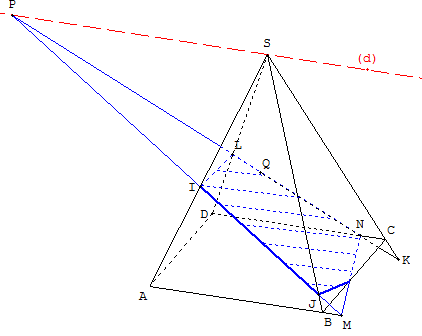
Éventuellement, la droite (PQ) coupe (SC) en K, (SD) en L et (CD) en N.
Sur cette figure la section est le quadrilatère IJKL.
Télécharger la figure GéoSpace pyramide_section_plane.g3w
3. Intersection d'une droite et d'un cube
I et K sont deux points de la face (EFGH) d'un cube et J un point de la face (ABFE).
Par K passe la droite (d) parallèle à (IJ).
Trouver une construction du point L intersection de la droite (d) et du plan (ABF).
Exercice
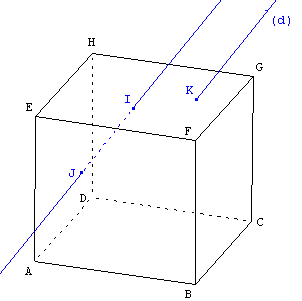
Télécharger la figure GéoSpace cube_dr.g3w
Solution
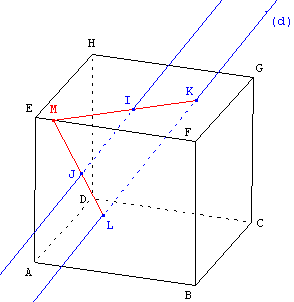
Tracer le point M (s'il existe), intersection de la droite (IK) avec l'arête (EF).
Le point L est l'intersection de (d) et de (MJ).
4. Barycentre et tétraèdre : alignement dans l'espace
ABCD est un tétraèdre.
Soit I le milieu de l'arête [AD],
G le centre de gravité du triangle ABC,
E le point tel que le quadrilatère BDCE soit un parallélogramme.
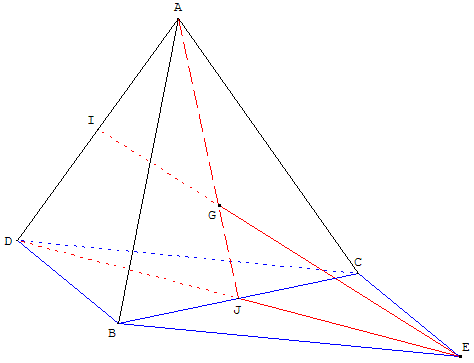
4.a. Déterminer des nombres entiers b, c et d tels que le point E soit le barycentre des points pondérés (B, b) ; (C, c) et (D, d).
La somme de vecteurs 
+ 
est représentée par la diagonale 
du parallélogramme :
+ = + 
= .
+ – = 
,
donc, en choisissant 1 pour b, les coefficients sont :
b = 1, c = 1 et d = − 1.
4.b. Démontrer que 
+ + – – = .
En ajoutant et en retranchant à l'égalité + – = ,
on montre que + + – – = .
4.c. Déduire de la question précédente que la droite (GI) coupe le plan (BCD) en E.
G est le centre de gravité du triangle ABC on peut donc écrire l'égalité vectorielle de Leibniz :
3
= + + .
I est le milieu de l'arête [AD], donc d'après le théorème de la médiane : 2 
= – .
L'égalité de la question précédente devient : 3 – 2 = ,
les points E, G et I sont alignés et la droite (GI) coupe le plan (BCD) en E.
4.d. Préciser la position de E par rapport aux points G et I.
D'après l'égalité de la question précédente, E est le barycentre de (G, 3) et (I, –2), donc 
= − 2 
.
Télécharger la figure GéoSpace tet_alig.g3w
Centre de gravité d'un tétraèdre, voir : isobarycentre de quatre points
5. Perspective de centre O
Utilisation de l'espace dans la résolution d'un problème plan
Exercice
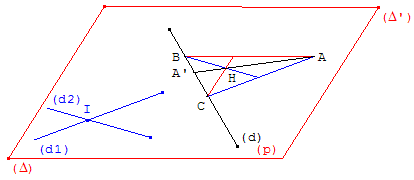
Étant donné dans un plan trois droites (d1), (d2), (d3) distinctes et concourantes en O et trois points A, B, C distincts n'appartenant pas à ces droites, construire un triangle MNP tel que chaque côté contienne un des trois points et que chaque sommet soit sur une des trois droites.
Démonstration « par le relief »
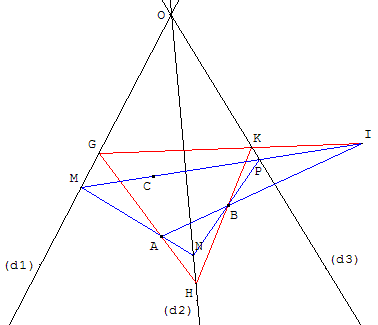
La figure ci-contre peut-être considérée comme la représentation d'un trièdre de sommet O et d'arêtes (d1), (d2), (d3). Les points A, B, C appartenant respectivement aux plans (d1, d2), (d2, d3), (d1, d3). La construction demandée revient à déterminer l'intersection du plan (ABC) et du trièdre (O, d1, d2, d3).
Pour cela, à partir d'un point G, on va montrer que le triangle MNP peut être considéré comme la vue en perspective d'un triangle GHK, situé dans le plan (GAB), les plans de ces deux triangles ayant la droite (AB) en commun. Sur cette droite le point I est l'intersection des plans des deux triangles avec le plan (d1, d3).
G étant un point de (d1), on trace (GA) qui coupe (d2) en H, puis (HB) qui coupe (d3) en K.
Les points A et B situés sur les droites (GH) et (KH) appartiennent au plan (GHK), ainsi que la droite (AB). Les droites (AB) et (GK) du plan (GHK) se coupent en I.
Les points G et K situés sur les droites (d1) et (d3) appartiennent au plan (d1,
d3), la droite (GK) est dans ce plan et en particulier le point I. Par hypothèse C aussi un point du
plan (d1, d3), la droite (CI) située dans ce plan coupe (d1) en M
et coupe (d3) en P, qui sont deux des sommets du triangle cherché. Le troisième sommet N sur (d2) s'obtient en traçant (MA) et (PB).
Télécharger la figure GéoSpace pb_plan.g3w
Théorème de Desargues : plan projectif
Perspective et résolution d'un problème plan
Droite menée à partir d'un point de concours inaccessible
Joindre deux points d'une droite avec une règle trop courte
6. Construction dans l'espace utilisant une configuration du plan
Exercice
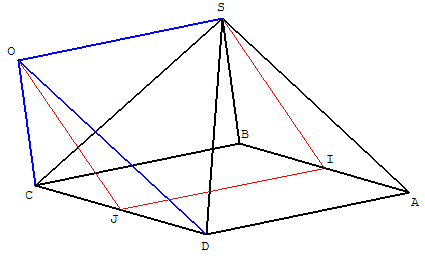
Dans un plan (p), tracer la perpendiculaire à une droite (d) à partir d'un point A.
Solution
Dans une perspective cavalière, le plan (p) est figuré par l'image d'un rectangle sous forme d'un parallélogramme. Les côtés (Δ) et (Δ’) sont perpendiculaires.
On suppose que dans le plan (p) on connaît l'image de deux droites perpendiculaires (d1) et (d2),
non parallèles à (Δ) et (Δ’), représentées, en général, par des segments non perpendiculaires.
La construction utilise les hauteurs et l'orthocentre d'un triangle.
On mène par le point A les parallèles à (Δ) et (d1) qui coupent la droite (d) respectivement en B et C.
La parallèle à (Δ’) passant par C est une hauteur du triangle ABC, de même la parallèle à (d2) passant par B. Ces deux hauteurs se coupent en H, orthocentre du triangle ABC. La droite (AH), troisième hauteur du triangle, est la perpendiculaire à (d) menée par A.
Télécharger la figure GéoSpace dr_perpendiculaire.g3w
7. Pyramide et tétraèdre
Solide composite : prisme oblique
On dispose d'une pyramide à base carrée d'arêtes de longueur a
et d'un tétraèdre régulier de même longueur d'arêtes. On colle ces deux solides en faisant coïncider deux de leurs faces triangulaires.
On obtient ainsi un nouveau polyèdre.
Combien a-t-il de faces ?
Quelle est la nature de ce polyèdre ?
Indications
Soit I et J les milieux des côtés [AB] et [CD] de la base (ABCD) de la pyramide SABCD de sommet S.
Montrer que le sommet O du tétraèdre OCDS appartient au plan médiateur (IJS) de la pyramide.
En déduire que le quadrilatère IJOS est un parallélogramme ; les points O, S, A et D sont coplanaires ainsi que les points O, S, B et C.
Le polyèdre a cinq faces : un carré, deux losanges et les deux triangles équilatéraux SAB et ODC. C'est un prisme oblique. Toutes les arêtes sont de même longueur a.
Télécharger la figure GéoSpace pyr_tet.g3w
8. Les ambiguïtés de la perspective cavalière
8.a. Deux droites dans un cube
IREM de Poitiers
Bulletin inter IREM 1986
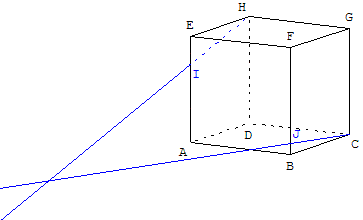
Les droites (IH) et (JC) sont-elles sécantes ?
Télécharger la figure et vérifier ce que dit GéoSpace si l'on voulait construire un point d'intersection.
Télécharger la figure GéoSpace cub_secante.g3w
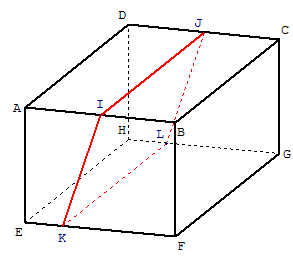
8.b. Un quadrilatère dans un cube
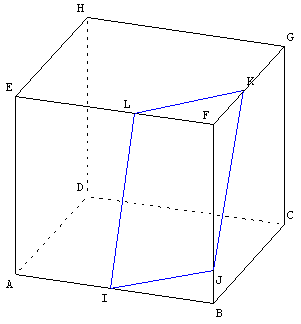
Que dire du quadrilatère IJKL ?
Rien, c'est une figure gauche non située dans un plan. Surtout pas un parallélogramme.
Télécharger la figure GéoSpace cub_quadri.g3w
8.c. Incidence fausse de deux droites et deux plans
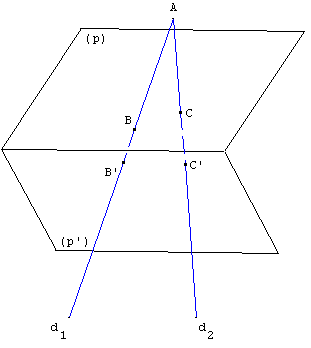
Les droites (d1) et (d2), sécantes en A, coupent le plan (p) en B et C, et le plan (p’) en B’ et C’.
Ce dessin n'est pas exact. Le point C’, par exemple, est mal placé.
Retrouver sa position sur (d2) à partir du point I intersection de la droite (BC) et de la droite frontière de (p) et (p’).
Télécharger la figure GéoSpace dr_secantes.g3w
8.d. Vertical ou horizontal ?
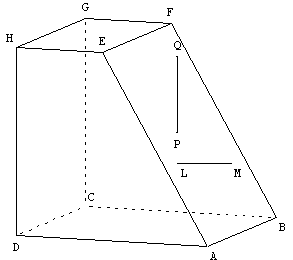
Dans le plan (ABF), la droite (LM) est-elle horizontale ?
La droite (PQ) est-elle verticale ?
Tracer une droite horizontale de ce plan.
Peut-on trouver une droite verticale dans ce plan ?
Télécharger la figure GéoSpace pave_demi_droit.g3w
Voir : perdu dans l'espace
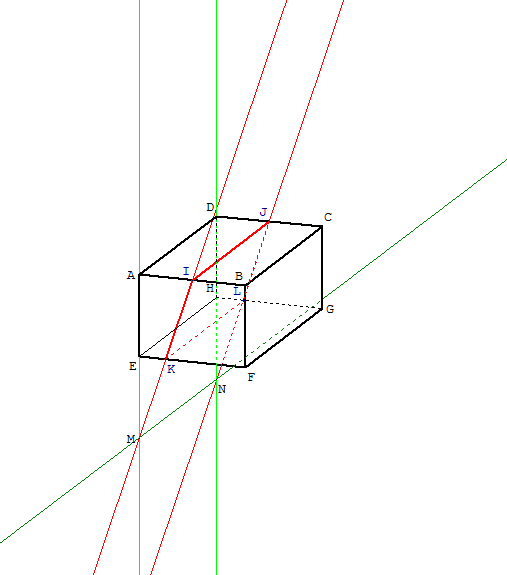
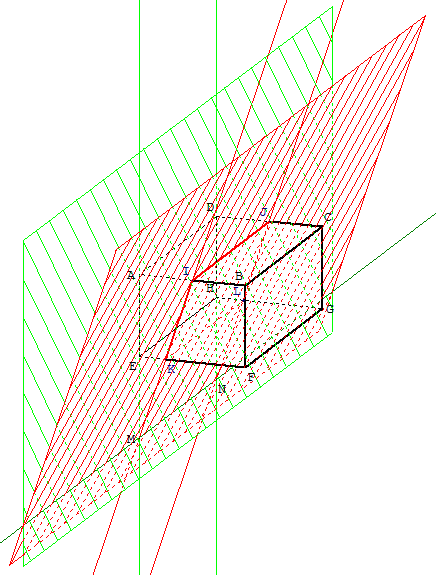
9. Intersection de deux plans
Section plane d'un parallélépipède
Ouvrir la figure GéoSpace parall.g3w
ABCDEFGH est un parallélépipède rectangle de côtés de longueurs a, b et h.
Avec GéoSpace
• Placer I le milieu de [AB] et J le milieu de [CD],
• Construire K un point du segment [EF] tel que EK = 
EF,
• Construire L un point du segment [GH] tel que HL = GH,
• Construire la droite (d), intersection des plans (IJK) et (ADE).
Un travail peut s'engager sur :
• justifier l'appartenance du point L au plan (IJK),
• justifier la construction,
• conjecturer ou utiliser le théorème du toit pour démontrer que (IJ) // (AD) // (MN).
Variantes
I et K sont deux points variables sur les côtés [AB] et [EF].
J est le point d'intersection du côté [CD] et de la parallèle à (AD) passant par I.
L est le point d'intersection du côté [GH] et de la parallèle à (EH) passant par K.
Si I est le milieu de [AB], montrer que J est le milieu [CD].
Si l'abscisse de K sur la droite repérée (E, F) est 1/4, montrer que l'abscisse de L sur la droite repérée (H, G) est 1/4.
Voir : sections planes d'un parallélépipède rectangle. En modifiant les longueurs a, b et h des côtés avec a = b = h, tracer un cube et examiner la section du cube par un plan parallèle à une arête.
Télécharger la figure GéoSpace parall_section.g3w
Télécharger la figure GéoSpace inter2p.g3w
Table des matières
Dans d'autres pages du site
Sections de cube en 3e
Sections de cube au lycée
Téléchargement
Télécharger activite_1s.doc :Google considère l'URL de ce document au format « .doc »
comme une erreur de type "soft 404".
Page no 34, réalisée le 26/2/2003
mise à jour le 4/2/2015