Descartes et les Mathématiques
Intersection inaccessible - Douze solutions
Construction d'une droite passant par un point et l'intersection de deux autres droites, sans utiliser cette intersection impossible.
Sommaire
Droite menée au point de concours
2. Deuxième figure de Desargues
3. Construction par polaires réciproques
4. Construction à la règle seule d'Ocagne
6. Parallélogramme de sommet M
Utilisation de droites remarquables d'un triangle
10. Quadrangle orthocentrique :
M orthocentre d'un triangle
M sommet d'un triangle d'orthocentre I
11. Bissectrices
Point inaccessible :
Angle de deux droites
Tracer le symétrique d'un triangle
Bissectrice
Perpendiculaire et carré avec règle et équerre
Diagonale d'un parallélogramme
Mobile friendly : Sur tablette ou smartphone, bascule automatique vers la version mobile
Droite passant par un point et par l'intersection inaccessible
Détermination de la droite passant par un point de la page et par l'intersection inaccessible
Deux droites concourantes se coupent en un point situé hors de la feuille (hors de l'écran). Par un point du plan, situé sur la feuille hors des droites, on demande de tracer la droite concourante, avec ces deux droites sans utiliser ce point inaccessible.
Vouloir réaliser ces constructions à la règle seule n'est pas un caprice de mathématicien. Le contexte militaire de la géométrie du XIXe siècle impose ces contraintes, lorsqu'il est trop dangereux de s'approcher de l'ennemi.
Il interdit aussi l'usage du compas, car il est impossible de réaliser des mesures sur le champ de bataille.
Point d'intersection hors de la feuille
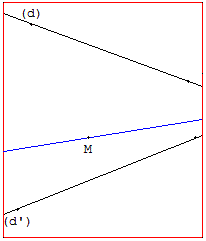
Compléter la feuille
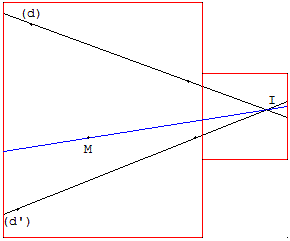
Point d'intersection hors de la feuille
Peut-on tracer la droite passant par M et par l'intersection de (d) et (d’) ?
Avec GéoPlan, il est possible de créer le point d'intersection I, hors de l'écran, et de tracer la droite (IM).
Télécharger la figure GéoPlan droites_concourantes.g2w
Compléter la feuille
Dans les conventions du problème, nous refusons
le collage d'un papier supplémentaire sur le bord de la page.
Télécharger la figure GéoPlan droites_concourantes2.g2w
Indications
Une situation à mettre en œuvre de la quatrième à la terminale, en deux à trois heures, suivant les niveaux et les objectifs.
Ce problème est classique et remonte sans doute à plusieurs siècles : ce qui est innovant est d'accepter plusieurs solutions sans aucun dogmatisme.
Ce problème est projectif et les solutions à la règle seule sont les plus élégantes.
Mais il peut aussi se résoudre dans un cadre affine avec translation et parallélogramme.
Un cadre euclidien est plus tiré par les cheveux, mais il est possible d'utiliser angles droits, orthocentre et bissectrices et pourquoi pas des pliages.
La grande supériorité de GéoPlan sur beaucoup de logiciels de géométrie est qu'il permet de concevoir des objets sans les visualiser.
Par contre avec Cabri, on devra faire des zooms arrière jusqu'à trouver le point inaccessible et revenir à la situation d'origine par des zooms avant.
Constructions à la règle
Deux droites (d) et (d’) concourantes se coupent en un point I situé hors de la feuille, M étant un point du plan, tracer la droite (IM).
1. Figure de Desargues
Ce problème de géométrie projective doit se traiter de préférence en utilisant la règle seule.
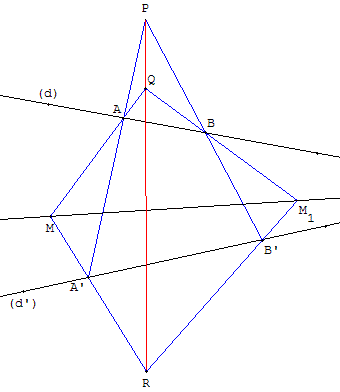
Tracer l'axe homologie (PQ) et trouver la droite (MM1)passant par le pôle I ;
Pour cela, effectuer les constructions suivantes en veillant à ce que les droites se coupent à l'intérieur de la feuille :
Placer deux points A et B sur (d), deux points A’ et B’ sur (d’) ; et un point Q sur la droite (AM).
Les droites (AA’) et (BB’) se coupent en P, la droite (MA’) coupe (PQ) en R.
Les droites (QB) et (RB’) se coupent en M1. La droite (MM1) passe par I.
Télécharger la figure GéoPlan droite_mi_desargues.g2w
Joindre un point avec l'intersection de 2 droites qui ne rentrent pas sur la feuille ?
Utilisation de l'espace pour un problème plan
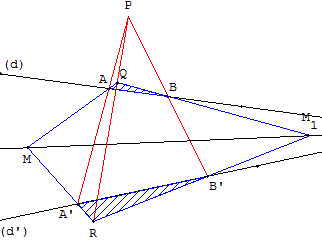
La démonstration « par le relief » est facile en imaginant les deux triangles QAB et RA’B’ comme la représentation de deux triangles de l'espace non situés dans le même plan. Le point P est alors le centre d'une perspective transformant QAB en RA’B’.
Les plans (QAB) et (RA’B’) se coupent suivant une droite (d), qui s'appelle l'axe d'homologie. Les droites (QA) et (RA’) se coupent en un point M qui est donc situé sur (d). De même, les points M1 et I sont situés sur (d). La droite (MM1), droite d'intersection des deux plans, passe par I.
Remarque : dans cette démonstration on utilise le fait que deux droites de l'espace projectif se coupent que si elles sont coplanaires, le point d'intersection étant un point à l'infini lorsque les deux droites sont parallèles. Le point M existe, car les droites (QA) et (RA’) sont situés dans le plan (PAQ). Les points M1 et I existent également.
Figure reprise dans : joindre deux points d'une droite avec une règle trop courte
2. Deuxième figure de Desargues
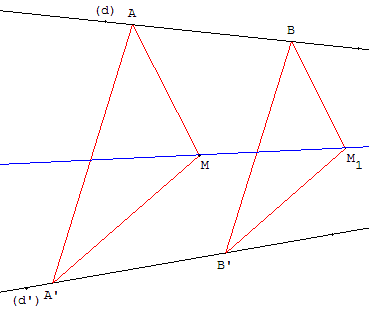
Cas où les droites (AA’) et (BB’) sont parallèles.
Dans le plan projectif, la droite (PQ) est alors la droite de l'infini.
Placer deux points A et B sur (d) et un point A’ sur (d’).
La parallèle à (AA’) passant par B coupe (d’) en B’.
Les parallèles à (AM) et (A’M) passant par B et B’ se coupent en M1.
La droite (MM1), qui passe par I, est solution.
Remarques : cette solution utilise la forme affine du théorème de Desargues. Elle correspond au cas de la première figure de Desargues, où la droite (PQ) est rejetée à l'infini.
On utilise le triangle AA’M1, semblable au triangle AA’M, image par une homothétie de centre I transformant une sécante (AA’) à (d) et (d’) en une sécante (BB’) parallèle.
La construction est toujours possible et peut être réalisée avec une équerre ou avec la règle à bords parallèles.
Télécharger la figure GéoPlan droite_m_pt_concours.g2w
3. Construction à la règle seule, par polaires réciproques
D'après Jean-Henri Lambert (1728-1777)
Solution historique, maintenant hors programme, avec des faisceaux harmoniques de droites pour ma génération de retraités nostalgiques.
Les origines de cette construction se trouvent dans la préoccupation des peintres de tracer des parallèles en perspective sans sortir du tableau.
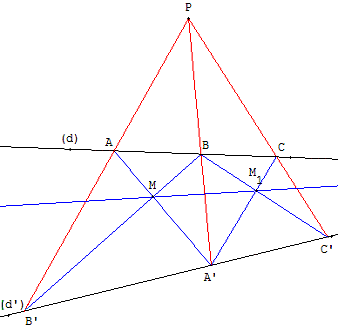
M entre (d) et (d’ )
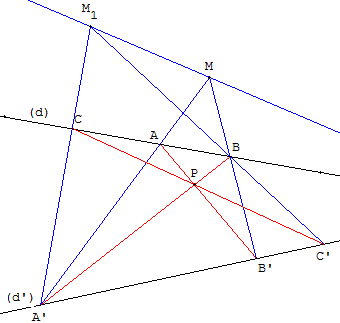
M à l'extérieur de (d) et (d’)
Télécharger la figure GéoPlan droite_mi_polaire.g2w,
Construire un point P de la polaire de M par rapport à (d) et (d’) :
Placer deux points A et B sur (d). La droite (MA) coupe (d’) en A’ et la droite (MB) coupe (d’) en B’.
Le point P intersection de (AB’) et (A’B) est un point de la polaire de M.
Construire la polaire de P par rapport à (d) et (d’) :
Placer un point C, distinct de A et B, sur (d). La droite (MC) coupe (d’) en C’.
Le point M1 intersection de (A’C) et (BC’) est un point de la polaire de P.
La droite (MM1), polaire de P, passe par I.
Voir, pour des droites parallèles (d) et (d’ ), la construction de la parallèle à (d) passant par M.
4. Construction à la règle seule d'Ocagne
Placer deux points A et B sur (d), deux points A’ et B’ sur (d’).
Les droites (MA) et (BB’) se coupent en C, les droites (MB’) et (AA’) se coupent en C’.
Les droites (BC’) et (A’C) se coupent en M1. La droite (MM1) passe par I.
Télécharger la figure GéoPlan droite_mi_ocagne.g2w
Un cercle (c) coupe la droite (d) aux points A et B, la droite (d’) aux points A’ et B’.
La droite (MA) recoupe le cercle en C, la droite (MB’) recoupe le cercle en C’.
5. Avec un cercle auxiliaire - Droite de Pascal
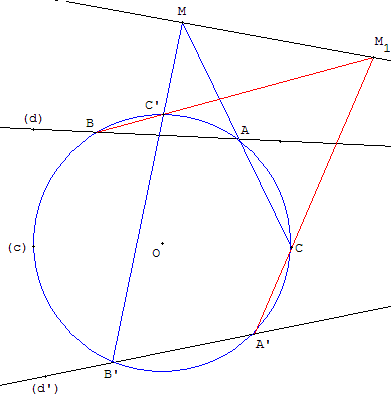
Les droites (BC’) et (A’C) se coupent en M1. La droite (MM1) passe par I.
Remarque : ce résultat est une conséquence du théorème de Pascal ; le point I est aligné avec les points M et M1 sur la droite de Pascal (MM1) de l'hexagramme ABC’B’A’C.
Télécharger la figure GéoPlan droite_mi_cercle.g2w
Pliage
Construction par pliage de la droite passant par un point M et par l'intersection inaccessible de deux droites (d) et (d’)
Les pliages permettent de résoudre le problème dans le cas où M est entre (d) et (d’) :
Amener (d) en coïncidence avec (d’), la trace du pli donne la bissectrice (d3).
Si M est entre (d) et (d3) on recommence en amenant (d) sur (d3) pour obtenir un pli (d4), sinon amener (d’) sur (d3), et ainsi de suite en rabattant l'une sur l'autre les deux droites entre lesquelles le point M est situé…
Au bout de 5 ou 6 pliages maxima, la position de la droite (IM) sera connue au millimètre près.
Géométrie affine : parallélogrammes ou homothétie
6. Parallélogramme inaccessible de sommet M
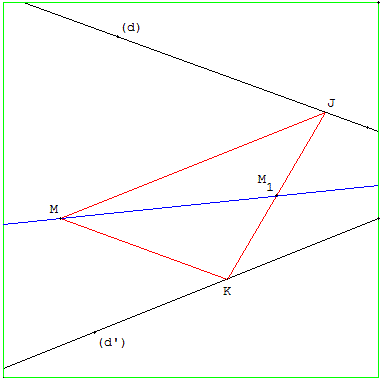
Tracer la droite (MI) cherchée comme diagonale d'un parallélogramme IJMK dont les côtés sont portés par (d) et (d’).
Construction
Tracer les parallèles à (d) et (d’) qui passent par M.
La parallèle à (d) coupe (d’) en K ; la parallèle à (d’) coupe (d) en J.
IJMK est un parallélogramme.
Rechercher le milieu M1 de la diagonale [JK].
La solution est la droite (MM1) passant par M et par le milieu M1 de [JK], deuxième diagonale du parallélogramme.
La construction est possible si les points J et K sont situés dans la feuille.
Télécharger la figure GéoPlan para_sommet_M.g2w
Voir : diagonale d'un parallélogramme sur une feuille trop petite
7. Parallélogramme inaccessible de centre M
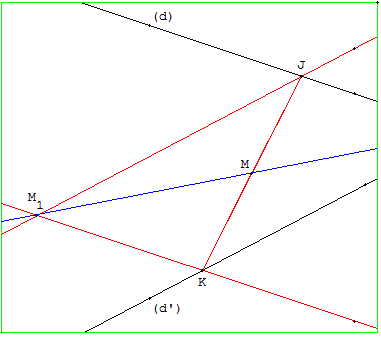
Une variante peut être de tracer la droite (MI) cherchée comme diagonale d'un parallélogramme IJM1K de centre M dont les côtés sont portés par (d) et (d’).
Construction
Pour cela, il suffit de construire les droites symétriques de (d) et (d’) par rapport à M.
L'intersection M1 de ces deux nouvelles droites (si elle existe sur la page) fournit un troisième point de la droite cherchée.
On obtient un parallélogramme IJM1K dont la diagonale (M1M) est la droite cherchée.
La construction est possible si les points J, K et M1 sont situés dans la feuille.
Télécharger la figure GéoPlan para_centre_M.g2w
8. Homothétie de rapport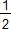 
8.a. Utiliser une homothétie de centre M transformant (d) et (d’) pour obtenir un troisième point M1 de la droite cherchée.
Construction
Tracer la perpendiculaire à (d) qui passe par M, elle coupe (d) en J.
Tracer la perpendiculaire à (d’) qui passe par M, elle coupe (d’) en K.
Tracer la parallèle à (d) qui passe par le milieu de [MJ].
Tracer la parallèle à (d’) qui passe par le milieu de [MK].
Ce sont les images de (d) et (d’) par l'homothétie de centre M et rapport .
Ces deux parallèles se coupent en M1, image de l'intersection I par l'homothétie.
Le centre M, le point I et son image M1 sont alignés.
La droite (MM1) passe par I et est solution.
Télécharger la figure GéoPlan homothetie.g2w
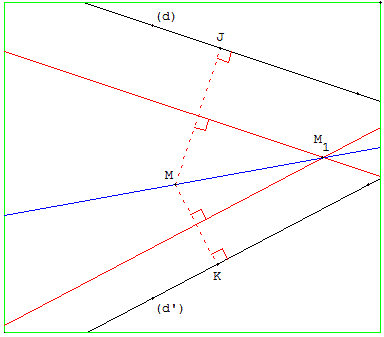
8.b. Utiliser une homothétie de centre O, situé sur (d’), transformant (d) pour obtenir une droite parallèle à la droite cherchée.
Construction
Tracer la perpendiculaire à (d) qui passe par M, elle coupe (d) en H et (d’) en O.
Soit M’ le milieu de [OM] et H’ le milieu de [OH]. M’ et H’ sont les images de M et H par l'homothétie de centre O et de rapport .
L'image de (d) est la parallèle à (d) passant par H’. Elle coupe (d’) en I’, image de I par l'homothétie.
La parallèle passant par M à la droite (M’I’) est son image réciproque. Elle passe par I.
Télécharger la figure GéoPlan homothetie2.g2w
Et si l'homothétie de rapport ne suffit pas, on peut utiliser une homothétie de rapport 
, 
, 
… pour placer le point M1 ou le point I’ dans la feuille.
9. Translation et parallélogramme
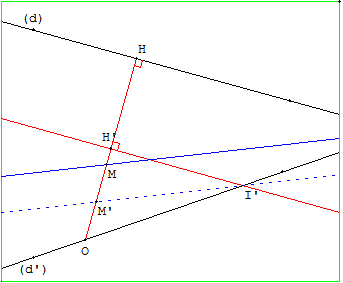
Le point I étant hors de l'écran, tracer la droite (MI) cherchée comme quatrième côté d'un parallélogramme I’M’MI.
Construction
Du côté de I, notons (D) le bord de la feuille (ou si M est avant le deuxième tiers de la feuille, une parallèle au bord plus près de M),
– soit (D’) la parallèle à (D) passant par M,
– le point A est la projection orthogonale de M sur (D),
– B et C sont les intersections de (D) avec les droites ((d) et (d’),
– I1 est le point d'intersection des droites symétriques de (d) et (d’), par rapport aux perpendiculaires à (D) en B et C.
– I’ le symétrique de I1 par rapport à (D’),
– M’ est l'image de M par la translation de vecteur 2 
,
– pour tracer la droite (MI) solution, il suffit donc de mener, par le point M, la parallèle à la droite (I’M’).
Indications : symétries et translation
Soit I1 le symétrique de I par rapport à (D). On peut tracer I1 en remarquant que les droites (d1) et (d2), symétriques de (d) et (d’) par rapport à D, se coupent en I1.
À l'intérieur de la feuille, pour tracer la droite (d1), symétrique de (d), noter que cette droite passe par le point B intersection de (D) et (d), et utiliser le fait que (d1) est aussi symétrique de (d) par rapport à la perpendiculaire à (D) en B.
De même (d2), symétrique de (d’), est symétrique de (d’) par rapport à la perpendiculaire à (D) en C.
Soit I’ le symétrique de I1 par rapport à (D’).
Le point I’ est l'image de I par la composée des symétries par rapport à
(D) et (D’),
I’ est donc l'image de I par la translation de vecteur 2 .
Parallélogramme
L'image M par cette translation de vecteur 2 est M’: II’M’M est alors un parallélogramme tel que 
= 
= 2 .
Pour tracer (IM) il suffit donc de mener, par le point M, la parallèle à la droite (I’M’).
Télécharger la figure GéoPlan para_translation.g2w
Utilisation de droites remarquables d'un triangle
10. Quadrangle orthocentrique
10.a. Orthocentre d'un triangle inaccessible
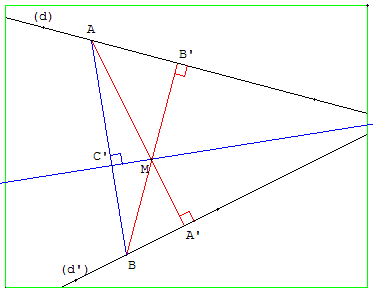
M orthocentre d'un triangle inaccessible ABI
Tracer la droite (MI) cherchée comme troisième hauteur (C’M) d'un triangle MAB ayant pour orthocentre I.
Construction
Tracer la perpendiculaire à (d’) passant par M, coupant (d) en A et coupant (d’) en A’.
Tracer la perpendiculaire à (d) passant par M, coupant (d’) en B et coupant (d) en B’.
(MA) et (MB) sont deux hauteurs du triangle ABI et M est l'orthocentre de ce triangle.
La droite (MI), troisième hauteur de ce triangle, est perpendiculaire au côté (AB).
Tracer la perpendiculaire issue de M à (AB) qui est la solution du problème.
MABI est un quadrangle orthocentrique : I est l'orthocentre de MAB.
Télécharger la figure GéoPlan droite_mi_ortho2.g2w
10.b M Sommet d'un triangle d'orthocentre le point inaccessible
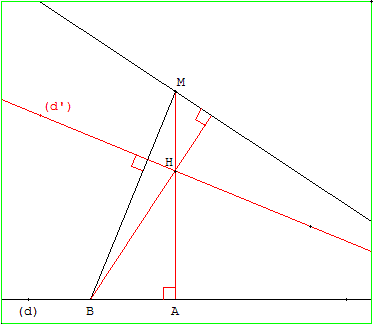
Classe de première L
Trouver un triangle MBH, de sommet M tel le point inaccessible I, soit l'orthocentre de ce triangle. (d) et (d’)sont deux hauteurs du triangle, la droite cherchée (MI) est la troisième hauteur du triangle, perpendiculaire issue de de M à (BH.)
Construction
Tracer la perpendiculaire à (d) passant par M la coupant en A et coupant (d’) en H.
Tracer la perpendiculaire à (d’) passant par M qui coupe (d) en B.
Le point H est l'orthocentre du triangle MBI.
La droite cherchée est perpendiculaire issue de M à la hauteur (BH) : le côté (MI) du triangle.
MBIH est un quadrangle orthocentrique : I est l'orthocentre de MBH.
Télécharger la figure GéoPlan droite_mi_ortho.g2w
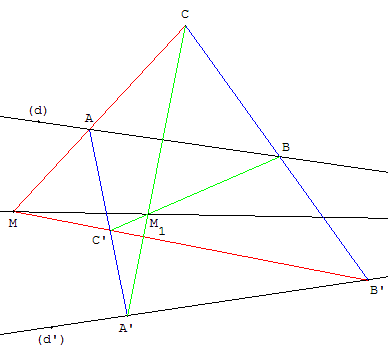
11. Bissectrice et centre d'un cercle inscrit
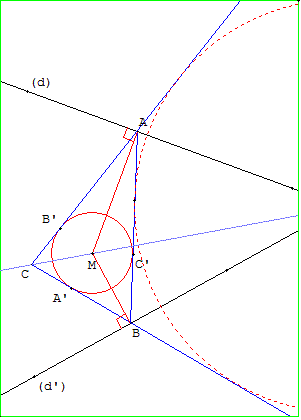
Construction d'une bissectrice déterminée le troisième sommet C d'un triangle ABC ayant deux sommets A et B sur l'angle et par le centre M du cercle inscrit.
La droite (CM), bissectrice de ACB, est la droite cherchée. Elle passe par le sommet inaccessible I, de l'angle, qui est le centre d'un cercle exinscrit au triangle ABC.
En général, on peut aussi considérer un triangle ABC avec A sur (d), B sur (d’) et tel que (d) et (d’) soient deux bissectrices intérieures ou extérieures du triangle ABC. Alors la droite cherchée sera la bissectrice de l'angle ACB, passant par M, centre du cercle inscrit ou exinscrits au triangle ABC.
Construction
Soit A et B les projections orthogonales de M sur (d) et (d’).
Construire le point C tel que (AM) et (BM) soient des bissectrices du triangle ABC.
Pour cela, soit C’ la projection orthogonale de M sur (AB) et (c) le cercle de centre M passant par C’.
Si M est entre les droites (d) et (d’), (c) est inscrit dans le triangle ABC.
Si M est à l'extérieur des droites (d) et (d’), le cercle (c) est exinscrit dans l'angle ACB.
Soit B’ et A’ les symétriques de C’ par rapport à (AM) et (BM). Les droites (AB’) et (BA’), tangentes au cercle (c), sont les côtés du triangle. Leur point d'intersection est le sommet C.
La droite (CM) est bissectrice de ACB.
Elle est concourante en I avec les deux autres bissectrices (d) et (d’).
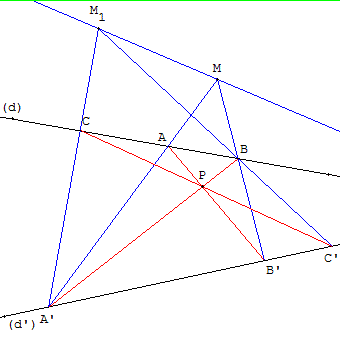
Dans le cas de la figure ci-dessus, M et I sont situés sur une bissectrice intérieure. I est le centre du cercle exinscrit dans l'angle ACB.
Dans la figure ci-contre, M est à l'extérieur de l'angle des droites (d) et (d’), M et I sont situés sur une bissectrice extérieure à ACB. Ce sont les centres de deux cercles exinscrits au triangle ABC.
Télécharger les figures GéoPlan droite_mi_bissect.g2w,
Voir une douzième solution : tracé par pliage (répétition de la technique de la bissectrice)
Table des matières
Voir : point inaccessible
Lien
En collaboration avec unininge
Faire des mathématiques en co-enseignement : une aide pour penser les mathématiques
Vers des situations complexes mobilisant d'autres postures
Proposer une situation complexe dans l'idée de prolonger le travail mené dans les phases de structuration-systématisation, dans le passage de l'école au collège. C'est le cas du problème de Lambert. On se donne deux droites qui se coupent en dehors d'un cadre, un point dans ce cadre. Il s'agit de proposer une méthode pour tracer le segment de droite qui passe par ce point et l'intersection des deux droites. Cette situation visant à provoquer des propositions des élèves, du débat pour tenter de convaincre. Elle s'inscrit, à l'inverse des situations précédentes, sur un temps long.
L'institutionnalisation peut comporter plusieurs volets (Quelles postures du chercheur face à un problème “ouvert” ? La possibilité d'obtenir différentes méthodes de résolution et en particuliers parmi elles, la solution proposée par Lambert (Résolution à la fois “simple” et “mystérieuse” car utilisant huit fois la règle non graduée et des concepts de perspective). Pour visiter différentes méthodes on peut consulter cette page.
Page no 102, créée le 18/1/2007
modifiée le 12/4/2009