Descartes et les Mathématiques
Le triangle au collège
Milieux et parallèles
Six exercices de géométrie plane avec un logiciel de géométrie dynamique - Construction de triangles.
Sommaire
2. Somme des angles d'un triangle
4. Construction de deux triangles rectangles autour de BOA
Sur tablette numérique ou smartphone,
bascule automatique vers la version mobile
Dans d'autres pages du site
Triangles en seconde
Triangle
Définition
Un triangle est une figure plane, formée par trois points appelés sommets. Les côtés sont les segments qui joignent les sommets deux à deux.
Triangle plat
Un triangle plat est un triangle dégénéré dont les sommets sont alignés.
Par la suite, nous considérons des triangles non plats.
1. Triangles particuliers
Classe de sixième (sauf Thalès et Pythagore pour le triangle rectangle en troisième)
Triangle isocèle
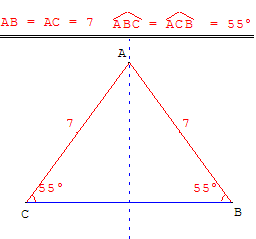
Un triangle isocèle a deux côtés de même longueur. Le troisième côté s'appelle la base.
Thalès a découvert que dans un triangle isocèle les angles à la base sont égaux.
La médiatrice de la base est axe de symétrie du triangle.
Figure interactive dans GeoGebraTube : triangle isocèle
Triangle équilatéral
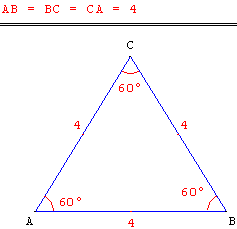
Un triangle équilatéral a ses trois côtés de même longueur, les trois angles sont égaux et mesurent 60 degrés.
Les trois médiatrices sont axes de symétrie du triangle.
Figure interactive dans GeoGebraTube : triangle équilatéral
Triangle rectangle
Un triangle rectangle a un angle droit, les deux autres angles sont aigus et complémentaires.
Le plus grand côté est l'hypoténuse : c'est le côté opposé à l'angle droit.
Un côté adjacent à l'angle droit est appelé cathète.
Thalès : un triangle rectangle s'inscrit dans un demi-cercle et réciproquement.
Pythagore : la somme des carrés des longueurs des côtés de l'angle droit est égale au carré de la longueur de l'hypoténuse et réciproquement.
Télécharger la figure GéoPlan tri_rect.g2w
Triangle quelconque
Par nature, un triangle est quelconque.
Un triangle est dit « triangle quelconque » s'il n'est ni rectangle, ni isocèle (ce qui exclut également le cas équilatéral).
Un triangle peut posséder ou non des propriétés de triangles particuliers. Si on précise triangle quelconque, on se place dans un cas général où on peut penser qu'il n'est pas plat, que les côtés sont inégaux et qu'il n'y a pas d'angle droit. Ceci n'exclut pas les cas particuliers où, par abus de langage, le triangle quelconque serait plat, ou rectangle, ou isocèle, ou encore équilatéral.
Au début d'un exercice, on peut écrire :
— Soit un triangle ABC quelconque ...
Ce qui n'empêche pas de trouver en conclusion un triangle particulier.
Par contre le professeur qui noterait :
— Soit un triangle quelconque ABC équilatéral ...
serait certainement franchement chahuté !
Triangle scalène
Un triangle qui n'est pas isocèle est dit « scalène » Un triangle scalène peut aussi être rectangle.
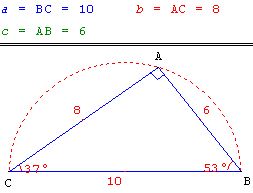
Variables dans un triangle
Mesures dans un triangle
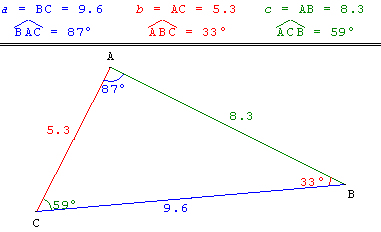
Télécharger la figure GéoPlan tri_quel.g2w, tri_quel2.g2w
Arrondi
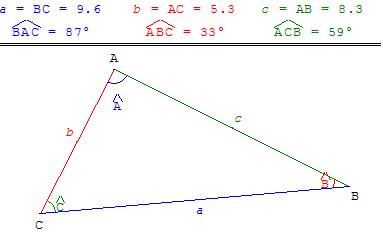
Avec les angles BAC = 87°, ABC = 33°, ACB = 59°, la somme de ces angles est égale à 179°. Plus bas vous dites que la somme des angles d'un triangle est égale à 180°.
Les mathématiques étant maintenant loin derrière pour moi, et étant un brin fatigué au moment où je vous écris ce mail, il subsiste encore un doute, mais je pense qu'un degré s'est perdu en route.
S'il s'agissait d'un centime, nous n'aurions pas chipoté, mais là il s'agit de mathématiques.
MonsieurPommeDeTerre
Pas d'erreur, mais un souci d'arrondi : les calculs étant faits « au degré près », GéoPlan arrondi les trois angles par défaut et on perd un degré pour l'arrondi de la somme.
Avec un calcul au dixième les angles BAC = 87,5°, ABC = 33,5° sont arrondis par excès et ACB = 59,0° par défaut : la somme est bien arrondie à 180,0°.
Technique GéoPlan
Pour nommer a un côté comme [BC], placer un point comme A8 milieu de [BC], et écrire à la fin du texte de la figure l'instruction :
A la place de A8, afficher: $ia
(pour italique avec $i, voir formatage d'un texte).
Ou bien avec la valeur de a, la longueur de BC :
Ou avec le menu créer> numérique>calcul géométrique >longueur d'un segment, nommer a la longueur de BC ; puis l'instruction :
A la place de A8, afficher: \val(a,1)\
Instruction qui affiche la longueur le long du segment.
La commande affichage du texte : $ia$m = BC = val(a,1) permet d'écrire a = BC = 9.6.
Le prototype marquer un angle trace un arc de cercle dans le coin d'un angle (dans le sens trigonométrique).
Le prototype point dans angle renvoie un point de la bissectrice dans le coin de l'angle.
Associé à l'instruction A la place de … afficher : \hat… \ il permet de nommer les angles 
, 
, 
.
A9 point dans angle BAC A la place de A9, afficher: \hat(A)\
Avec a’ mesure de l'angle 
, la commande affichage du texte : \hat(BAC)\ = val(a',0)° permet d'écrire = 87°.
Remplacer val(a',0) par val(a',1), pour écrire = 87.5° avec une décimale.
Périmètre du triangle
Somme des côtés d'un triangle :
Le périmètre d'un triangle est égal à la somme des longueurs des côtés du triangle.
Le périmètre du triangle ABC est p = AB + BC + CA.
2. Somme des angles d'un triangle
Classe de cinquième
La somme des angles géométriques d'un triangle est un angle plat : + + = 180°.
Pour un triangle isocèle en A, = donc = 180 - 2 et = = 90 - 
: les angles égaux sont aigus.
Pour un triangle équilatéral = = = 
= 60°.
Un triangle a au moins deux angles aigus. Si le troisième angle est :
• droit, on parle de triangle rectangle : pour un triangle rectangle en A, = 90°, + = 90° : les deux angles aigus sont complémentaires.
• obtus, on parle de triangle obtusangle : un triangle admet au maximum un angle obtus : si > 90°, + < 90°, les deux autres angles sont aigus.
• aigu, on parle de triangle acutangle : les trois angles sont aigus.
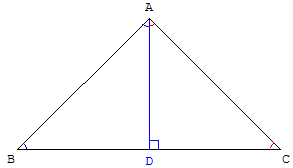
2.a. Démonstration des « anciens Grecs »
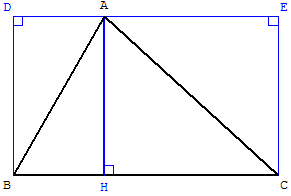
Le résultat donnant la somme des angles d'un triangle est connu des anciens. Il aurait été découvert par Thalès et les disciples de Pythagore auraient rédigé une démonstration.
ABC est un triangle et [AH] une hauteur (si le triangle est obtusangle, on choisira la hauteur issue du sommet de l'angle obtus, [BC] étant alors le plus grand côté).
On peut inscrire le triangle dans un rectangle BCED.
Dans le rectangle BHAD, les angles BAH et ABD sont de même mesure (angles alternes internes par rapport à la diagonale [AB] et les côtés parallèles [AH] et [BD]).
De même HAC = ECA.
La somme des angles du triangle ABC + BAC + ACB = ABC + BAH + HAC+ ACB.
Avec les angles alternes internes, on trouve que cette somme est
ABC + ABD + ECA+ ACB = CBD + ECB, soit 2 angles droits ou 180°.
Télécharger la figure GéoPlan triangle_ds_rectangle.g2w
2.b. Figure des disciples de Pythagore
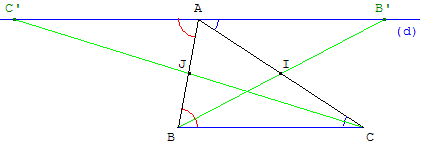
Vers le Ve siècle avant J.-C.
On mène par A une parallèle (d) à (BC).
La somme des angles du triangle est égale à l'angle plat en A.
Télécharger la figure GéoPlan somme_angles.g2w
Démonstration des pythagoriciens
La symétrie centrale, et la caractérisation angulaire du parallélisme qui en découle, permet de démontrer que la somme des angles d'un triangle est égale à 180 degrés.
2.b. On mobilise deux fois le même pas de démonstration, qui consiste à utiliser les symétries centrales de centre I et J milieux de [AC] et de [AB], transformant la droite (BC) en (d), pour établir les égalités d'angles CBA = C’ÂB et ACB = CÂB’
et on conclut avec l'angle plat C’ÂB’ = C’AB + BÂC + CÂB’ = CBA + BÂC + ACB = + + = 180°.
2.c. Dans la figure d'Euclide ci-dessous, en traçant la parallèle au troisième côté, on montre que l'angle extérieur est égal à la somme de deux angles, pour les angles correspondants et pour les angles alternes-internes.
2.d. Pliage d'un triangle selon une droite des milieux, voir : construction par pliage
2.c. Figure d'Euclide
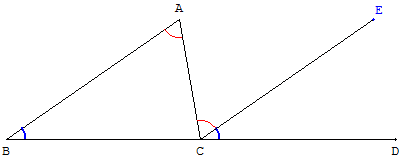
L'angle extérieur d'un triangle est égal à la somme des deux angles intérieurs non adjacents.
Télécharger la figure GéoPlan angle_exterieur.g2w
Calcul avec des angles orientés
Classe de seconde
La somme des angles orientés (
, 
) + (
, 
) + (
, 
) est un angle plat.
En effet, par translation de vecteur on a :
(, ) = (
, 
)
et par symétrie de centre le milieu de [AC] :
(, ) = (, ).
D'où la relation de Chasles :
(, ) + (, ) + (, ) = (, ).
Les éléments d'Euclide - Livre I - Proposition 32
IIIe siècle avant J.-C.
Blaise Pascal
Étienne Pascal décréta que son fils n'apprendrait pas les mathématiques avant l'âge de 15 ans, et fit disparaître les livres de mathématiques de sa maison. Cependant Blaise commença à travailler seul en géométrie à l'âge de 12 ans. Il découvrit que la somme des angles d'un triangle valait deux angles droits et, quand son père le découvrit, il se ravisa et lui permit de lire les Éléments d'Euclide.
3. Droite des milieux
Classe de quatrième
Premier théorème des milieux
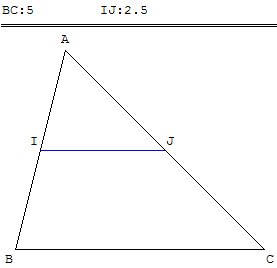
Théorème direct de la droite des milieux
Si une droite passe par les milieux de deux côtés d'un triangle alors elle est parallèle au troisième côté.
Dans un triangle ABC, si I est le milieu de [AB] et J le milieu [AC], alors (IJ) est parallèle à (BC).
Deuxième théorème des milieux
Théorème réciproque
Si une droite parallèle à un côté d'un triangle passe par le milieu d'un autre côté alors elle passe par le milieu du troisième côté.
Dans un triangle ABC, soit I le milieu de [AB]. La parallèle à (BC) passant par I coupe (AC) en J.
J est alors le milieu [AC].
Troisième théorème des milieux
Dans un triangle ABC, si I est le milieu de [AB] et J le milieu [AC], alors IJ = 
BC.
Théorème direct
Formulation des deux énoncés du théorème direct :
Si un segment a pour extrémités les milieux de deux côtés d'un triangle, alors il est parallèle au troisième côté, et sa longueur est égale à la moitié de celle du troisième côté.
Démonstration du théorème de la droite des milieux
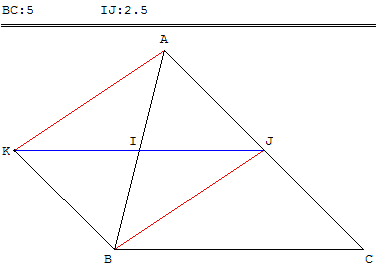
Création d'un point auxiliaire K qui fait apparaître deux parallélogrammes : KBJA et KBCJ.
Soit I le milieu de [AB] et J le milieu [AC]. Tracer le symétrique K de J par rapport à I. I est alors le milieu de [KJ] et IJ = KJ.
Comme par hypothèse I est le milieu de [AB], les diagonales de KBJA se coupent en leur milieu commun I, donc KBJA est un parallélogramme.
Les côtés [AJ] et [KB] sont parallèles et de même longueur, et il en est donc de même pour [JC] et [KB],
donc KBCJ, quadrilatère non croisé, est aussi un parallélogramme.
Par les propriétés de ce parallélogramme, les côtés opposés [KJ] et [BC] sont parallèles, la droite (IJ) est donc parallèle à (BC) ce qui prouve le premier théorème des milieux.
On sait que IJ = KJ. Comme les côtés opposés du parallélogramme sont égaux, de KJ = BC on déduit le troisième théorème des milieux :
IJ = BC.
Démonstration du deuxième théorème des milieux
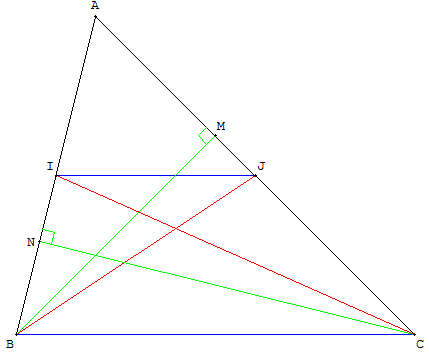
Le deuxième théorème des milieux est la réciproque du premier et est un cas particulier du théorème direct de Thalès : l'unicité de la parallèle à (BC) passant par I, on en déduit que la droite des milieux est confondue avec cette parallèle : elle coupe (AC) au milieu J de [AC].
Autre démonstration par la méthode des aires
En effet, Aire(ABC) = Aire(IBC) + Aire(IAC).Or IA = IB, donc Aire(IBC) = Aire(IAC) =
(CN × IB) où CN est la hauteur du triangle ABC issue de C.Méthode des aires : démonstration utilisant la propriété d'Euclide :
« les triangles qui ont la même hauteur sont l'un relativement à l'autre comme leurs bases ».
Montrer que AJ = JC.
D'après la propriété du trapèze, les triangles IBC et JBC ont la même aire.
Cette aire est égale à la moitié de l'aire du triangle ABC.
Donc, l'aire du triangle ABJ (complément dans ABC du triangle CBJ) est aussi égale à la moitié de celle de ABC et donc égale à l'aire du triangle CBJ.
En revenant à l'expression de l'aire d'un triangle, comme les deux triangles ABJ et CBJ ont la hauteur BM, issue de B, en commun,
Aire(ABJ) = (BM × AJ) est égal à Aire(CBJ) = (BM × JC).
Les longueurs AJ et JC sont alors égales et J est le milieu de [AC].
Télécharger la figure GéoPlan milieux.g2w
WikiPédia : Théorème des milieux
4. Construction de deux triangles rectangles
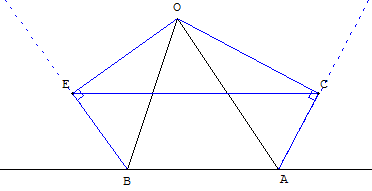
Construction à l'extérieur d'un triangle BOA.
À l'extérieur d'un triangle BOA on construit deux triangles rectangles :
– Le triangle OAC, ayant pour hypoténuse le côté [OA], tel que le sommet C de l'angle droit soit situé sur la bissectrice extérieure de OAB.
– Le triangle OBE, ayant pour hypoténuse le côté [OB], tel que le sommet E de l'angle droit soit situé sur la bissectrice extérieure de OBA.
Que dire de [EC] ?
Figure
Les triangles rectangles OAC et OBE sont inscrits dans les cercles de diamètres [OA] et [OB].
Le deuxième point I d'intersection de ces cercles est le pied de la hauteur de BOA, issue de O.
Commande GéoPlan
Taper S pour la Solution
Télécharger la figure GéoPlan tr_boa.g2w
Indications : triangles rectangles extérieurs à BOA
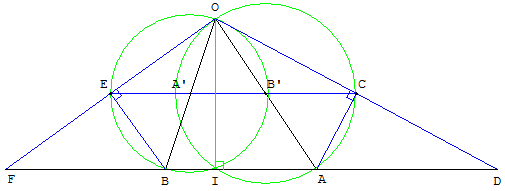
Prolonger (OC) et (OE), en D et F, jusqu'à la droite (AB).
[AC] est la hauteur et la bissectrice issue de A du triangle OAD. Les angles DAC et CAO des triangles rectangles CDA et COA sont de même mesure.
Les deux autres angles aigus CDA et COA sont égaux : OAD est isocèle.
De même le triangle OBF est isocèle.
D'où DF = DA + AB + BF = OA + AB + BO est égal au périmètre du triangle OAB.
(EC) est une droite des milieux du triangle ODF et contient les milieux A’ et B’ de [OB] et [OA].
Elle est parallèle à (AB) et [EC] est de longueur égale à la moitié du périmètre DF du triangle OAB.
Autre calcul : avec CE = CB’ + B’A’ + A’E, les rayons des cercles sont :
CB’ = OA et A’E = OB.
(B’A’) est une droite des milieux du triangle BOA, d'où B’A’ = AB.
CE = (OA + OB + AB) est bien égal à la moitié du périmètre de BOA.
Autre figure : voir diamètres de deux cercles sécants
5. Angles et triangles
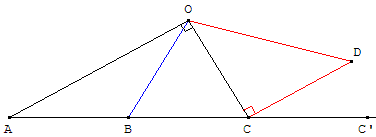
OBC est un triangle équilatéral.
OAC est un triangle rectangle (B milieu de l'hypoténuse).
OCD est un triangle rectangle isocèle en C.
Trouver les mesures des angles de cette figure.
Télécharger la figure GéoPlan triang_1.g2w
6. Triangle rectangle isocèle
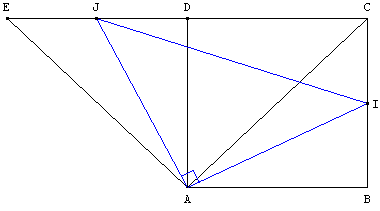
ABCD est un carré.
E est le symétrique de C par rapport à D.
I est le milieu de [BC], J est le milieu de [DE].
Montrer que le triangle AIJ est rectangle isocèle en A.
Télécharger la figure GéoPlan triang_2.g2w
7. Deux droites parallèles
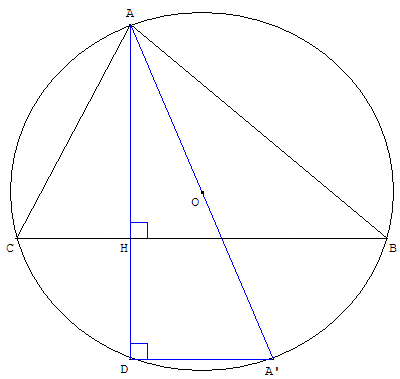
Soit ABC un triangle et son cercle circonscrit (c) de centre O.
A’ est le point diamétralement opposé à A sur le cercle (c).
La hauteur (AH) issue de A du triangle ABC recoupe le cercle (c) au point D.
Montrer que la droite (DA’) est parallèle à (BC).
Indication
Le triangle rectangle ADA’ est inscrit dans un demi-cercle.
Télécharger la figure GéoPlan dr_para.g2w
8. Trouver un triangle isocèle
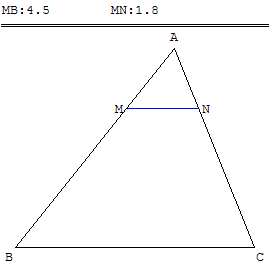
Classe de quatrième, troisième ou seconde
ABC est un triangle,
M un point du segment [AB],
la parallèle à (BC) passant par M coupe [AC] en N.
Où doit-on placer le point M pour que le triangle BMN soit isocèle en M ?
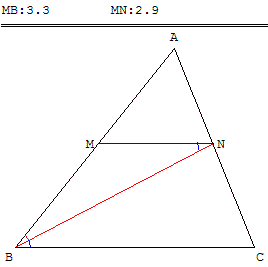
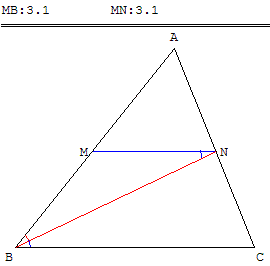
Le point N est sur la bissectrice de l'angle ABC.
Télécharger la figure GéoPlan ch_t_iso.g2w
9.a. Triangle bisocèle
Un triangle bisocèle est un triangle isocèle qui est partagé, par l'une de ses bissectrices, en deux triangles eux-mêmes isocèles.
Triangle isocèle rectangle
Ce découpage de ABC en deux triangles isocèles est le seul cas où les angles aux sommets (aigus au sens large) sont adjacents sur un même côté du triangle ABC.
Télécharger la figure GéoPlan rect_iso.g2w
Trouver un autre triangle bisocèle
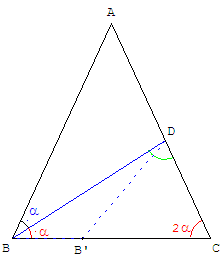
Un raisonnement simple sur les angles, par exemple l'angle A, nous permet une recherche avec un logiciel de géométrie dynamique.
Dans un triangle isocèle ABC, de base [BC], si une sécante (BD) le partage en deux triangles isocèles, un des triangles aura pour base [AB], l'autre pour base [CD].
Si D est le point d'intersection de la médiatrice de [AB] avec [AC],
ABD est un triangle isocèle d'angles α = BÂC = ABD. Le supplément de l'angle au sommet est BDC = 2α.
La médiatrice de [CD] coupe (BC) en B’.
Il est possible de faire une recherche en déplaçant le point A, afin que le point B’ coïncide avec le sommet B.
Télécharger la figure GéoPlan bisocele.g2w
Triangle d'or
Solution pour α = 36°
Le triangle d'or comme solution :
ABC et BCD sont des triangles d'or d'angles 36° et 72°.
ABD est un triangle d'argent d'angles 108 ° et 36°.
Télécharger la figure GéoPlan trian_or.g2w
Indications
Soit ABC un triangle isocèle de base [BC] et d'angle à la base ABC = 2α (α > 0) et une bissectrice qui coupe le côté opposé en D.
Si la bissectrice est issue du sommet A, c'est aussi la médiatrice et (AD) partage le triangle ABC en deux triangles rectangles isocèles ADB et ADC. Les angles aigus sont de 45°. L'angle en A est de 90° et le triangle ABC est rectangle isocèle.
Si la bissectrice (AD) est issue d'un des sommets de la base, B par exemple, le triangle BDC doit être isocèle. L'angle BDC est alors égal à α ou à 2α.
α est une valeur impossible :
en effet, les droites (AD) et (AB) déterminant deux angles alternes-internes égaux à α par rapport (BD) seraient parallèles, ce qui est contradictoire avec l'existence du sommet A.
Si BDC = 2α alors la somme des angles du triangle BDC est 5α = 180°, ce qui donne un angle α = 36°.
BDC est alors égal à 72°, c'est aussi l'angle extérieur de ABD, angle égal à ABD + BÂD, d'où BÂD = ABD = 36°, ABD est aussi isocèle. Le triangle ABC est un triangle d'or.
Conclusion : il n'y a que deux types de triangles bisocèles : le triangle d'or et le triangle isocèle rectangle.
WikiPédia : triangle isocèle
9.b. Tr. isocèles
À partir du centre du cercle circonscrit d'un triangle acutangle, on peut le partager en trois traits, en trois triangles isocèles.
Mais il n'est pas toujours possible de diviser, d'un seul trait, un triangle en deux triangles isocèles.
Quels sont les triangles isocèles que l'ont peut partager en deux tr. isocèles ?
Indications
Ci-dessus deux cas où la sécante est une bissectrice du triangle : ce sont les triangles bisocèles.
Une recherche analogue permet de trouver ci-dessous deux autres formes de tr. isocèles où les sécantes sont des trisectrices.
Trouver un tr. isocèle
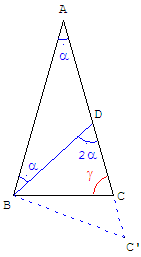
Comme ci-dessus, explorer le cas où un des triangles isocèles aura pour base [AB], l'autre pour base [BD].
Si D est le point d'intersection de la médiatrice de [AB] avec [AC],
ABD est un triangle isocèle d'angles α = BÂC = ABD.
Le supplément de l'angle au sommet est BDC = 2α.
La médiatrice de [BD] coupe (AC) en C’.
La trisectrice (BD) partage le triangle ABC’, d'angles α et 3α, en deux triangles isocèles.
Recherche d'un triangle isocèle :
déplacer le point A, de telle sorte que le point C’ coïncide avec le sommet C.
Télécharger la figure GéoPlan tr_isocele.g2w
Trisection d'un angle de la base
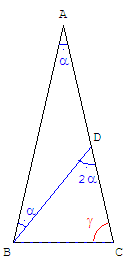
Angle en A égal à 
de l'angle plat,
soit α = 
radians.
Le triangle solution ABC, d'angles et γ = 
,
est partagé en deux triangles isocèles :
– d'angles 
et pour l'un,
– et 
pour l'autre.
Trisection de l'angle au sommet
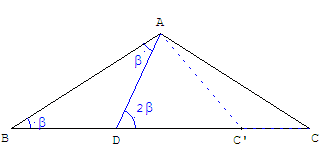
Cas où un des triangles isocèles aura pour base [AB], l'autre pour base [AD].
Si D est le point d'intersection de la médiatrice de [AB] avec [BC], ABD est un triangle isocèle d'angles β = ABC = BÂD = ABD.
Le supplément de l'angle au sommet est ADC = 2β.
La médiatrice de [AD] coupe (BC) en C’.
La trisectrice (AD) partage le triangle ABC’, d'angles β et 3β, en deux triangles isocèles.
Recherche d'un triangle isocèle : déplacer le point A, pour que C’ coïncide avec le sommet C.
Triangle d'argent
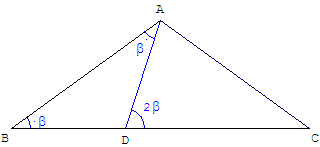
La sécante trisecte l'angle BÂC de 108°.
β = ABC = ACB = 36°.
ABC et DAB sont des triangles d'argent, CAD est un triangle d'or.
Télécharger la figure GéoPlan tr_isocele2.g2w
Conclusion
Il existe quatre formes de tels tr. isocèles :
– deux types de triangles bisocèles, partagés par une bissectrice : triangle d'or et demi-carré ;
– deux autres types de triangles, partagés par une trisectrice : le triangle d'argent et le triangle isocèle d'angle 180/7 degrés.
Table des matières
La fin du triangle : pour la recherche du mot « triangle », seulement trois résultats sur dix concernent la géométrie, et sans WikiPédia, le triangle mathématique disparaîtrait complètement !
Que penser de bing qui propose comme premier choix une boite d’intérim ?
Téléchargement
Télécharger triangle_college.doc : ce document au format « .doc »
Télécharger triangle_college.pdf : ce document au format « .pdf » d'Adobe Acrobat (bug de couleur de fond avec Word 2010)
Page no 72, réalisée le 19/7/2004
modifiée le 9/4/2012