L'espace de la sixième à la terminale… avec GeoGebra
Des idées de situations pour enseigner l'espace avec GeoGebra 3D, logiciel de géométrie dynamique.
Descartes et les Mathématiques
(Strato)
Présentation de GeoGebra 3D
Présentation
Logiciel libre
GeoGebra 3D au collège
La géométrie dans l'espace en sixième
La géométrie dans l'espace en cinquième
GeoGebra 3D au lycée
La géométrie dans l'espace en seconde
Section de tétraèdre par un plan
Section de cube en première
Produit scalaire en terminale
En projet :
figures GéoSpace en cours d'adaptation à GeoGebra 3D
…
…
Sur tablette numérique ou smartphone,
bascule automatique vers la version mobile
Technique interactive 2D-3D
GeoGebra 3D
Logiciel gratuit de géométrie dans l'espace
GeoGebra permet de créer, représenter et voir sous différents angles des figures de l'espace.
Celles-ci sont composées d'objets divers fixes ou variables : points, droites, plans, polygones…
Il intègre également la possibilité de créer et manipuler vecteurs, transformations, variables numériques, fonctions, etc.
La construction des principaux polyèdres y est facile et le logiciel gère correctement les arêtes et les faces cachées.
Les Outils 3D permettent de construire prisme, pyramide, cube, tétraèdre et leurs patrons.
Il aussi possible de construire dodécaèdre, icosaèdre et octaèdre.
La représentation des sphères, cylindres et cônes y est aussi pertinente.
GeoGebra permet trois modes de visualisation
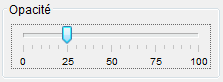
Dans les propriétés d'un objet , choisir l'onglet couleur et régler l'opacité :
- 0 pour une figure en fil de fer (on voit toutes les « lignes » en trait plein),
- 25 pour une figure transparente (les « lignes cachées » sont dessinées en pointillés),
- 100 pour une figure opaque (les « faces » et les « lignes cachées » disparaissent).
On peut faire tourner ces objets, les déplacer ou changer leur taille.
Ce que l'on voit sur l'écran est une représentation en perspective cavalière de l'objet étudié.
On peut aussi examiner les différents plans de la figure.
GeoGebra permet aussi d’effectuer des calculs de longueurs et de volumes.
Premiers pas dans l'espace : ne pas se noyer dans l'aquarium
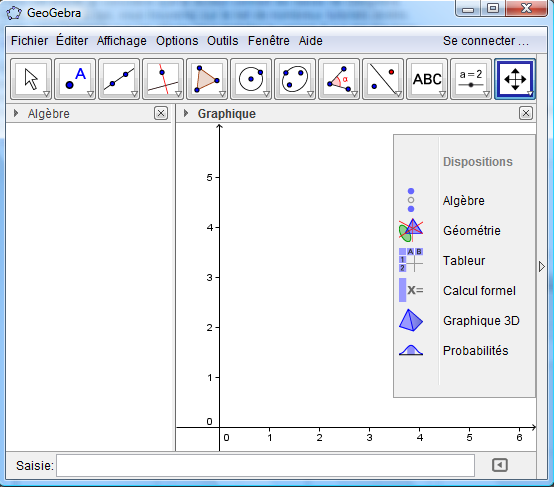
Fenêtres 2D et 3D
Au lancement de GGB, nous obtenons classiquement les deux fenêtres algèbre et graphique (2D).
Ajoutons, à l’aide du menu Affichage, la fenêtre Graphique 3D.
Tout objet graphique créé sera inséré automatiquement dans la fenêtre 3D.
S'il y a lieu, la partie de l'objet située dans le plan (xOy) sera affichée dans la fenêtre graphique (2D).
Il y a alors automatiquement, dans la fenêtre algébrique, l'expression de l'objet avec trois coordonnées.
De même un objet, créé dans la fenêtre graphique 2D, sera inséré dans le plan horizontal du graphique 3D et son expression, avec deux coordonnées, insérée dans la fenêtre algébrique.
Avec la ligne de saisie, il est aussi possible de créer une expression qui sera insérée dans la fenêtre algébrique et qui créera un objet géométrique dans la fenêtre 3D et éventuellement dans la fenêtre 2D.
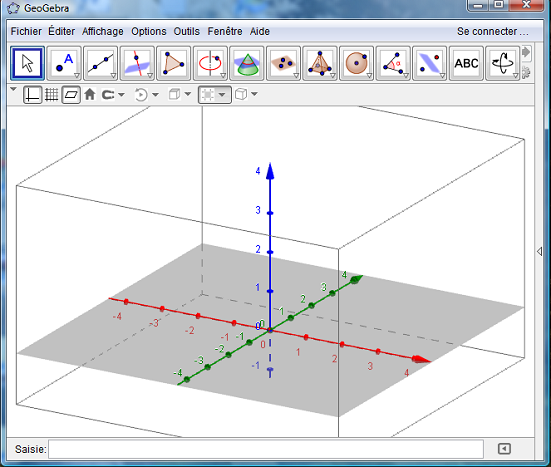
La fenêtre 3D contient une « boîte de visualisation » avec un repère 3D gradué.
C'est « l'aquarium » de diagonales Coin[-1,1] ; Coin[-1,3] en bas et Coin[-1,5] ; Coin|-1,7] en haut.
Le plan (xOy) y est grisé.
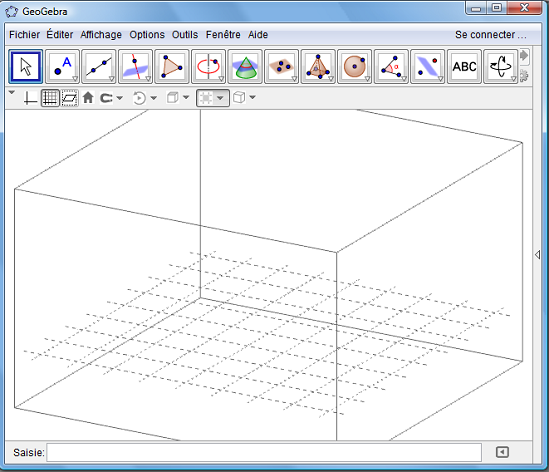
Utiliser la barre de style pour effacer les axes, faire apparaître la grille ou effacer le plan (xOy).
Pour effacer les contours de la « boîte de visualisation », cliquer sur l'icône « espace restreint ».
Clarifier la fenêtre 3D
Pointer dans la fenêtre 3D ; activer le menu écran en cliquant sur l'icône rotation.
Cliquer en dessous sur le bandeau 
pour faire apparaître la barre de style ci-dessous.
Cliquer dans les trois premières icônes pour supprimer les axes ; afficher la grille ; supprimer la grisaille du plan.
Pour effacer les contours de la « boîte de visualisation », cliquer sur l'icône 
à gauche du champ « espace restreint ». .
Il est conseillé de sauver cette figure vierge et la reprendre pour commencer un nouveau travail.
Présentation du logiciel
GeoGebra est un logiciel outil de construction géométrique.
Ce qui le caractérise est la séparation des objets géométriques et des objets informatiques.
Ce logiciel de construction a une double fonctionnalité :
- d'une part, celle de création d'objets mathématiques reliés éventuellement entre eux, avec un codage très proche de leur description en langage mathématique habituel.
- d'autre part, celle d'interprétation de ces objets pour en donner une représentation graphique dynamique, cette interactivité étant aussi exploitable sur Internet avec les ActiveX d'Internet Explorer.
Un outil pédagogique
Constituant une aide importante pour une meilleure appréhension des objets géométriques, GeoGebra 3D est précieux pour l'enseignement de la géométrie dans l'espace à tous les niveaux du collège au lycée.
Il permet de bien visualiser les différentes représentations d'un objet.
Les travaux permettront de retenir sous la forme d'images mentales, des situations d'incidence, d'orthogonalité ou de parallélisme qui seront facilement mise en œuvre en faisant tourner la figure ou par des vues de face dans la fenêtre graphique 2D.
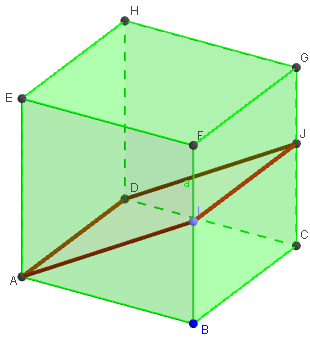
Figure : section du cube par un plan contenant une arête
Section d'un cube par un plan parallèle à une arête.
Figure 3D dans GeoGebraTube : rectangle comme section d'un cube
Figure géométrique
Coin de cube
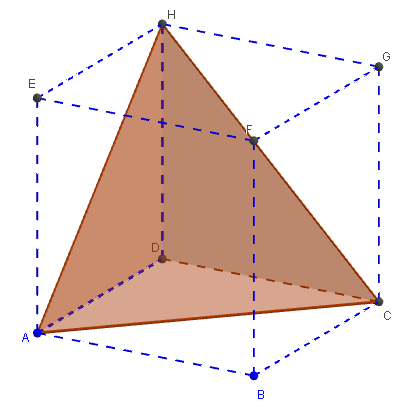
Beaucoup de problèmes de géométrie peuvent se traduire sous la forme de problèmes d'existence ou de construction d'une figure géométrique, en général, décrite implicitement par un texte ;
résoudre un problème avec ces outils est transformer cette description implicite en une description explicite avec les objets de GeoGebra.
L'apprentissage de GeoGebra devrait être réalisé, en travaux dirigés informatisés, dès la classe de sixième.
Figure 3D dans GeoGebraTube : coin de cube
Autre orientation : voir tétraèdre trirectangle
Trucs et astuces GeoGebra 3D
Savoir nommer certains objets
axes : axeX, axeY, axeZ ;
Le plan de base de la fenêtre graphique : PlanxOy
Les variables x, y et z sont réservés par le système et ne peuvent désigner des objets ou des nombres.
Commandes script
SoitValeur : voir le script par actualisation d'une case à cocher, pour afficher un tétraèdre régulier.
En projet
Patron d'un polyèdre
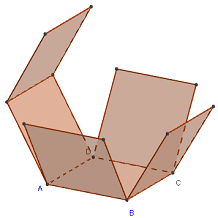
On obtient, parmi tous les patrons possibles, un patron choisi par le logiciel à partir de la face principale ayant servi à sa construction.
Les autres faces s'articulent autour de cette face.
Patron du cube
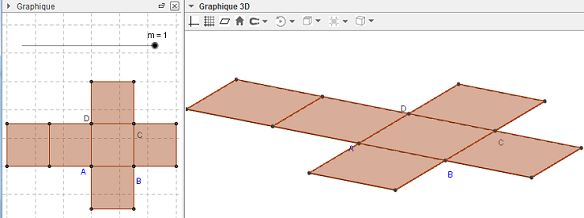
Le patron est piloté par un curseur m dans la fenêtre graphique.
Ouvrir le patron en faisant varier le coefficient d'ouverture m de 0 vers 1.
Pour m = 1 on trouve le patron ci-dessus.
Pour m = 0 on retrouve le cube.
Figure 3D dans GeoGebraTube : patron du cube
Exemples de figures dynamiques 3D avec GeoGebra Tube
GeoGebraTube : Pdebart
Lorsque vous utilisez une figure, pensez à « liker »
en cliquant sur l'icône 
Téléverser dans GeoGebraTube : voir GeoGebra 2D
Page Internet
GeoGebraTube
Index
Mode d'emploi de GeoGebra 3D
L'espace en sixième avec GeoGebra 3D
Figure copiée par : Marina ; la langue est l'italien, j'attends la traduction !
L'espace en cinquième avec GeoGebra 3D
Prisme vertical de base triangulaire
Patron de prisme de base triangulaire
Prisme horizontal de base triangulaire
L'espace en quatrième avec GeoGebra 3D
Pyramide de base carrée - plan diagonal
Trois pyramides inscrites dans un cube
Rectangle comme section d'un cube
Trapèze comme section plane d'un cube
Deux trapèzes comme section plane du cube
Parallélogramme ou pentagone comme sections planes du cube
Hexagone de Bergson comme section plane du cube
Section plane d'un parallélépipède rectangle
Section plane et tronc d'une pyramide de base carrée
Pyramide gauche de base carrée
Diagonales d'un prisme de base un trapèze
Théorème des trois perpendiculaires
triangle médian dans un coin de cube
Pentagone comme section du cube
Cube fortement tronqué - Sol LeWitt
Triangle comme section plane du cube
Sections d'un cube déterminées par trois points
Hexagone comme section d'un cube
Parallélogramme comme section d'un cube
Section d'un cube par un plan variable
Section d'un cube parallèle à trois diagonales de faces concourantes
Pentagone comme section d'un cube
Prolongement d'une section triangulaire du cube
Pentagone comme section du cube, 3 points sur 3 arêtes
Quatre hauteurs d'un tétraèdre
Bimédianes perpendiculaires d'un tétraèdre
Tétraèdre ayant deux hauteurs concourantes
Problèmes : p planxOy définit courbe implicite et
avec intersectionChemin[p,q] cliquer sur OK !
Deux arêtes orthogonales d'un tétraèdre
Pied de hauteur orthocentre de la base du tétraèdre
Bimédianes d'un tétraèdre orthocentrique
Perpendiculaires communes du tétraèdre orthocentrique
Sections de tétraèdre par un plan
Triangle comme section plane d'un tétraèdre
Section du tétraèdre par un plan parallèle à une arête
Parallélogramme comme section du tétraèdre
2 parallélogrammes sections planes du tétraèdre
Trois parallélogrammes sections planes du tétraèdre
3 parallélogrammes comme sections du tétraèdre
Quadrilatère comme section plane d'un tétraèdre
Trapèze comme section plane d'un tétraèdre
La géométrie dans l'espace en terminale S à l'épreuve pratique de mathématiques
Triangle équilatéral formé par trois diagonales de faces concourantes du cube
Partage en trois d'une diagonale du cube
Figures GeoGebraTube (en projet)
Diagonales d'un cube
en fil de fer
…Avec GeoGebra 2D
Page no 203, créée le 7/10/2014