Après la suppression des translations, rotations ou homothéties, la similitude est la seule transformation rescapée dans l'enseignement français, et seulement en enseignement de spécialité de terminale S, certainement pour justifier les nombreux exercices du bac avec la caractérisation complexe.
Dans le programme 2011, les similitudes directes sont introduites comme transformations du plan composées d'une homothétie et d'un déplacement. L'ennui est qu'homothétie et déplacement ne sont plus étudiés dans les programmes des classes antérieures : on n'est plus à une incohérence près !

Une similitude est une transformation du plan conservant les angles et les rapports de distances : qui multiplie les distances par une constante positive fixe k, le rapport de similitude.
L'image d'une figure par une similitude est une figure semblable, c'est-à-dire intuitivement « de même forme ».

Les similitudes directes, distinctes de l'identité et de la translation, admettent un unique point fixe.

1. Alignement avec un point et son transformé

transformation geometrique similitude - alignement avec un point et son transforme

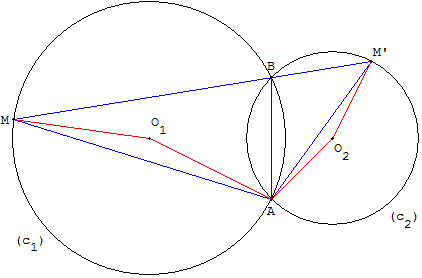
Un point A fixe et un point M variable sont placés sur un cercle (c₁).
Une similitude de centre A transforme le cercle (c₁) en un cercle (c₂) et le point M en un point M’.

Les cercles (c₁) et (c₂) ont comme deuxième point d'intersection B.

Montrer que les points M, B et M’ sont alignés.

Démonstration

Calculer l'angle (, ) = (, ) + (, ) [mod π].

Les angles inscrits sont égaux à la moitié de l'angle au centre :
(, ) = (, ) [mod π],
(, ) = (, ) [mod π].

Dans la similitude A est point fixe, O₁ a pour image O₂, M a pour image M’, par conservation des angles on a (, ) = (, ) [mod π].
D'où – (, ) = (, ) et (, ) = 0 [mod π] ce qui prouve l'alignement.

Figure interactive dans GeoGebraTube : alignement dans une similitude
(la similitude est la composée d'une rotation de centre A suivie d'une homothétie de centre A et de rapport r₂/r₁.
M a pour image M₁ par la rotation, M₁a pour image M’ par l'homothétie.)

Démonstration avec les angles inscrits, voir : angles inscrits en troisième,

cas particulier de cercles de même rayon : voir rotation en seconde,
exercice proposé à l'épreuve pratique de terminale S en 2009.

2. Déterminer le centre de similitude

transformation géométrique similitude - determiner le centre

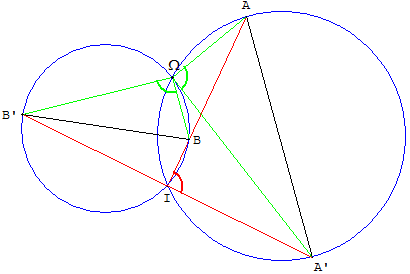
À partir de deux points et de leurs transformés, déterminer géométriquement le centre d'une similitude

Propriété : étant donné quatre points A, B, A’, B’ tel que A ≠ B, A’ ≠ B’ et que les droites (AB) et (A’B’) soient concourantes en point I, il existe une unique similitude plane directe s telle que s(A) = A’ et s(B) = B’.

L'angle α de la similitude est une des mesures de l'angle de la droite (AB) avec sa transformée (A’B’).

Le centre Ω de similitude est le deuxième point d'intersection des cercles circonscrits à AA’I et BB’I, cercles contenant les arcs capables d'où l'on voit les segments [AA’] et [BB’] selon l'angle α.

Indication

Les hypothèses évitent les transformations particulières, homothéties ou translations, où les droites (AB) et (A’B’) sont parallèles.

La démonstration se fait avec l'écriture complexe z’ = az +b d'une similitude.

Application

ÉduSCOL – Terminale S – Banque de sujets 2004 – Sujet 17

PARTIE I

ABC est un triangle rectangle en B, direct : (, ) =

Soit E un point du segment [AB]. Par le point E on mène une droite (d) qui coupe le segment [AC] en un point F et la droite (BC) en un point G (voir figureci-dessous). On suppose que les points E, F, G sont distincts des points A, B, C.

Le cercle Γ circonscrit au triangle ABC et le cercle Γ’ circonscrit au triangle BEG se coupent en deux points distincts B et K.

Justifier l'existence d'une similitude plane directe s telle que s(A) = C et s(E) = G.
Déterminer l'angle de s.

transformation géométrique similitude - centre

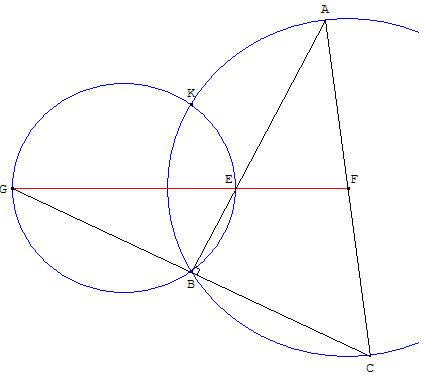
Soit Ω le centre de s.

Montrer que Ω appartient aux cercles Γ et Γ’.
Prouver que Ω est différent de B.
Que peut-on en déduire pour Ω ?

Télécharger la figure GéoPlan centre_similitude.g2w

PARTIE II

Le plan complexe est rapporté à un repère orthonormal direct (O ; , ) d'unité graphique 2 cm. Les affixes respectives des points A, B, C, E, F et G sont données par :

z_A = 2 + 4i, z_B = −l − 2i, z_C = 3 − 4i, z_E = 0, z_F = 5, z_G = −5.

On admettra que le point F est le point d'intersection du segment [AC] et de la droite (GE) et que les conditions de la partie I sont vérifiées.

Placer ces points sur une figure et, à l'aide des résultats de la partie I, construire le point Ω, centre de la similitude s.

Soit s’ la similitude plane directe telle que s’(A) = E et s’(C) = G. Déterminer l'écriture complexe de s’ et déterminer l'affixe du centre Ω’ de s’.
Montrer que les points Ω et Ω’ sont confondus.

Indications

Le centre Ω de la similitude s d'angle est le point K.
Partie 2 : L'écriture complexe de s’ est z’ = az +b avec a = (−1 − 8i)/13 et b = (−30 + 20i)/13
z_Ω’ = − l + 2i, les points Ω et Ω’ sont confondus avec K.

3. Deux carrés autour d'un rectangle

transformation géométrique similitude - deux carrés autour d'un rectangle

Homothétie, produit scalaire et similitude au bac S

Polynésie – septembre 2000

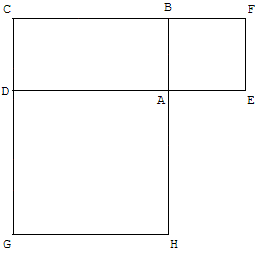
Sur la figure ci-contre, ABCD est un rectangle de sens direct, AEFB et ADGH sont des carrés de sens direct.

3.1. Le but de cette première question est de démontrer que les droites (AC), (EG) et (FH) sont concourantes.
Pour cela, on note I le point d'intersection des droites (EG) et (FH) ; puis on introduit :
− l'homothétie h₁ de centre I qui transforme G en E ;
− l'homothétie h₂ de centre I qui transforme F en H.
a. Déterminer l'image de la droite (CG) par l'homothétie h₁ puis par la composée h₂ o h₁.
b. Déterminer l'image de la droite (CF) par l'homothétie h₁ o h₂.
c. Justifier l'égalité h₂ o h₁ = h₁ o h₂.
En déduire que la droite (AC) passe aussi par le point I.

transformation géométrique similitude - médiane et hauteur dans deux carrés autour d'un rectangle

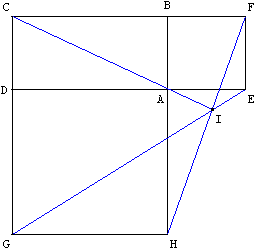
3.2. On se propose ici de démontrer que la médiane issue du sommet A du triangle AEH est une hauteur du triangle ABD.
On note O le milieu du segment [OH].
a. Exprimer le vecteur en fonction des vecteurs et .
b. Exprimer le vecteur en fonction des vecteurs et .
c. Calculer le produit scalaire . et conclure.

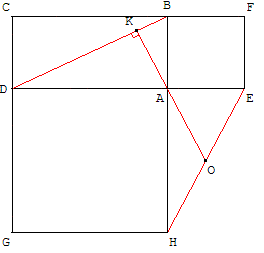
3.3. Dans cette question on étudie la similitude directe s qui transforme A en B et D en A.
On pose AB = 1 et AD = k (k > 0).
a. Déterminer l'angle et le rapport de la similitude s.
b. Déterminer l'image de la droite (BD), puis l'image de la droite (AO) par cette similitude s.
c. En déduire que le point d'intersection K des droites (BD) et (AO) est le centre de la similitude s.

Télécharger la figure GéoPlan homo_bac.g2w

Médiane de l'un, hauteur de l'autre : variante deux carrés autour du BOA

4. Deux carrés

Alignement avec un point de concours

Première Olympiade Internationale de Mathématiques – Bucarest 1959

Trois points I, A et G sont alignés si les droites (IA) et (IG) sont perpendiculaires à une même troisième.

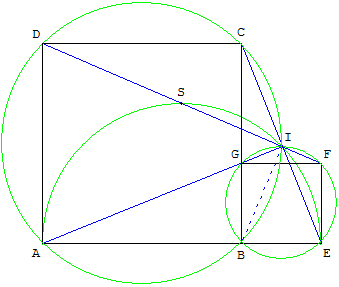
4.a. On considère deux carrés ABCD et BEFG, extérieurs l'un à l'autre, avec G ∈[BC].
Soit I le point d'intersection des deux segments [CE] et [DF].
Montrer que les points A, G et I sont alignés : les droites (CE), (DF) et (AG) sont concourantes en I.

Une figure riche : les droites (AG), (CE) et (DF) sont concourante en I.
Les angles FÎE, EÎB, BÎA, AÎD et DÎC mesurent 45°.
Le Point I est à l'intersection des cercles circonscrits aux carrés et du cercle de diamètre [AE].
Comme (BD) est perpendiculaire à (BF), les cercles circonscrits aux deux carrés sont orthogonaux.
Une similitude de centre I et d'angle transforme ABCD en EFGB.

Solution

La similitude de centre B et de rapport et d'angle transforme E en F, C en D, [EC] en [FD], d'où :
(, ) = = (, ) (modulo 2π).

Le point I est cocyclique avec E, F et G sur le cercle de diamètre [EG], d'où : (, ) = (2π).

On a, de même, (, ) = = (, ) (2π).

I est cocyclique avec A, C et D sur le cercle de diamètre [AC], d'où : (, ) = (2π).

(IA) et (IG) sont perpendiculaires à (EC) en I ; les points I, G et A sont alignés.

Télécharger la figure GéoPlan deux_carres.g2w

4.b. Intersection de tangentes

similitude - intersection de tangentes dans 2 carrés contigus

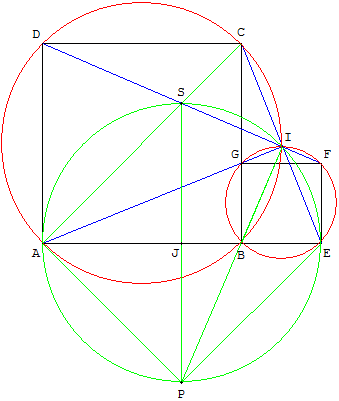
Autre démonstration pour le point I, avec des triangles isométriques

Les triangles rectangles ABG et CBE, ayant leurs petits côtés de même longueur que les côtés des carrés, sont isométriques.
Leurs côtés homologues sont perpendiculaires : comme (AB) est perpendiculaire à (BC) et (BG) à (BE), les hypoténuses (AG) et (EC) sont perpendiculaires et l'angle AÎE est droit.
Le point I est sur le demi-cercle supérieur de diamètre [AE],

Les angles AÎC et GÎE étant droits, le point I se trouve à la fois sur les cercles circonscrits aux carrés ABCD et BEFG, tout comme le point B, d'ailleurs.

Point P d'intersection de tangentes

Les tangentes en A et E à ces deux cercles circonscrits, perpendiculaires respectivement aux diamètres [AC] et [EG] (diagonales des carrés), font un angle de 45° avec l'horizontale (AE) et se coupent en P.

Le triangle APE a deux angles de 45° : il est rectangle isocèle. PA = PE car la distance de P aux deux points de tangence est la même.
Le point P est donc sur l'axe radical des deux cercles, la droite (IB).

Cercle de diamètre [AE]

Le cercle de diamètre [AE] coupe [DF] en I et S. Le point S est situé sur la diagonale [AC] du carré.
[SP] est un diamètre du cercle, perpendiculaire à [AE]. Le centre du cercle est J, milieu de [AC] et de [SP].

Commande GéoPlan

Taper P pour afficher/effacer le point P

4.c. Problèmes sur les configurations

Dossier n^o 17 du CAPES Externe de Mathématiques 2005 – Épreuve sur dossier
Étude de configurations à l'aide de différents outils

L'exercice proposé au candidat :
Dans la figure ci-dessus, le point B est un point du segment [AE] distinct de A et E.
ABCD et BEFG sont des carrés.
On se propose de démontrer, par différentes méthodes, que les droites (AG) et (EC) sont orthogonales.

4.c.a. Outil « configurations »
On note I le point d'intersection de (AG) et (EC). Justifier que l'angle AIE est droit et conclure (on pourra considérer le triangle GIE ? Voir plutôt ci-dessus).

4.c.b. Outil « produit scalaire »
Calculer . et conclure.

4.c.c. Outil « analytique »
Après avoir muni le plan d'un repère orthonormal, montrer que les droites (AG) et (EC) sont orthogonales.

Le travail demandé au candidat
Q.1. Mettre en évidence, à l'aide du logiciel de géométrie dynamique de la calculatrice, la propriété indiquée.
Q.2. Indiquer pour chacun des outils, le niveau où pourrait être donné l'exercice.
Q.3. Proposer une autre méthode de résolution.
Q.4. Proposer un ou plusieurs exercices qui permettent de mettre en jeu plusieurs méthodes pour résoudre un même problème de géométrie plane.

Indications

Pour le « produit scalaire », préférer le calcul vectoriel au calcul sur les coordonnées.

En « analytique » vérifier la relation mm’ = −1 pour les coefficients directeurs des deux droites.

Pour la question Q.3 on peut utiliser :
– les transformations : rotation de centre B ou similitude comme ci-dessus,
– les triangles semblables,
– les complexes.

5. Pseudo-carré

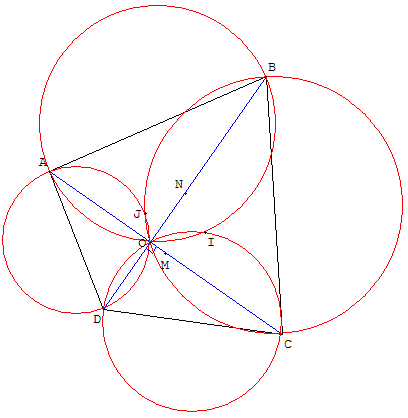
Bac S Antilles-Guyane – Septembre 2002 : exercice pour les candidats ayant suivi l'enseignement de spécialité.

Dans le plan on considère deux segments [AC] et [BD] tels que :
AC = BD et (, ) = − (ABCD est un pseudo-carré).
On désigne par M le milieu de [AC] et par N celui de [BD].
On appelle (c₁), (c₂), (c₃) et (c₄) les cercles de diamètres [AB], [BC], [CD] et [DA].

5.1.a. Soit r la rotation qui transforme A en B, C en D.
Quel est l'angle de r ?
Montrer que le centre I de r appartient aux cercles (c₁) et (c₃).

5.1.b. Soit r’ la rotation qui transforme A en D, C en B.
Quel est l'angle de r’ ?
Montrer que le centre J de r’ appartient aux cercles (c₂) et (c₄).

5.1.c. Quelle est la nature du quadrilatère INJM.

On désigne par P et R les points diamétralement opposés à I sur, respectivement, (c₁) et (c₃) et par Q et S les points diamétralement opposés à J sur, respectivement, (c₂) et (c₄).

5.2. Soit s la similitude directe de centre I, de rapport et d'angle .
5.2.a. Quelles sont les images par s des points D, N, B ?
5.2.b. En déduire que le point J est le milieu de [PR].

Télécharger la figure GéoPlan quadri_ortho.g2w

transformation géométrique similitude - pseudo-carré

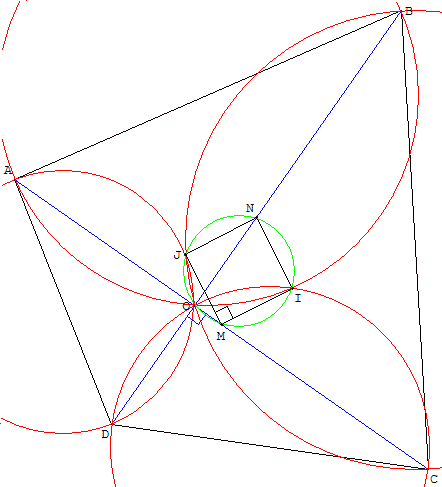
5.1.a. Rotation qui transforme en :
L'angle de la rotation est l'angle des deux vecteurs soit –.
(, ) = − , le centre I est sur le cercle de diamètre [AB] : I est donc sur (c₁).
On montre, de même, que I est sur (c₃).
5.1.b. La rotation r’ transforme en . Son angle est et son centre J est l'intersection des cercles (c₂) et (c₄), autre que O.

5.1.c. Les rotations r et r’ transforment [AC] en [BD]. Le milieu M de [AC] est transformé en N milieu de [BD].
Pour r : IN = IM et l'angle MIN est droit, pour r’ : JN = JM et l'angle MJN est droit. Les points I et J sont les intersections de la médiatrice de [MN] avec le cercle diamètre [MN].
INJM est un carré.

Comme l'angle MON est droit, le point O est situé sur le cercle de [MN] circonscrit au carré. Dans ce cercle les angles inscrits ION et IMN sont égaux, donc égaux à .

5.2.a. Dans le carré INJM, IJ = IN avec un angle NIJ de . La similitude s transforme N en J.
Dans le cercle (c₁) de diamètre [AB], l'angle ION est l'angle inscrit IOB, comme on vient de le voir au paragraphe précédent, il est égal à . Le point I est le milieu du demi-cercle (AIB). Le point P symétrique de I est aussi le milieu le l'autre demi-cercle (APB).
L'angle inscrit PIB vaut et le triangle rectangle IBP est isocèle.
La similitude s transforme B en P.
On montre, de même, que IDR est un triangle rectangle isocèle : s transforme D en R.

5.2.b. La similitude s transforme B, N, D en P, J, R. Comme N est le milieu de [BD], J est alors le milieu de [PR].

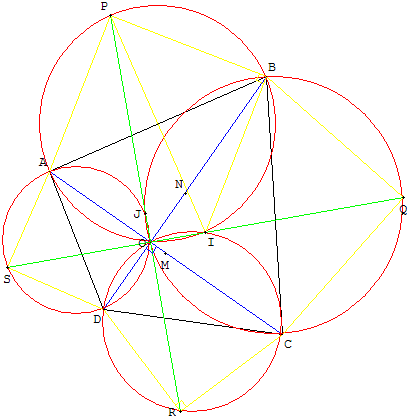
Remarque : on peut aussi montrer que la similitude directe s’ de centre J, de rapport et d'angle , transforme A, M, C en S, I, Q.
I est le milieu de [SQ].

On a donc PR = SQ = BD = AC. (PR) et (SQ) sont perpendiculaires et sont les bissectrices de (AC, BD).

On retrouve la configuration de Van Aubel.

Voir aussi : droite de Van Aubel dans le triangle

6. Droites perpendiculaires dans un triangle isocèle

similitude transformation géométrique - droites perpendiculaires dans un triangle isocèle

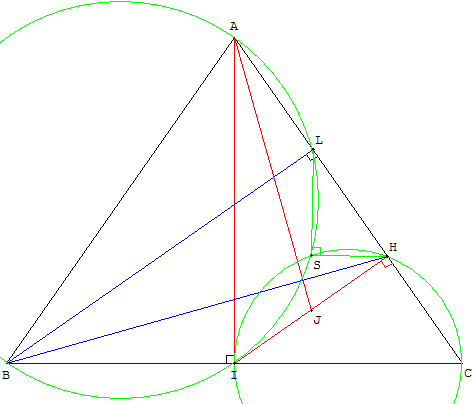
Trois méthodes pour résoudre un même exercice :
– ici l'utilisation d'une similitude transformant deux triangles semblables
– voir l'exploitation des configurations fondamentales, dans triangle en second

– voir aussi en 1^ère S, une démonstration par le calcul d'un produit scalaire nul

Exercice

Soit ABC un triangle isocèle en A, I le milieu de [BC], H le projeté orthogonal de I sur (AC), J le milieu de [IH].

Montrer que les droites (AJ) et (BH) sont perpendiculaires.

Indications

Tracer la hauteur [BL] du triangle ABC et étudier les triangles rectangles AHI et BLC.

Ces triangles, ayant leurs côtés deux à deux perpendiculaires, sont semblables.
Une similitude d'angle transforme AHI en BLC. Son centre S est à l'intersection des cercles de diamètres [AB] et [IC].
Par cette similitude, la médiane [AJ] de AHI a pour image la médiane [BH] de BLC.

L'angle d'une droite et de son image est égal à l'angle de la similitude, et on a bien (AJ) perpendiculaire à (BH).

Télécharger la figure GéoPlan confond.g2w

L@ feuille à problèmes : utilisation d'une similitude