|
Voici quelques configurations pouvant facilement s'étudier de diverses manières : autrefois avec les transformations (rotations – homothéties), le produit scalaire en première S ou les complexes en terminale S.
Deux carrés autour de BOA
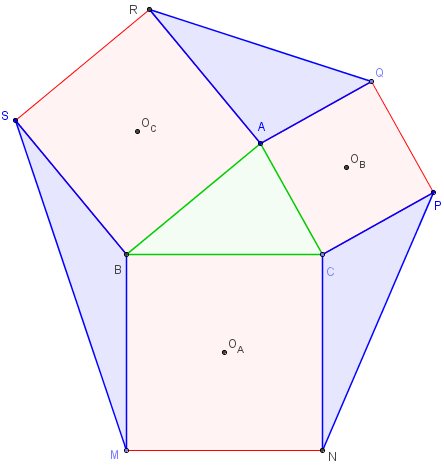
Un triangle, deux carrés autour du triangle : une configuration d'une grande richesse où les 5 exercices ci-dessous conduisent à 15 sujets pouvant être traités aux trois niveaux du lycée.
|
|
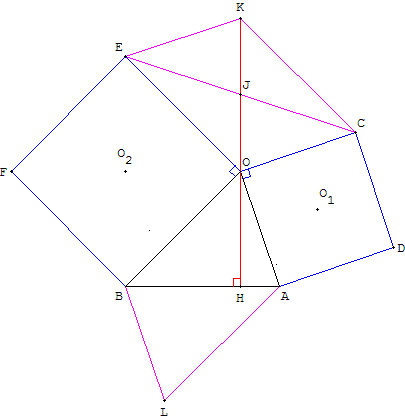
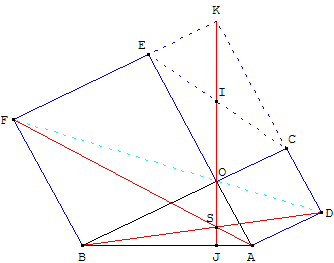
BOA est un triangle quelconque tel que ( , , 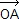 ) = α (α ∈]0, π[) ) = α (α ∈]0, π[)
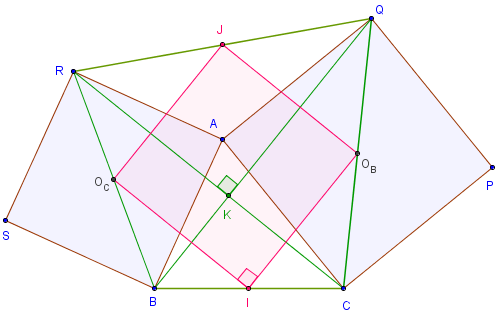
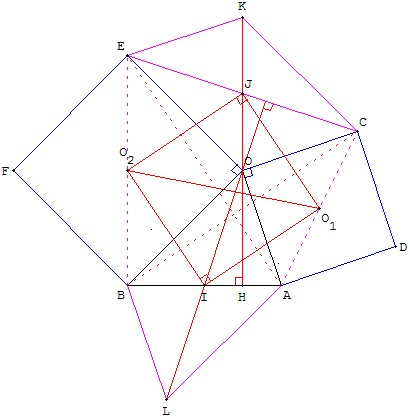
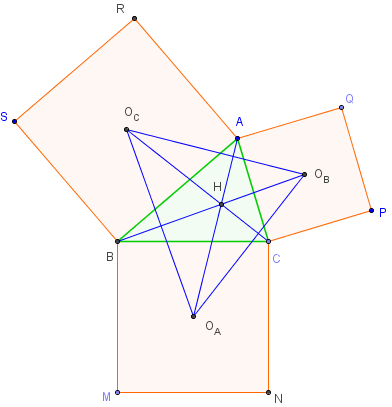
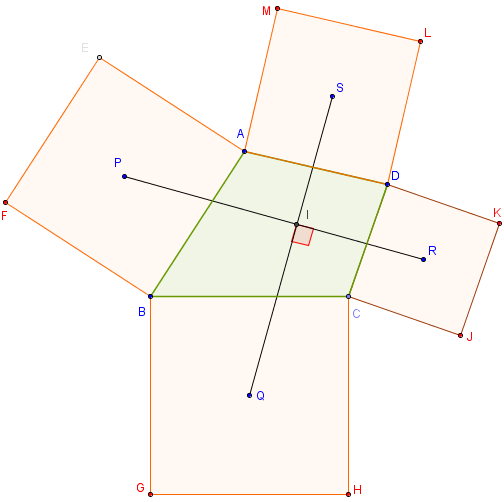
On construit extérieurement à ce triangle les carrés OADC et BOEF de centres respectifs O1 et O2.
On construit aussi le parallélogramme EOCK de centre J
et le parallélogramme BOAL de centre I.
Montrer que la droite (OJ) est une hauteur du triangle BOA et que OK = AB.
Indications
La rotation de centre O et d'angle 90° transforme A en C.
La translation de vecteur 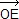 transforme C en K. transforme C en K.
La composée de ces deux transformations transforme A en K, O en E.
C'est une rotation d'angle 90° ; son centre est O2. B a donc pour image O ;
[BA] a pour image [OK] ; d'où BA = OK et (BA) est perpendiculaire à (OK).
 Figure interactive dans GeoGebraTube : hauteur de l'un, médiane de l'autre Figure interactive dans GeoGebraTube : hauteur de l'un, médiane de l'autre
Variante 1 : Utiliser l'invariance d'un carré dans la rotation d'angle 90°, de centre le milieu du carré.
La rotation de centre O2, qui transforme B en O, transforme [BO] en [OE].
De plus, les angles OBL et EÔC sont égaux (ayant même supplémentaire AÔB)
et CK = OE = OB = AL.
Donc, par la rotation, le parallélogramme OBLA a pour image EOCK, et [BA] a pour image [OK].
Dès lors, OK = AB et (OJ) est perpendiculaire à (AB).
Variante 2 : démonstration avec une rotation de centre O, voir la médiane de l'un est la hauteur de l'autre
|
|
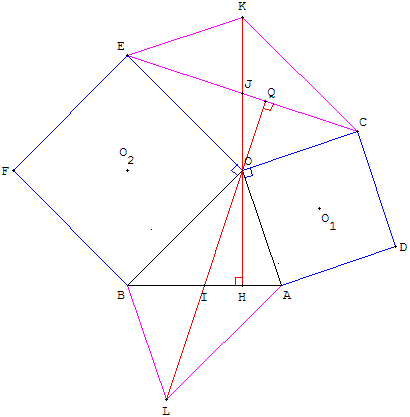
Dualité
– La médiane [OJ] du triangle COE est hauteur du triangle BOA.
– La médiane [OI] du triangle BOA est hauteur du triangle COE
et CE = OL = 2 OI.
 Figures interactives dans GeoGebraTube : deux carrés autour d'un triangle - hauteurs - médianes Figures interactives dans GeoGebraTube : deux carrés autour d'un triangle - hauteurs - médianes
deux triangles rectangles, parallélogrammes, hauteurs, médianes
|
|
Classe de première S - produit scalaire
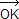 = = 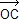 + + 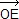 ; ; 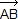 = = 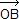 - - 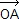 ; a = OA ; b = OB, c = AB. ; a = OA ; b = OB, c = AB.
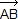 . .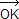 = ( = (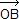 - - 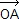 ).( ).(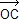 + + 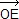 ) = ) = 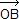 . .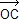 + 0 - 0 - + 0 - 0 - 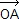 . .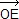
= ab cos(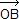 , , 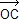 ) - ab cos( ) - ab cos(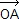 , , 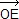 ) = ab {cos(α+π/2) - cos [(π-α)+π/2]} = 0 donc (AD) est perpendiculaire à (BC). ) = ab {cos(α+π/2) - cos [(π-α)+π/2]} = 0 donc (AD) est perpendiculaire à (BC).
Al-Kashi permet de calculer AB2 : c² = a² + b² - 2 ab cos α,
OK2 = (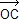 + + 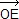 )2 = OC2 + OE2 + 2 ab cos( )2 = OC2 + OE2 + 2 ab cos(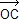 , , 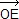 ) et comme cos( ) et comme cos(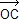 , , 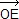 ) = cos(π-α) = − cos α on a AD2 = c2 et AD = BC = c. ) = cos(π-α) = − cos α on a AD2 = c2 et AD = BC = c.
TS - nombres complexes
L'apport des complexes est la grande simplicité des calculs et la mise en évidence directe de la rotation z’ = iz.
Prendre O comme origine, les affixes des points sont notées par les minuscules correspondantes.
c = ia, e = −ib donc k = i(a−b) ; d'où |k| = |a−b| avec |k| = OK, |a−b| = AB,
soit OK = AB ; arg(k) = 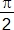 + arg(a−b) d'où ( + arg(a−b) d'où (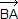 , , 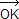 ) = ) = 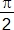 (2π). (2π).
|
|
Complexes : bac S, Toulouse 1985
Construction de deux carrés OADC et OEFB à l'extérieur du triangle BOA.
Le point K complète le parallélogramme EOCK.
Montrer que les droites (BD) et (AK) sont perpendiculaires, et que BD = AK,
de même (AF) et (BK) sont aussi perpendiculaires et AF = BK.
Indication
Les triangles BAD et KOA sont isométriques et ont leurs côtés deux à deux perpendiculaires.
Étude des triangles rectangles isocèles OO1A et OO2B, voir triangles autour d'un triangle BOA
cas particulier : BOA rectangle en O, voir Renan
 Télécharger la figure GéoPlan ca_boa_2.g2w Télécharger la figure GéoPlan ca_boa_2.g2w
|
|
Solution
Soit BARS le carré de côté [BA], de centre O3, situé du même côté de (BA) que O.
La rotation de centre O3 et d'angle 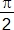 transforme B en A, A en R. transforme B en A, A en R.
AR = BA = OK et (AR), perpendiculaire à (BA), est parallèle à (OK),
AOKR est donc un parallélogramme,
d'où KR = OA = AD et (KR), parallèle à (OA), est perpendiculaire à (AD).
L'image de D par la rotation est donc K, [BD] a pour image [AK] :
(BD) et (AK) sont perpendiculaires et BD = AK.
Remarques : Le triangle SKR, translaté du triangle BOA, est isométrique à BOA.
FKD est un triangle rectangle isocèle en K : voir 3.
|
|
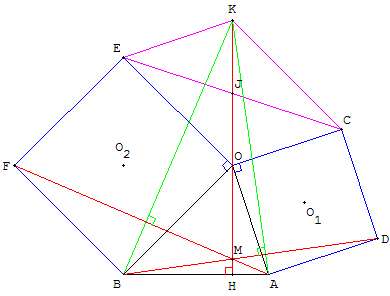
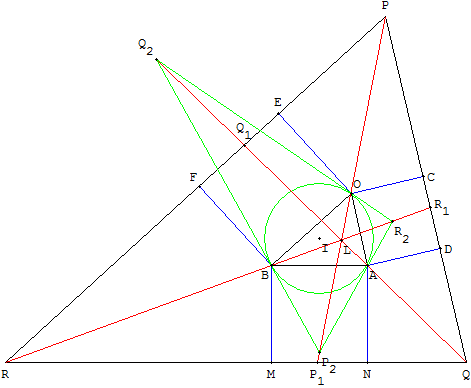
Les droites (BD) et (AF) sont concourantes en M.
Montrer que la droite (OM) est orthogonale à (AB).
Indication
Le point M est situé sur (OK), hauteur de BOA qui est aussi une médiane de OCE.
En effet, M commun aux hauteurs (AF) et (BD) est l'orthocentre du triangle ABK. (KM) est la troisième hauteur perpendiculaire à (AB) issue de K.
On a vu au paragraphe 1 que les points O, J sont alignés sur une perpendiculaire à (AB) passant par K, la droite (KM).
O et M sont donc deux points de cette droite perpendiculaire à (AB) : (OM) est donc perpendiculaire à (AB).
Autre formulation avec des triangles rectangles isocèles :
BOA est un triangle quelconque, OAD et OFB sont deux triangles rectangles isocèles directs, respectivement en A et B. Le point M est l'intersection des droites (BD) et (AF). Montrer que la droite (OM) est orthogonale à (AB).
Remarque : au paragraphe 6, on montrera avec la figure des extriangles, que les triangles BOA et OCE ont même aire.
|
|
Classe de 2nde
Soit I le milieu de [AB], O1 et O2 les centres des carrés.
Le triangle IO1O2 est rectangle isocèle.
En effet, la rotation de centre O et d'angle 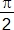 transforme E en B, A en C, [AE] en [BC]. Ces segments sont de longueur égale et orthogonaux.
transforme E en B, A en C, [AE] en [BC]. Ces segments sont de longueur égale et orthogonaux.
Le quadrilatère ABEC est un pseudo-carré (quadrilatère orthodiagonal à diagonales de même longueur).
Il est de même pour [IO1] et [IO2], segments des droites des milieux des triangles BAC et ABE, respectivement parallèles aux segments précédents et de longueurs moitiés.
 Figure interactive dans GeoGebraTube : deux carrés autour d'un triangle et Varignon Figure interactive dans GeoGebraTube : deux carrés autour d'un triangle et Varignon
Retrouver cette configuration avec les demi-carrés OAC et OBE comme triangles rectangles isocèles autour de BOA
Étude des triangles rectangles isocèles OO1A et OO2B, voir que de triangles rectangles isocèles
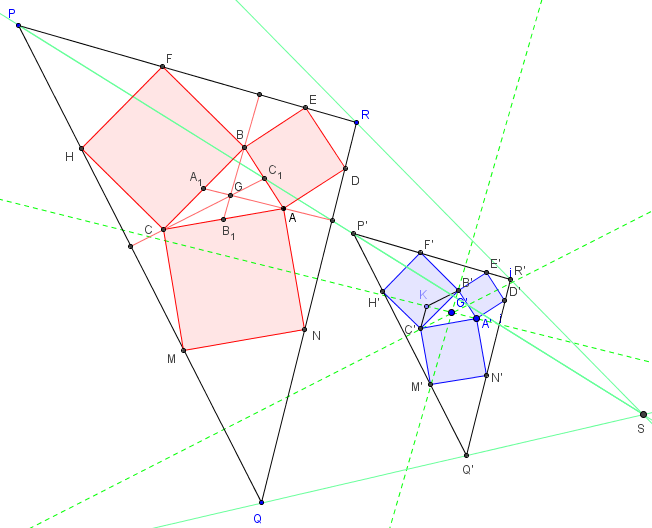
Variante : on peut considérer la configuration formée par deux carrés ayant en commun un sommet et deux parallélogrammes (voir figure ci-contre).
Montrer que les centres des carrés et des parallélogrammes sont les sommets d'un carré.
Indications
Le théorème de Varignon affirme que IO1JO2 est un parallélogramme dont les côtés sont parallèles aux diagonales [AE] et [BC] du quadrilatère BACE, avec IO1 = BC/2 et IO2 = AE/2.
Nous avons montré ci-dessus que ces deux diagonales sont de longueurs égales et perpendiculaires ce qui permet d'assurer que IO1JO2 est un carré.
Le concours EPF de 2003 propose un repère d'origine O et d'introduire les affixes des points A, C, B et E (voir : annales ABC bac S - Nathan).
 Télécharger la figure GéoPlan ca_boa_6.g2w Télécharger la figure GéoPlan ca_boa_6.g2w
|
|
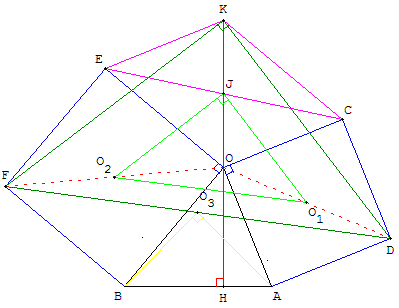
Construction de deux carrés OADC et OEFB à l'extérieur du triangle BOA.
Le point K complète le parallélogramme EOCK.
Montrer que le triangle DFK est rectangle isocèle.
Indication
L'homothétie de centre O de rapport 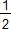 transforme DFK en O1O2J, triangle dont les sommets sont les milieux des carrés et du parallélogramme. Ce triangle, moitié du carré de Varignon étudié ci-dessus, est un triangle isocèle rectangle. transforme DFK en O1O2J, triangle dont les sommets sont les milieux des carrés et du parallélogramme. Ce triangle, moitié du carré de Varignon étudié ci-dessus, est un triangle isocèle rectangle.
Remarque
Le point O3, milieu de [DF] est le sommet d'un triangle rectangle isocèle d'hypoténuse [AB]. Voir 2.a.
 Télécharger la figure GéoPlan ca_boa_3.g2w Télécharger la figure GéoPlan ca_boa_3.g2w
|
|
Construction de deux carrés OADC et OEFB à l'extérieur du triangle BOA.
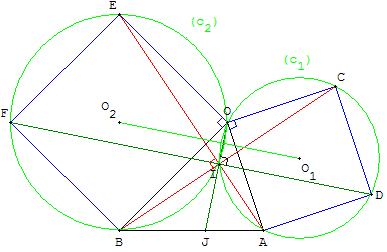
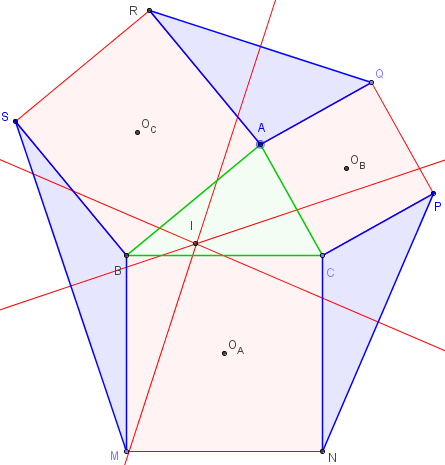
Les droites (BC), (AE) et (DF) sont concourantes en I.
On a démontré dans les triangles du BOA - chapitre 1, que les droites (BC) et (AE) sont perpendiculaires.
On montre que les droites (OI) et (DF) le sont aussi.
Les droites (OI) et (DF) sont les bissectrices des droites (BC) et (AE) et réciproquement.
Les angles aigus formés par ces droites sont égaux à  . .
La démonstration se fait en remarquant que I est le deuxième point d'intersection des deux cercles c1 et c2 circonscrits aux carrés puis en étudiant les angles inscrits dans ces cercles : les angles OÎD et OÎF, interceptant des demi-cercles, sont égaux à 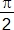 et les angles aigus en Î, interceptant des quarts de cercle, sont égaux à et les angles aigus en Î, interceptant des quarts de cercle, sont égaux à  . .
O1 et O2 étant les centres des cercles c1 et c2, la droite (O1O2) est parallèle à (DF) et est perpendiculaire à (OI).
 Télécharger la figure GéoPlan ca_boa_5.g2w Télécharger la figure GéoPlan ca_boa_5.g2w
|
|
Construction de deux carrés OADC et OEFB à l'extérieur du triangle BOA rectangle en O.
Le but de l'exercice est de montrer que les droites (OK), (AF) et (BD) sont concourantes.
Pour cela, on appelle S l'intersection de (AF) et (BD) ; puis on définit :
h1 : l'homothétie de centre S qui transforme D en B,
h2 : l'homothétie de centre S qui transforme F en A.
On utilise le fait que l'image d'une droite par une homothétie est une droite parallèle et que la composée de deux homothéties de même centre est une homothétie de même centre.
La médiane [OI] de COE est hauteur du triangle BOA.
 Télécharger la figure GéoPlan vecten_d.g2w Télécharger la figure GéoPlan vecten_d.g2w
Nombres complexes : bac S national 2005
Figure de Renan : démonstration du théorème de Pythagore, par la méthode des aires
|
|
BOA triangle rectangle - Calcul d'angles
Classe de seconde
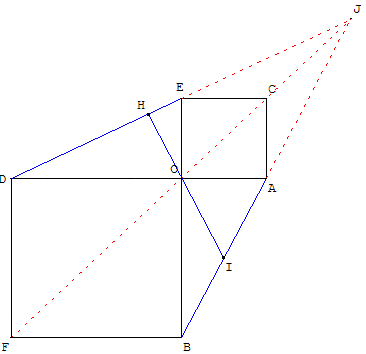
OACE et ODFD sont deux carrés de sens direct aux côtés parallèles, ayant uniquement le sommet O en commun.
Lorsque les carrés sont inégaux, les droites (AB) et (DE) se coupent en J.
Les points J, C, O et F sont alors alignés.
La médiane [OI] de BOA est hauteur du triangle DOE.
 Télécharger la figure GéoPlan homo_bac_boa.g2w Télécharger la figure GéoPlan homo_bac_boa.g2w
Indication
Pour montrer que la hauteur (OH) est perpendiculaire à (DE), utiliser la propriété du triangle rectangle vue au collège : « le milieu de l'hypoténuse est équidistant des trois sommets », d'où des triangles isocèles, puis des égalités d'angles…, jusqu'à conclure avec des angles complémentaires.
Variante : utilisation d'une similitude au bac
Retrouver cette configuration dans : carré au collège
|
6. Figure de Vecten (1817)
Construction de trois carrés BARS, CBMN et ACPQ à l'extérieur du triangle ABC.
6.a. Figures dites du moulin à vent d'Euclide
Les segments [AOA] et [OBOC] sont de même longueur et orthogonaux.
 Figure interactive dans GeoGebraTube : figure de Vecten - deux segments orthogonaux Figure interactive dans GeoGebraTube : figure de Vecten - deux segments orthogonaux
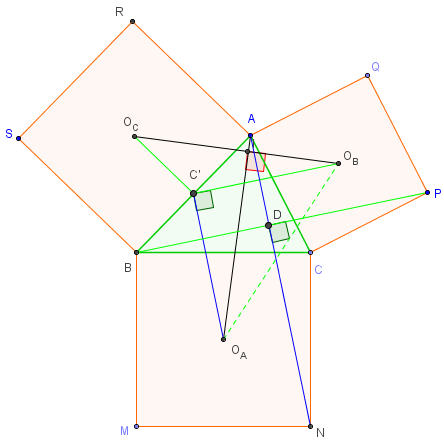
Démonstration par des rotations
Rotation de centre C et d'angle π/2
Soit C’ le milieu de [AB].
La rotation de centre C et d'angle 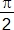 transforme P en A et B en N. transforme P en A et B en N.
Le segment [PB] et son image [AN] sont orthogonaux et de même longueur. La droite des milieux appliqué au triangle ABP montre que [C’OB] est parallèle à [BP] et égal à sa moitié.
De même dans le triangle ABN ; [C’OA] est parallèle à [BP] et égal à sa moitié.
Les segments [C’OA] et [C’OB] sont orthogonaux et de même longueur.
Au passage le triangle C’OAOB est rectangle isocèle.
Rotation de centre C' d'angle -π/2
OC a pour image A et OB a pour image OA.
Les segments [OCOB] et [AOA] sont orthogonaux et de même longueur.
 Figure interactive dans GeoGebraTube : figure de Vecten - démonstration de l'orthogonalité par les rotations Figure interactive dans GeoGebraTube : figure de Vecten - démonstration de l'orthogonalité par les rotations
|
|
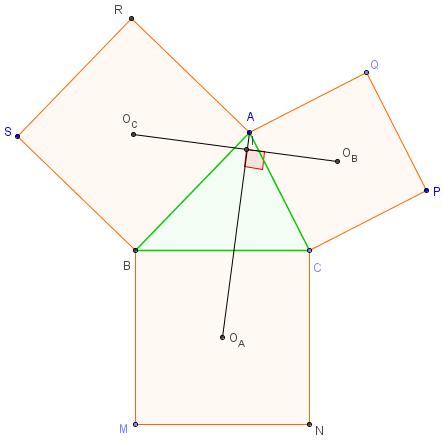
À l'extérieur d'un triangle ABC, on élève trois carrés, de centres OA, OB, OC, sur les trois côtés du triangle.
Les droites joignant les centres des carrés aux sommets opposés des triangles sont concourantes : leur point d'intersection s'appelle le point de Vecten du triangle.
Le triangle OAOBOC est le triangle de Vecten du triangle ABC.
Les hauteurs du triangle OAOBOC sont les droites (AOA), (BOB) et (COC) ;
H, orthocentre de OAOBOC, est le point de Vecten du triangle ABC.
Le triangle ABC et le triangle Vecten ont même centre de gravité.
Le cercle circonscrit au triangle de Vecten est le cercle de Vecten.
 Figure interactive dans GeoGebraTube : point de Vecten Figure interactive dans GeoGebraTube : point de Vecten
Point intérieur de Vecten
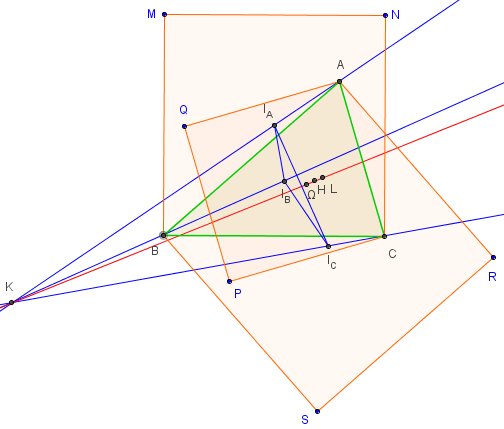
Construction de trois carrés BCNM, ABSR et CAQP du même côté que le triangle ABC.
Le triangle et les carrés sont de sens direct et de centres respectifs IA, IB et IC.
Le triangle IAIBIC est le triangle intérieur de Vecten du triangle ABC.
Les hauteurs du triangle IAIBIC sont les droites (AIA), (BIB) et (CIC) ;
Le point K, orthocentre de IAIBIC, est le point intérieur de Vecten du triangle ABC.
Le triangle ABC et le triangle intérieur de Vecten ont même centre de gravité.
Le cercle circonscrit au triangle intérieur de Vecten est le cercle intérieur de Vecten.
Droite de Vecten
Les deux points de Vecten sont alignés et en division harmonique avec le point de Lemoine et le centre du cercle d'Euler.
Pour ETC les points de Vecten sont X(485) et X(486) ; et sont alignés sur la droite X(5)X(6).
On trouve aussi sur cette droite le point de Prasolov X(68) et X(155) EIGENCENTER OF ORTHIC TRIANGLE
 Figure interactive dans GeoGebraTube : point intérieur de Vecten Figure interactive dans GeoGebraTube : point intérieur de Vecten
Voir trois triangles rectangles isocèles autour de BOA
WikiPédia : Point de Vecten
|
|
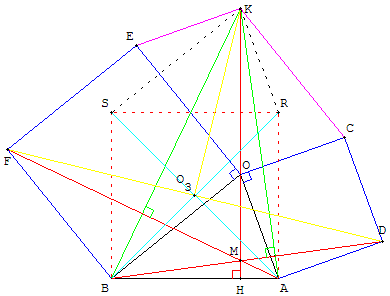
Solution par composition de similitudes
En examinant la figure ci-dessus à gauche, on voit que la similitude S(B, 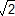 , ,  ) transforme le triangle OBO1 en EBA ) transforme le triangle OBO1 en EBA
et la similitude S(O, 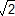 , - , -  ) transforme le triangle O3BO2 en AOE. ) transforme le triangle O3BO2 en AOE.
En composant la similitude de centre B suivie de la réciproque de la similitude de centre O on a :
|
S(B, 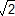 , ,  ) ) |
|
S(O, 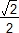 , ,  ) ) |
|
O |
→ |
E |
→ |
O2 |
O1 |
→ |
A |
→ |
O3 |
| [OO1] |
→ |
[EA] |
→ |
[O2O3] |
La composée de ces deux similitudes est une rotation d'angle 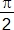 , [OO1] et [O2O3] sont de même longueur et orthogonaux. , [OO1] et [O2O3] sont de même longueur et orthogonaux.
On raisonne de même pour [AO2] et [O1O3] ; [BO3] et [O1O2].
|
|
Solution par calcul d'affixes de complexes
Les affixes des points sont notées par les minuscules correspondantes.
Le vecteur 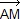 est directement orthogonal au vecteur est directement orthogonal au vecteur 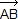 donc m – a = i(b – a). O1 est le milieu de [BM] donc son affixe o1 vérifie : donc m – a = i(b – a). O1 est le milieu de [BM] donc son affixe o1 vérifie :
2o1 = b + m = b + a + i(b – a) = b(1 + i) + a(1 – i).
De même, le vecteur 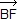 est orthogonal au vecteur est orthogonal au vecteur 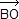 donc f – b = i(o – b). O2 est le milieu de [FO] donc o2 vérifie : donc f – b = i(o – b). O2 est le milieu de [FO] donc o2 vérifie :
2o2 = o + f = o + b + i(o – b) = o(1 + i) + b(1 – i).
Et comme 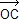 est orthogonal à est orthogonal à 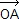 , on a c – o = i(a – o). , on a c – o = i(a – o).
O3 est le milieu de [CA], et o3 vérifie :
2o3 = a + c = a + o + i(a – o) = a(1 + i) + o(1 – i).
On a donc 2(o2 – o3) = 2oi + b(1 – i) – a(1 + i)
et 2(o – o1) = 2o – b(1 + i) – a(1 – i) = i 2(o2 – o3)
Les segments [O2O3] et [OO1] sont de même longueur et leurs supports sont orthogonaux.
Voir : plan complexe
|
|
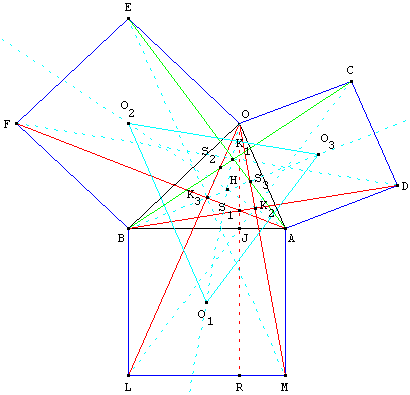
Rotation : La rotation de centre A et d'angle 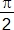 transforme [DB] en [OM]. BD = OM et les droites (BD) et (OM) sont orthogonales. transforme [DB] en [OM]. BD = OM et les droites (BD) et (OM) sont orthogonales.
De manière analogue la rotation de centre B et d'angle 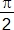 transforme [OL] en [FA]. AF = OL et les droites (AF) et (OL) sont orthogonales. transforme [OL] en [FA]. AF = OL et les droites (AF) et (OL) sont orthogonales.
Les droites (AF) et (BD) se coupent en S1 situé sur la hauteur (OJ) du triangle BOA.
Soit O1 le centre du carré ABLM.
Nous avons montré dans la figure du paragraphe 5, que les droites (AE), (BC) et (FD) sont concourantes en K1 et que ces droites
avec la droite (OK1) formaient des angles aigus de  . .
Nous trouvons ici que K1 est situé sur la droite (OO1).
Mêmes raisonnements avec les deux autres carrés :
(OS1), (AS2) et (BS3) sont les hauteurs du triangle BOA.
Le triangle O1O2O3 a ses côtés parallèles aux droites (EM), (CL) et (DF).
 Télécharger la figure GéoPlan vecten_2.g2w Télécharger la figure GéoPlan vecten_2.g2w
|
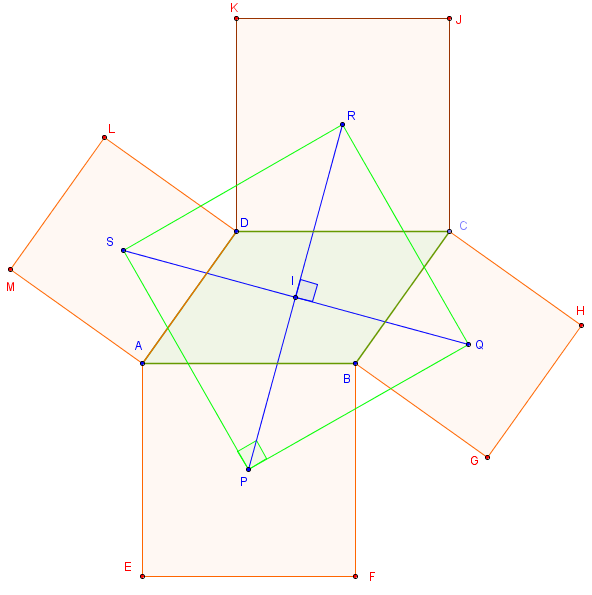
6.c. Moulin à vent bordé de parallélogrammes
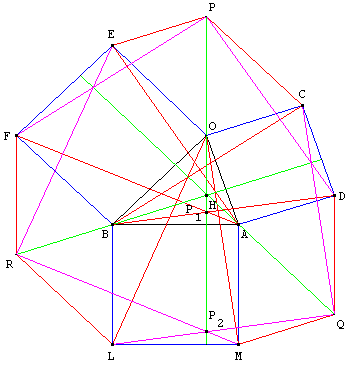
Compléter avec les points P, Q et R en construisant les parallélogrammes COEP, DAMP et FBLR.
Les droites (OP), (AQ) et (BR) sont les hauteurs de BOA.
La hauteur (OP) contient le point P1 intersection de (AF) et (BD). De même, la droite (OP) contient le point P2, intersection de (LQ) et (MR).
 Télécharger la figure GéoPlan vecten_3.g2w Télécharger la figure GéoPlan vecten_3.g2w
|
6.d. Extriangles - triangles extérieurs
Pour un triangle ABC quelconque, on trace la figure d'Euclide dite du « moulin à vent », en plaçant à l'extérieur trois carrés construits à partir des trois côtés du triangle.
En joignant les extrémités libres des carrés, on trouve trois nouveaux triangles : les extriangles.
Comparer l'aire de ces triangles à celle du triangle ABC.
Solution
Chacun des trois triangles extérieurs a la même aire que le triangle ABC.
Démonstration par calcul d'aire
Aire(ABC) = 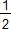 CB × CA sin(BCA) = CB × CA sin(BCA) = 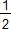 ab sin(BCA) ab sin(BCA)
Par exemple Aire(CNP) = 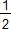 CN × CP sin(NCP) = CN × CP sin(NCP) = 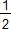 ab sin(NCP). ab sin(NCP).
Ces deux aires sont égales car les angles BCA et NCP sont supplémentaires et ont même sinus.
Autre démonstration par rotation
Pour le montrer par exemple pour le triangle CNP, il suffit d'opérer une rotation de 90° du triangle autour de son sommet C.
Le point N a pour image K, la base CK vient dans le prolongement de BC, avec la même longueur.
Le point P a pour image A, ce qui entraîne que la hauteur, issue de A du triangle ACK, est la même que celle issue de A du triangle ABC.
Les triangles ABC et ACK ayant même longueur de la base et même hauteur, ont même aire.
Le triangle CNP et son image ACK par la rotation ont même aire.
Le triangle CNP a même aire que le triangle de référence.
 Figure interactive dans GeoGebraTube : triangles extérieurs - extriangles Figure interactive dans GeoGebraTube : triangles extérieurs - extriangles
|
Médiatrices
Les médiatrices des côtés des triangles extérieurs ARS, BSM, BFL, côtés non adjacents aux carrés, sont concourantes.
|
|
Définition
La symédiane en O du triangle BOA est la droite (d) telle que cette droite (d) et la médiane issue de O ont pour bissectrice la bissectrice de BÔA.
Les trois symédianes d'un triangle sont concourantes. Leur point de concours L est le point de Lemoine ou point symédian du triangle.
Construction des symédianes avec trois carrés
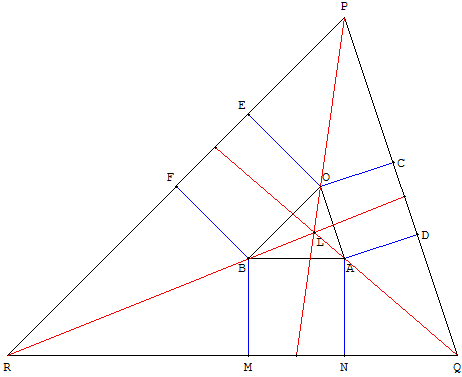
Trois carrés OADC, OEFB et ABMN à l'extérieur du triangle BOA.
Les prolongements des quatrièmes côtés de ces carrés définissent un triangle TUV :
les droites (CD) et (EF) se coupent en P,
les droites (CD) et (MN) se coupent en Q,
les droites (EF) et (MN) se coupent en R.
Le triangle RPQ est le triangle de Grèbe du triangle BOA.
Les droites (OP), (AQ) et (BR) sont les symédianes des triangles BOA et RPQ.
Le point de Lemoine L, du triangle BOA, est aussi le point de Lemoine du triangle RPQ, et réciproquement.
L'homothétie, de centre L, qui transforme B en R, transforme le triangle BOA en RPQ.
 Télécharger la figure GéoPlan vecten_4.g2w Télécharger la figure GéoPlan vecten_4.g2w
|
Problème de Grèbe
Inscrire trois carrés dans un triangle donné PQR.
Deux des sommets de chacun des carrés servent de liaison entre les trois carrés, qui se touchent ainsi par deux coins.
Chaque carré a ses deux autres sommets sur le même côté du triangle donné.
Construction théorique
Tracer le point de Lemoine L, du triangle PQR.
Les carrés cherchés sont alors inscrits chacun séparément dans les triangles LRP, LPQ et LQR, d'où la construction avec des grands carrés le long des côtés de PQR.
Construction pratique
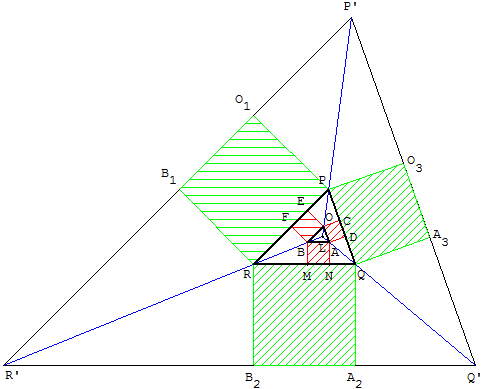
La construction consiste à tracer trois grands carrés à l'extérieur du triangle donné, permettant de trouver le triangle de Grèbe de PQR, puis d'en déduire le triangle OBA qui a PQR comme triangle de Grèbe.
Les côtés des carrés extérieurs au triangle PQR déterminent le triangle de Grèbe P’Q’R’.
Les triangles P’Q’R’ et PQR ont leurs côtés deux à deux parallèles.
Une homothétie de centre L, le point d'intersection des droites (P’P) et (Q’Q), transforme le triangle P’Q’R’ en PQR.
Le point L est le point de Lemoine du triangle PQR.
Cette homothétie transforme le triangle PQR en un triangle OBA.
O3 et A3 sont transformés en C et D ; le carré PQA3O3 est transformé en OADC.
On obtient de même les carrés OEFB et ABMN.
Les trois carrés OADC, OEFB et ABMN, inscrit à l'intérieur du triangle PQR, sont donc la solution du problème de Grèbe.
 Télécharger la figure GéoPlan carres_ds_triangle.g2w Télécharger la figure GéoPlan carres_ds_triangle.g2w
|
|
Sangaku : inscrire trois carrés dans un triangle donné
Deux des sommets de chacun des carrés servent de liaison entre les trois carrés, qui se touchent ainsi par deux coins. Chaque carré a ses deux autres sommets sur deux côtés différents du triangle donné.
Philippe Chevanne (le théorème de Grèbe) fait remarquer que les médianes du triangle intérieur ABC sont perpendiculaires aux côtés du triangle donné PQR.
Faire la construction d'une figure semblable en procédant à l'envers : pour construire les carrés à l'intérieur de PQR, tracer trois carrés à l'extérieur d'un triangle A’B’C’, aux côtés perpendiculaires aux côtés du triangle donné, semblable à ABC.
 Figure interactive dans GeoGebraTube : carrés de Malfatti Figure interactive dans GeoGebraTube : carrés de Malfatti
Construction
À partir d'un point G’ convenablement choisi, tracer trois droites perpendiculaires aux côtés de PQR.
Construire un triangle A’B’C’ tel que ces trois perpendiculaires soient les médianes du triangle A’B’C’, pour cela :
– placer un point A’, distinct de G’, sur la perpendiculaire à (QR),
– tracer le point K, symétrique de A’ par rapport à G’,
– sur les deux autres perpendiculaires, tracer le parallélogramme G’B’KC’ de diagonale [G’K].
À l'extérieur du triangle A’B’C’, construire trois carrés, puis le triangle P’Q’R’ dont les côtés contiennent les sommets externes de ces carrés.
Les droites (PP’) et (QQ’) sont concourantes en S, centre de l'homothétie qui transforme le triangle P’Q’R’ en PQR.
En déduire ABC comme image de A’B’C’ par cette homothétie et tracer les trois carrés inscrits dans PQR.
Voir, cercles de Malfatti : trois cercles tangents, inscrits dans un triangle
Remplir un cercle avec des carrés
|
6.g. Triangle tangentiel
BOA est un triangle donné, RPQ son triangle de Grèbe et L le point de Lemoine
Les tangentes au cercle circonscrit, menées à partir des sommets d'un triangle, se coupent sur les symédianes de ce triangle.
Ces tangentes forment le triangle tangentiel P2Q2R2.
Les sommets du triangle tangentiel sont donc situés sur les symédianes.
Le point de Lemoine L est le point de Gergonne du triangle tangentiel.
 Télécharger la figure GéoPlan vecten_5.g2w Télécharger la figure GéoPlan vecten_5.g2w
|
|
Lemoine Émile, mathématicien français
spécialiste de la géométrie du triangle, 1840- 1912
Les distances du point de Lemoine aux trois côtés du triangle sont proportionnelles à ses côtés.
Le point de Lemoine du triangle BOA, de côtés a = OA, b = OB
et c = AB est le barycentre du système pondéré (A, b2) ; (B, a2) ; (O, c2).
C'est le point dont la somme des carrés des distances aux côtés du triangle est minimale.
La droite passant par le point de Lemoine et le centre du cercle circonscrit s'appelle l'axe de Brocard du triangle
Le cercle ayant pour diamètre [LO] (L point de Lemoine et O centre du cercle circonscrit) s'appelle le cercle de Brocard et contient les points de Brocard du triangle.
Voir : cercles de Tücker
Bibliographie : la figure de Vecten - Jean-Louis Ayme
|
|
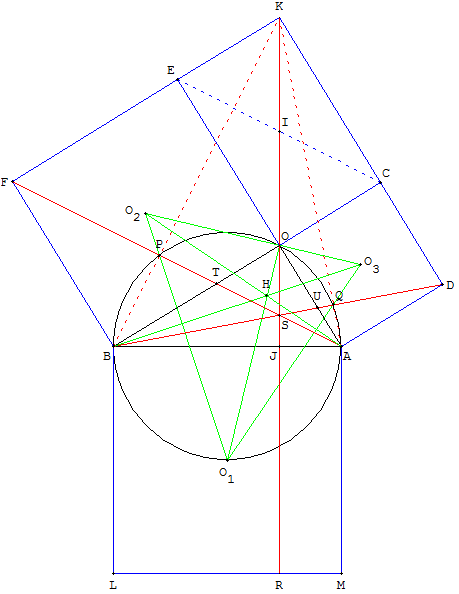
La figure utilisée par Euclide, pour la démonstration du théorème de Pythagore, suggère des résultats inattendus.
Le point O est sur la droite (O2O3) et [OO1] est la hauteur du triangle O1O2O3, issue de O1.
[O2A] et [O3B] sont les deux autres hauteurs.
AF et BK sont égaux et orthogonaux. Les droites (AF), (BK) et (O1O2) sont concourantes en un point P situé sur le cercle circonscrit.
De même (BD), (AK) et (O1O3) sont concourante en Q situé le cercle circonscrit.
Enfin, les triangles rectangles AOT et AEF sont semblables d'où les rapports
OT/EF = AO/ AE donc OT/a = b/(a+b) et OT = ab/(a+b).
Les triangles rectangles BOU et BCD sont semblables d'où les rapports
OU/CD = BO/ BC donc OU/b = a/(a+b) et OU = ab/(a+b).
On a donc OT = OU.
 Télécharger la figure GéoPlan vecten_r.g2w Télécharger la figure GéoPlan vecten_r.g2w
|
|
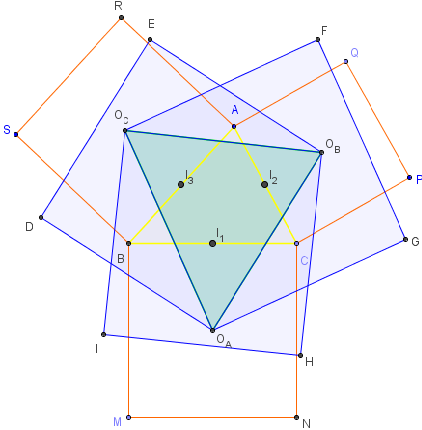
OA, OB, OC sont les centres des trois carrés construits à l'extérieur du triangle ABC.
I1, I2, I3 sont les centres des trois carrés construits intérieurement sur les côtés du triangle de Vecten OAOBOC.
Les points I1, I2 et I3 sont les milieux des côtés du triangle ABC.
 Figure interactive dans GeoGebraTube : théorème de Neuberg Figure interactive dans GeoGebraTube : théorème de Neuberg
Démonstration
Soit C’ le milieu de [AB].
Nous avons démontré ci-dessus que le triangle OAC’OB est rectangle isocèle (la rotation de centre C et d'angle 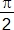 transforme [PB] en [AN] ; transforme [PB] en [AN] ;
leurs moitiés [C’OA] et [C’OB] sont orthogonales et de même longueur).
Les diagonales du carré OAOBED sont perpendiculaires et se coupent en leur milieu I3. Le triangle OAI3OB est rectangle isocèle.
Les deux triangles rectangles isocèles sont identiques.
Le centre I3 est le milieu C’ de [AB].
Et il en est de même des autres centres I1 et I2.
Voir le tracé des points OA, OB, OC avec trois triangles rectangles isocèles autour de ABC.
Figure exportée dans WikiPédia : théorème de Neuberg
|
Quatre carrés autour d'un quadrilatère
Moulin à vent de Van Aubel
De : Aubel tetragon
Construction de quatre carrés à l'extérieur d'un quadrilatère ABCD.
Théorème de Van Aubel
Les segments [PR] et [QS], qui joignent les centres des carrés opposés, sont orthogonaux et de même longueur.
Si le quadrilatère ABCD est convexe, le quadrilatère PQRS est un pseudo-carré.
 Figure interactive dans GeoGebraTube : moulin à vent de Van Aubel Figure interactive dans GeoGebraTube : moulin à vent de Van Aubel
Démonstration du théorème de Van Aubel
Soit I, J, K et L les milieux des côtés de ABCD et  la rotation vectorielle d'angle la rotation vectorielle d'angle 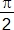 . .
On a : 2 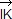 = 2 = 2 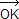 – 2 – 2 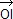 = ( = (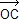 + + 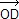 ) – ( ) – (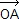 + + 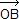 ) = ) = 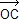 – – 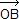 + + 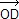 – – 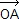 = = 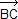 + + 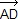 , ,
2 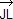 = 2 = 2 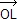 – 2 – 2 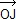 = = 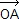 + + 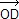 – – 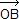 – – 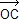 = = 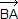 + + 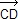 . .
 (2 (2 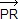 ) = ) =  (2 (2 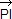 ) + ) +  (2 (2 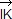 ) + ) +  (2 (2 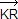 ) )
= 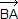 + +  ( (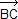 + + 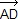 ) + ) + 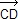
= 2 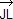 + +  ( (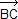 ) + ) +  ( (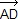 ) )
= 2 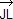 + 2 + 2 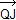 + 2 + 2 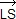
= 2 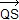 . .
On a donc  ( (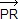 ) = ) = 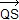 , d'où l'orthogonalité et l'égalité des longueurs de [PR] et [QS]. , d'où l'orthogonalité et l'égalité des longueurs de [PR] et [QS].
Nombres complexes : bac S national 2005
Les centres des carrés permettent de former quatre triangles rectangles isocèles à l'extérieur du quadrilatère.
WikiPédia :
les deux théorèmes de Van Aubel
Voir aussi : droite de Van Aubel dans le triangle
|
8.b. Carré de Thébault
Théorème de Thébault
Construction de quatre carrés à l'extérieur d'un parallélogramme ABCD.
Le quadrilatère PQRS formé par les centres des carrés est un carré.
 Figure interactive dans GeoGebraTube : théorème de Thébault avec 4 carrés Figure interactive dans GeoGebraTube : théorème de Thébault avec 4 carrés
Victor Thébault 1882-1960
Preuve
En effet, la rotation de centre R et d'angle 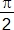 transforme C en D, B en D2, le carré de côté [CB] a pour image le carré de côté [DA]. transforme C en D, B en D2, le carré de côté [CB] a pour image le carré de côté [DA].
Donc, Q a pour image S, soit RQ = RS et l'angle QRS est droit. QRS est un triangle rectangle isocèle en R.
De même, par la rotation de centre P et d'angle 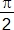 , le carré de côté [DA] a pour image le carré de côté [CB]. , le carré de côté [DA] a pour image le carré de côté [CB].
Donc, S a pour image Q ; PS = PQ et le triangle SPQ est rectangle isocèle en P.
Le quadrilatère PQRS a ses quatre angles droits et des côtés consécutifs égaux : c'est un carré.
Les centres des carrés permettent de construire quatre triangles rectangles isocèles à l'extérieur du parallélogramme ABCD.
|
8.c. Quatre carrés contigus
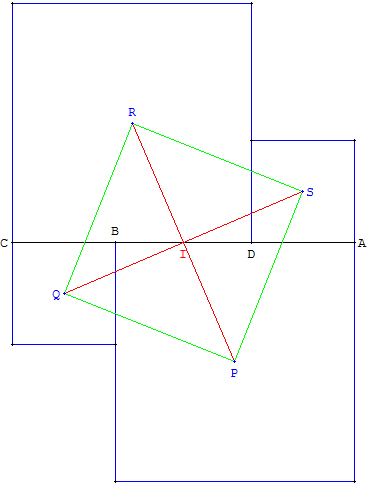
Cas particulier
Soit quatre carrés positionnés le long d'un segment.
Les dimensions des carrés sont les mêmes deux à deux.
Cette figure correspond au cas où le parallélogramme ABCD est aplati :
le point B est un point du segment [AC] de milieu I,
D est alors le symétrique de B par rapport à I.
Le quadrilatère PQRS formé par les centres des carrés est un carré.
 Télécharger la figure GéoPlan pa_aubel.g2w Télécharger la figure GéoPlan pa_aubel.g2w
Autres théorèmes de Thébault :
deux triangles équilatéraux autour d'un carré
le théorème de Thébault − Sawayama
|
 Descartes et les Mathématiques
Descartes et les Mathématiques![]() Sur tablette numérique ou smartphone, bascule automatique vers la version mobile
Sur tablette numérique ou smartphone, bascule automatique vers la version mobile