René Descartes Descartes et les Mathématiques

La géométrie du triangle IV
Lieux géométriques

Lieux des centres : gravité, orthocentre, centre du cercle inscrit ; cercles d'Apollonius.

Sommaire

1. Points remarquables G, H ou I

2. Cercle d'Apollonius

3. Faisceau des cercles d'Apollonius d'un triangle
Le point de Lemoine est sur l'axe radical
4. Lieux et théorèmes de la médiane

Géométrie du triangle

I. Droites remarquables

II. Points caractéristiques

III. Droite et cercle d'Euler

Cercles - Feuerbach

V. Relations métriques

1. Lieux des centres du triangle

geometrie du triangle - lieux des centres

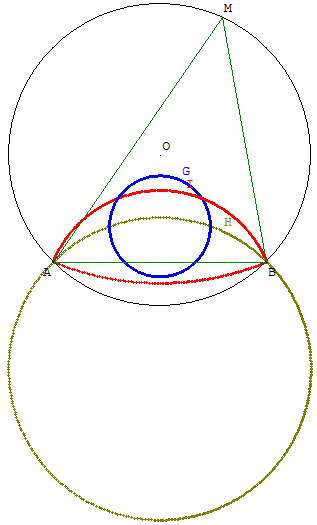
Gravité, orthocentre, centre du cercle inscrit

Étude lorsqu'un des sommets M du triangle ABM parcourt le cercle circonscrit, les deux autres A et B étant fixes.

Le logiciel fait apparaître le lieu de l'orthocentre comme un cercle.
Est-ce une simple apparence ?
Tous les points du cercle sont-ils des points du lieu ?
Comment déterminer le centre et le rayon ?

Document d'accompagnement des programmes de 1^ère S

Sur un cercle c ; A et B sont deux points fixes et M un point variable de c −{A, B}.

Quels sont les lieux géométriques des points remarquables du triangle ABM ?

• En bleu L₁ lieu géométrique de G, centre de gravité,
• En sépia L₂ lieu géométrique de H, orthocentre,
• En rouge L₃ lieu géométrique du centre I du cercle inscrit.

L₂ est le symétrique de c −{A, B} par rapport à (AB).

L₃ se déduit de L₂ par une homothétie de centre O et de rapport .

Lieu de l'orthocentre - cas général : voir parabole

Télécharger la figure GéoPlan lieu_ghi.g2w

2. Cercles d'Apollonius

Apollonius de Perge ou Apollonios de Perga - Astronome et mathématicien grec 262/190 avant J.-C.

Propriétés des bissectrices

Théorème de la bissectrice : tout point de la bissectrice d'un angle est équidistant des côtés de cet angle.

Réciproque du théorème de la bissectrice : la bissectrice d'un angle est l'ensemble des points situés à égale distance des côtés de cet angle

Les bissectrices intérieure et extérieure d'un angle AMB coupent la droite (AB) en I et J.

Définition : Le cercle de diamètre [IJ] est le cercle d'Apollonius associé à l'angle M du triangle AMB.

geometrie du triangle - cercle d'Apollonius - copyright Patrice Debart 2005

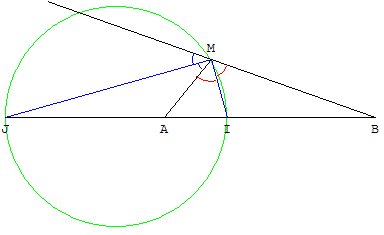
Propriété : Les quatre points (A, B, I, J) forment une division harmonique et

= = .

Théorème — Dans un triangle ABM avec I sur [AB], la droite (MI) est la bissectrice intérieure issue de M si et seulement si = .

Application : lieu des points M tels que = k (k > 0 et k distinct de 1).

Placer les points I et J de (AB) partageant le segment [AB] dans le rapport k.

Le lieu cherché est le cercle d'Apollonius de diamètre [IJ].

Définition : étant donné deux points A et B distincts et un nombre k (k > 0 et k distinct de 1), le cercle d'Apollonius associé à A, B et k est l'ensemble des points M tels que = k.

Démonstration, en 1^ère S, avec les notions de barycentre et de produit scalaire

Élever l'égalité au « carré » MA² = k² MB², transformer les carrés de longueur en produit scalaire ² − k² ² = 0,
factoriser : ( + k ).( − k ) = 0.

Comme k est différent de 1, on trouve deux points : I, barycentre de (A, 1) ; (B, k) et J, barycentre de (A, 1) ; (B, −k).

La formule vectorielle de Leibniz α + β = (α + β) permet d'écrire ( + k ) = (1 + k) et ( − k ) = (1 − k) .

Le produit scalaire nul est donc égal à (1 − k²) . = 0. Les deux vecteurs sont orthogonaux, le point M est sur le cercle de diamètre [IJ].

En posant b = MA et a = MB, alors k = , les droites (MI) et (MJ) sont les bissectrices de l'angle en M du triangle MAB. Le lieu est le cercle d'Apollonius du triangle MAB.

Réciproquement, si M est un point du cercle, le produit scalaire ( + k ).( − k ) est nul, d'où MA² = k² MB².

On a donc = k ; M est un point du lieu.

Télécharger la figure GéoPlan bissect6.g2w

Faisceau harmonique des bissectrices

À ne pas confondre avec le cercle d'Apollonius, tangent aux cercles exinscrits d'un triangle.

Axe radical

Notion disparue de l'enseignement français au lycée

L'axe radical de deux cercles, de centres distincts, est l'ensemble des points qui ont même puissance par rapport à ces deux cercles.
L'axe radical est une droite perpendiculaire à la ligne des centres.
Si les cercles sont sécants, l'axe radical est la droite joignant les points d'intersection.

Voir : géométrie du cercle

Inversions échangeant deux cercles

3. Faisceau des cercles d'Apollonius d'un triangle

geometrie du triangle - faisceau des cercles d'Apollonius - copyright Patrice Debart 2005

ABC est un triangle. Le cercle c₄ de centre O est circonscrit au triangle ABC.

Les bissectrices en A coupent le côté (BC) en I₁ et J₁, le cercle c₁ de centre O₁ a pour diamètre [I₁J₁].
Les bissectrices en B coupent (AC) en I₂ et J₂, le cercle c₂ de centre O₂ a pour diamètre [I₂J₂].
Les bissectrices en C coupent (AB) en I₃ et J₃, le cercle c₃ de centre O₃ a pour diamètre [I₃J₃].

Les trois cercles c₁, c₂ et c₃ d'Apollonius ont deux points communs P et Q, centres isodynamiques du triangle ABC (points X(15) et X(16) dans ETC).
La droite (PQ), axe de Brocard du triangle, est l'axe radical du faisceau de cercles d'Apollonius. Les centres P et Q sont les points de base du faisceau.
Le centre O du cercle circonscrit (c₄) est situé sur l'axe (PQ) ; les points O, L, P, Q forment une division harmonique.

Les centres O₁, O₂ et O₃ sont alignés sur la médiatrice de [PQ], droite de Lemoine du triangle.

Télécharger la figure GéoPlan bissect3.g2w

Article exporté dans WikiPédia : cercles d'Apollonius

Glossaire publimath
À ne pas confondre avec : cercle et point d'Apollonius

Le point de Lemoine est situé sur l'axe radical

geometrie du triangle - point de Lemoine sur l'axe radical - copyright Patrice Debart 2005

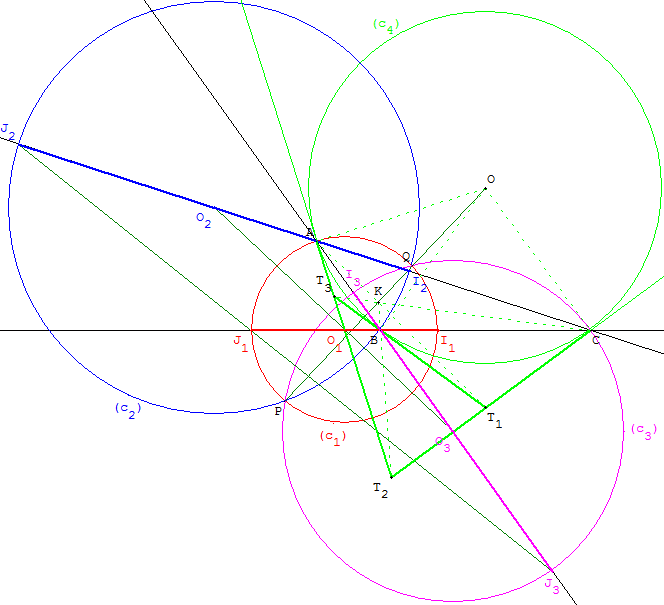
Le rayon (AO de c₄ est perpendiculaire au rayon (AO₁) de c₁. Les cercles c₁ et c₄ sont orthogonaux.
De même, les droites (BO₂) et (CO₃) sont tangentes au cercle circonscrit.

Le cercle circonscrit est orthogonal aux cercles d'Apollonius c₁, c₂ et c₃. Il appartient au faisceau à points limites P et Q, centres isodynamiques du triangle ; P et Q sont les points X(15) et X(16) de ETC.

T₁T₂T₃ est le triangle tangentiel formé par les tangentes au cercle circonscrit. Les droites (AT₁), (BT₂) et (CT₃) sont les symédianes du triangle ABC. Leur point de concours K est le point de Lemoine. Il a même puissance par rapport aux cercles c₁ et c₂.

Les centres isodynamiques, le centre du cercle circonscrit et le point de Lemoine sont alignés sur l'axe radical (PQ) des cercles d'Apollonius c₁, c₂ et c₃.
Cet alignement de points P, Q, O et K est nommé l'axe de Brocard du triangle.

Télécharger la figure GéoPlan apollonius_lemoine.g2w

4. Lieux et théorèmes de la médiane

Soit [AB] un segment de milieu O et longueur a.

Pour un point M du plan, d'après le premier théorème de la médiane, on a MA² + MB² = 2MO² + a²/2.

Pour un réel k tel que k² > a²/2, le lieu des points M tel que MA² + MB² = k² est un cercle dont le centre est le milieu O de [AB].

D'après le troisième théorème de la médiane, on a MA² - MB² = 2., où H est la projection orthogonale de M sur (AB).
Pour que l'on ait MA² - MB² = k, il faut que = k/(2).