Descartes et les Mathématiques
Les quadrilatères au collège en géométrie dynamique
Comment dessiner un quadrilatère ?
Quadrilatère orthodiagonal, cerf-volant, pseudo-carré, quadrilatère inscriptible, antiparallélogramme.
Quadrilatères remarquables
1. Définitions
3. Trapèze
4. Chevron
6. Cerf-volant (géométrie)
7. Pseudo-carré
8.c. Théorème de Ptolémée
8.d. Quadrilatère inscriptible orthodiagonal
Droites remarquables dans un quadrilatère
10. Bissectrices d'un quadrilatère
Sur tablette numérique ou smartphone, bascule automatique vers la version mobile
Quadrilatères remarquables
Quels sont les quadrilatères remarquables ?
1. Définitions
Polygone convexe, concave
en : quadrilateral
de : Viereck
Polygone convexe : polygone plan dont les sommets sont dans un même demi-plan par rapport à n'importe quel côté du polygone.
Polygone concave : polygone qui n'est pas convexe, on dit aussi polygone non convexe.
Quadrilatère convexe, concave, croisé
Un quadrilatère ABCD est un polygone qui a quatre côtés [AB], [BC], [CD] et [DA].
Les quatre points A, B, C, D, situés dans un même plan, tels que trois quelconques d'entre eux ne soient pas alignés, sont les sommets du quadrilatère.
Les points A et C d'une part, B et D d'autre part, sont des sommets opposés.
Les diagonales [AC] et [BD] sont les segments qui joignent deux sommets opposés.
Un quadrilatère découpe le plan en deux zones, une bornée, l'intérieur du quadrilatère (coloriée par GeoGebra) et l'autre est l'extérieur du quadrilatère.
Un quadrilatère est croisé si pour chaque diagonale, les deux autres sommets sont dans un même demi-plan par rapport à cette diagonale ;
les deux diagonales sont à l'extérieur du quadrilatère.
Un quadrilatère croisé est concave (papillon).
Parmi les quadrilatères non croisés, on distingue les quadrilatères convexes et les quadrilatères concaves.
Un quadrilatère est convexe si les deux diagonales sont concourantes ;
pour chaque diagonale, les deux autres sommets sont de part et d'autre de la diagonale ;
les deux diagonales sont à l'intérieur du quadrilatère.
Un quadrilatère est concave si pour au moins diagonale, les deux autres sommets sont dans un même demi-plan par rapport à cette diagonale.;
une diagonale (au moins) est à l'extérieur du quadrilatère.
2. Quadrilatères particuliers
On peut classer les quadrilatères suivant les longueurs des côtés ou des diagonales, le parallélisme des côtés (trapèze, parallélogramme) ou leurs angles, l'orthogonalité des diagonales (cerf-volant),
les éléments de symétrie (antiparallélogramme)
ou l'inscription d'un cercle.
En classe de 5e se fait l'étude du parallélogramme, préparée en 6e par les parallélogrammes particuliers : losange, rectangle ou carré.
Dans cette page, on trouvera l'étude de quadrilatères orthodiagonaux ou inscriptibles.
Quadrilatère quelconque
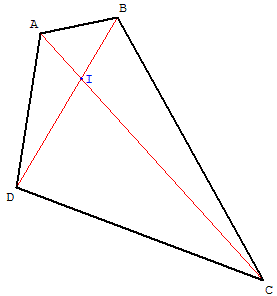
Le quadrilatère ABCD est un polygone convexe qui a :
quatre sommets A, B, C et D ;
quatre côtés [AB], [BC], [CD] et [DA] ;
deux diagonales (AC), (BD) ;
le point d'intersection des diagonales I est le point diagonal.
Télécharger la figure GéoPlan quadrilatere.g2w
Quadrilatère complet
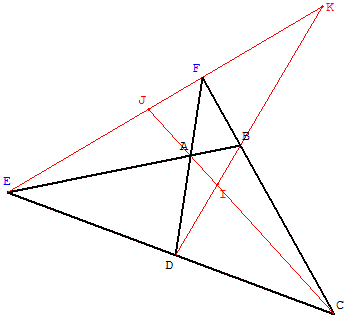
Le quadrilatère complet, formé avec les points A, B, C et D, a :
quatre côtés, situés sur les droites (AB), (CD), (AD) et (BC) ;
six sommets A, B, C, D, E et F ;
trois diagonales (AC), (BD) et (EF) ;
leurs points d'intersection I, J, K sont les trois points diagonaux.
Télécharger les figures GéoPlan quadri_complet.g2w (quadrilatère nu),
quadri_complet_diag.g2w (quadrilatère avec les diagonales)
Retrouver cette figure dans diagonales d'un quadrilatère complet
Quadrangle
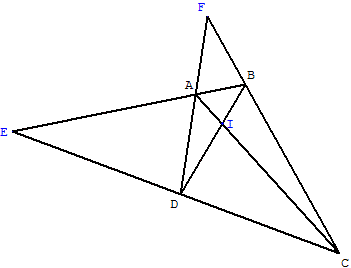
Un quadrangle est la figure formée par quatre points A, B, C, D
tels que trois quelconques d'entre eux ne soient pas alignés :
ce sont les sommets du quadrangle.
Les six droites joignant les points deux à deux sont les côtés du quadrangle.
Si le quadrangle est complet, les trois points diagonaux I, E et F sont les intersections des paires de côtés opposés.
Télécharger la figure GéoPlan quadrangle.g2w
Quadrangle inscriptible, voir : points caractéristiques du triangle
Voir aussi : quadrangle orthocentrique
Définition du quadrilatère complet
Définition : un quadrilatère complet est formé de quatre droites du plan se coupant, deux à deux, en six points.
Remarques (lycée 1ère S - TS) : deux des points peuvent être « à l'infini ». Le quadrilatère est alors un parallélogramme. L'étude de ce cas particulier ne présente pas d'intérêt dans le plan projectif.
Si uniquement un des points est à l'infini, on obtient un trapèze complet.
Ici, nous considérons le quadrilatère complet strict où deux quelconques des quatre droites ne sont pas parallèles, trois quelconques ne sont concourantes :
le quadrilatère complet a quatre côtés, six sommets, trois diagonales et trois points diagonaux.
Lycée 1ère S - TS, voir : plan projectif
Quadrangle quadrilatère complet
Un quadrangle est la figure formée par quatre points A, B, C, D tels que trois quelconques d'entre eux ne soient pas alignés : ce sont les sommets du quadrangle.
Les six droites joignant ces points deux à deux sont les côtés du quadrangle.
Deux côtés qui n'ont pas de sommet en commun sont dits opposés.
Deux côtés opposés (non parallèles) ont un point commun appelé point diagonal du quadrangle.
Un quadrangle complet (dont les côtés ne sont pas parallèles) a quatre sommets, six côtés et trois points diagonaux.
WikiPédia : Quadrilatère
Quadrilatère gauche
C'est un quadrilatère dont les quatre sommets n'appartiennent pas au même plan.
Les côtés et les diagonales forment alors un tétraèdre. L'étude du quadrilatère gauche en lui-même n'a pas de grand intérêt pédagogique.
Nous nous limiterons ici, « avec GéoPlan », aux quadrilatères plans.
Quadrilatères quelconques
Un quadrilatère, autre que les quadrilatères usuels définis dans cette page, est dit quelconque. Un quadrilatère quelconque a ses côtés et ses diagonales de longueurs distinctes, ils ne sont ni parallèles, ni perpendiculaires. Le quadrilatère quelconque n'a pas de symétrie et n'est pas inscrit dans un cercle.
Les quadrilatères quelconques offrent peu d'intérêt, mais permettent de voir ce qui se cache derrière les définitions des quadrilatères usuels.
Technique GéoPlan : calcul de l'aire d'un quadrilatère
Il n'y pas de fonction dans le logiciel pour calculer l'aire d'un quadrilatère. Avec GéoPlan, comme souvent dans la vie courante, on peut le décomposer en deux triangles le long d'une des diagonales. Calculer l'aire de chacun des triangles formés par cette diagonale et deux côtés consécutifs correspondants, puis additionner les deux aires.
s1 aire du triangle ABC (unité de longueur Uoxy)
s2 aire du triangle ADC (unité de longueur Uoxy) s = s1+s2
Il est aussi possible de transformer un quadrilatère convexe en triangle.
3. Trapèze
Définition du trapèze : quadrilatère convexe ayant deux côtés opposés parallèles ;
lorsque le trapèze n'est pas un parallélogramme, les deux côtés parallèles sont les bases : la grande base et la petite base.
Certains imposent comme condition supplémentaire la convexité du quadrilatère, ce qui exclut le « trapèze croisé ».
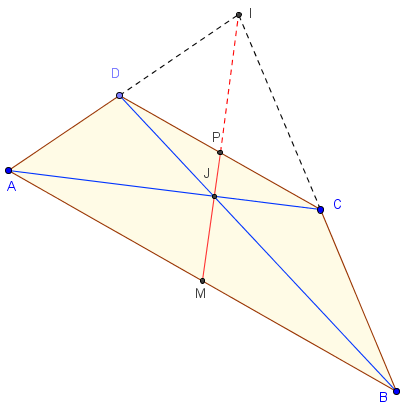
Les côtés non parallèles se coupent en I.
De même, les diagonales sont concourantes en un point J.
Les points I, J et les milieux M et P des côtés parallèles sont alignés (cas particulier du théorème du trapèze complet, classe de 1ère S).
Figure interactive dans GeoGebraTube : Trapèze
Propriétés du trapèze
Un quadrilatère convexe est un trapèze si et seulement s'il possède une paire d'angles consécutifs de somme égale à 180 degrés.
Remarque : Dans un trapèze, la somme de deux angles consécutifs n'est pas toujours égale à 180°. (contre-exemple lorsque le trapèze n'est pas un parallélogramme : les angles adjacents à une même base)
Trapèzes particuliers
Quadrilatère ayant deux angles droits
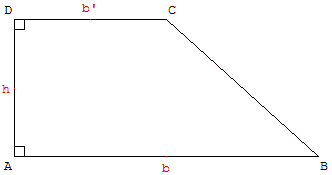
Un trapèze rectangle est un trapèze qui possède un angle droit.
Un trapèze rectangle, qui n'est pas un carré, a exactement deux angles droits.
Télécharger la figure GéoPlan trapeze_rect.g2w
Aire du trapèze rectangle
On applique la formule générale pour l'aire du trapèze :
L'aire d'un trapèze est égale au produit de la moyenne des bases par sa hauteur,
La hauteur est alors égale à la longueur du côté perpendiculaire aux bases, ici égale à AD :
b = AB, b’ = CD, h =AD : Aire(ABCD) = 
× h.
Voir aussi : seconde : partage en deux d'un trapèze rectangle
1S : diagonales orthogonales d'un trapèze rectangle avec le produit scalaire
1L : aire maximum d'un rectangle inscrit dans un trapèze rectangle
Trapèze isocèle
Un quadrilatère est un trapèze isocèle si c'est un trapèze et s'il vérifie l'une des propriétés équivalentes suivantes :
• Les deux côtés opposés, non parallèles, sont de même longueur.
• La médiatrice d'une des bases est axe de symétrie du trapèze. Elle est aussi la médiatrice de l'autre base.
• Deux angles adjacents à une même base sont égaux,
Les angles opposés sont supplémentaires.
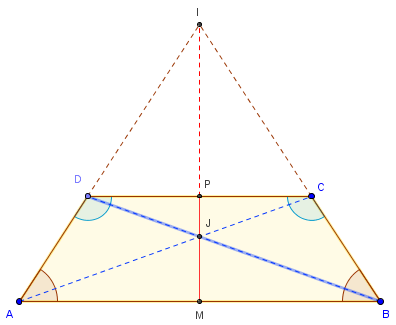
Les côtés non parallèles se coupent en I, point situé sur l'axe de symétrie.
De même, les diagonales sont concourantes en un point J, situé sur l'axe de s target="_blank" rel="nofollow"ymétrie.
Les points I, J et les milieux M et P des côtés parallèles sont alignés sur l'axe de symétrie.
Figure interactive dans GeoGebraTube : Trapèze isocèle
WikiPédia Trapèze
Images trapèze isocèle, fi
Deux droites parallèles coupent un cercle selon un trapèze isocèle ; voir :
• un exemple avec les angles inscrits
• Réciproque : une construction de parallèle
Voir : aire du trapèze
4. Quadrilatère concave : chevron
Quadrilatère non convexe
Quadrilatère concave
Le Chevron ABMC est un exemple de quadrilatère non convexe : la diagonale [BC] est à l'extérieur du quadrilatère.
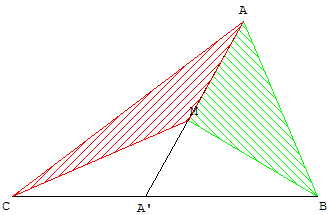
Si M est un point à l'intérieur d'un triangle ABC et A’ le point d'intersection de (AM) et de (BC),
alors le rapport des aires des triangles ABM et ACM est égal au rapport 
.
5. Quadrilatère orthodiagonal
Quadrilatère dont les diagonales sont perpendiculaires.
Quadrilatère orthodiagonal convexe
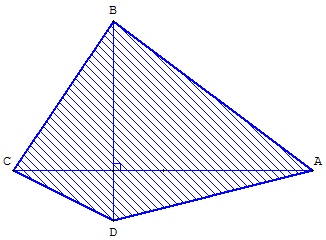
Chevron orthodiagonal non convexe
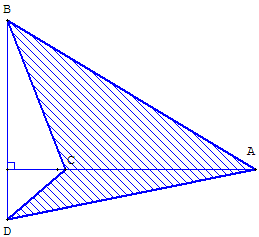
Autre chevron
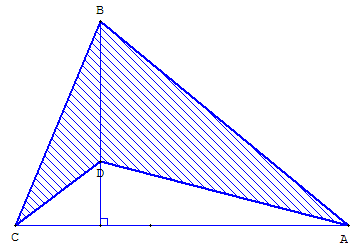
Quadrilatère orthodiagonal inscrit dans un rectangle
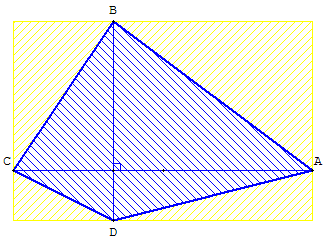
Quadrilatères orthodiagonaux particuliers avec un axe de symétrie: cerf-volant, avec un centre de symétrie : losange
Quadrilatères orthodiagonal particulier inscrit dans un carré : pseudo-carré,
Cas particulier : carré
Chevron inscrit dans un rectangle
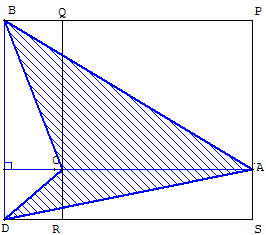
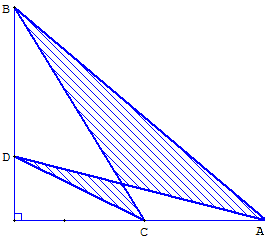
Quadrilatère orthodiagonal croisé.
Télécharger la figure GéoPlan quadri_orthodiagonal.g2w
Calcul de l'aire du quadrilatère orthodiagonal non croisé
Le quadrilatère orthodiagonal convexe ABCD, de la troisième figure ci-dessus, est inscrit dans un rectangle.
L'aire du rectangle est égale au produit des longueurs des diagonales AC × BD.
L'aire du quadrilatère orthodiagonal est alors égale à la moitié : 
AC × BD.
Formule de l'aire d'un quadrilatère orthodiagonal
L'aire d'un quadrilatère orthodiagonal ABCD est égale à la moitié du produit des longueurs des diagonales :
Aire(ABCD) = AC × BD.
(Conforme au cas général étudié au lycée : l'aire d'un quadrilatère convexe est égale au demi-produit des diagonales multiplié par le sinus de l'angle qu'elles forment – Le sinus d'un angle droit vaut 1.)
Ce résultat est encore valable pour les chevrons orthodiagonaux :
par exemple, dans la figure du milieu l'aire du quadrilatère est égale à la somme des aires des triangles ABC et ABD. Leurs aires sont la moitié des aires des rectangles ACQP et ACRS, soit la moitié du rectangle PQRS.
L'aire du quadrilatère orthodiagonal ABCD, non croisé, est encore AC × BD.
Ce calcul ne permet pas de trouver l'aire d'un quadrilatère orthodiagonal croisé – Le décomposer en deux triangles de part et d'autre du point d'intersection des diagonales.
Exemple de calcul d'aire d'un quadrilatère non convexe, non croisé, voir : prenons de la hauteur
6. Cerf-volant isocèle (géométrie)
Classe de sixième
Un quadrilatère convexe, dont une diagonale coupe l’autre en son milieu, est un cerf-volant.
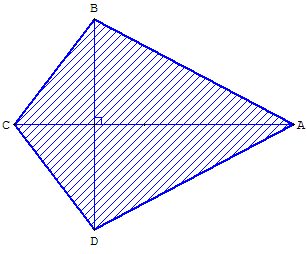
En sixième, on n'étudie pas ce quadrilatère, mais uniquement le cerf-volant isocèle, symétrique par rapport à une diagonale.
En géométrie plane, le cerf-volant isocèle est un quadrilatère orthodiagonal symétrique par rapport à une de ses diagonales.
C'est un quadrilatère isocèle.
On le nomme aussi rhomboïde : quadrilatère en forme de losange.
Dérivé de rhombe, l'ancien nom français du losange, provenant du latin rhombus, mot conservé en anglais pour le losange.
Cerf-volant convexe inscrit dans un rectangle
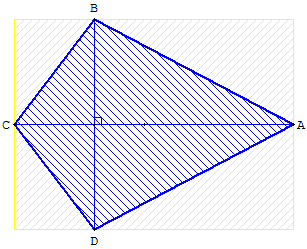
L'aire du cerf-volant ABCD est égale à la moitié de celle du rectangle, de côtés de longueurs AC et BD:
Aire(ABCD) = AC × BD.
Pointe de flèche (ou fer de lance)
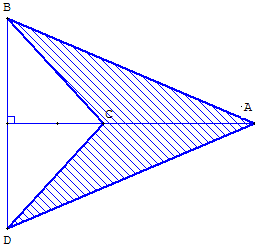
Le cerf-volant isocèle est un quadrilatère tangentiel
Le cerf-volant ABCD étant un quadrilatère orthodiagonal non croisé, son aire est égale à la moitié du produit des longueurs de ses diagonales :
Aire(ABCD) = AC × BD.
La pointe de flèche, cerf-volant concave, ne doit pas être écartée de l'étude des quadrilatères en classe de 6e.
Cerfs-volants particuliers : losange, carré.
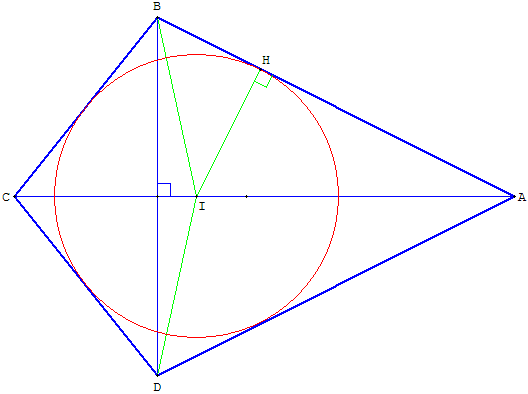
Cercle inscrit dans un cerf-volant
Le cerf-volant est un quadrilatère tangentiel : les quatre côtés sont tangents à un même cercle, inscrit dans le quadrilatère.
Classe de troisième
ABCD est un cerf-volant convexe. Tracer le point I, intersection de la bissectrice de l'angle ABC – angle de côtés de longueurs différentes – avec l'axe de symétrie (AC) du cerf-volant.
I est le centre du cercle inscrit dans le triangle ABC, et en raison de la symétrie, ce cercle est inscrit dans le quadrilatère.
Le cercle inscrit est construit grâce au point H, projection orthogonale de son centre I sur le côté [AB].
Télécharger les figures GéoPlan cerf_volant.g2w,
cerf_volant_cercle_inscrit.g2w
Rétrolien WikiPédia : Cerf-volant
7. Pseudo-carré
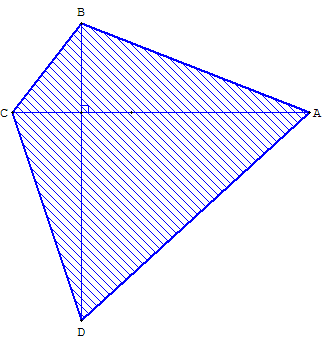
Pseudo-carré : quadrilatère orthodiagonal dont les deux diagonales sont de même longueur.
Télécharger la figure GéoPlan pseudo_carre.g2w
Exemples, voir : Quadrilatères dans la planche à clous
Rétrolien WikiPédia : Pseudo-carré
Voir aussi : droite de Van Aubel dans le triangle
Cas particulier : carré.
Pseudo-carré ; quadrilatère orthodiagonal inscrit dans un carré
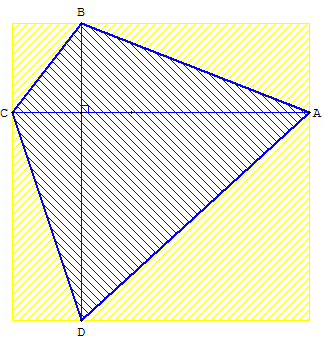
Le pseudo-carré convexe est inscrit dans un carré. L'aire du pseudo-carré ABCD est égale à la moitié de celle du carré, de côté la longueur d'une diagonale :
Aire(ABCD) = AC2.
8. Quadrilatère inscriptible - Points cocycliques
Classe de 3e
Définitions
Des points cocycliques sont situés sur un même cercle.
Un quadrilatère est inscriptible si les quatre sommets sont cocycliques.
Un quadrilatère est inscriptible si (et seulement si) deux angles opposés sont égaux ou supplémentaires.
Exercice
ABCD est un quadrilatère inscrit, dans un cercle de centre O, tel que l'angle ADC = 72°.
– Calculer l'angle ABC.
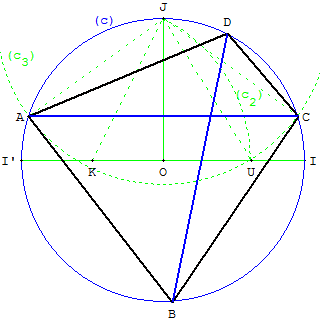
Figure : construire une diagonale [AC] qui sous-tend un angle de 72° avec la construction de Ptolémée
À partir de rayons perpendiculaires d'un cercle (c), tracer le cercle de Ptolémée (c2) de centre K, milieu de [OI’], passant par J. Ce cercle coupe [OI] en U.
Tracer le cercle (c3) de centre J, passant par U. Les points d'intersection des cercles (c) et (c3) déterminent la diagonale [AC].
Placer les deux autres sommets comme points variables sur le cercle (c).
8.a. Quadrilatère convexe
Placer les deux sommets D et B sont de part et d'autre, au-dessus et en dessous, de la diagonale [AC].
Le quadrilatère convexe ABCD est inscriptible : deux angles opposés sont supplémentaires.
ABC + ADC = ABC + 72° = 180°, d'où ABC = 108°.
Télécharger la figure GéoPlanquadri_inscrit_72.g2w
8.b. Quadrilatère croisé (papillon)
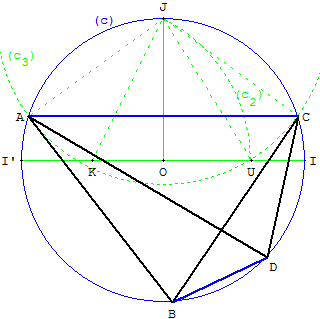
Placer B et D d'un même côté, en dessous de la diagonale [AC].
Le quadrilatère croisé ABCD est inscriptible : deux angles opposés sont de même mesure.
ABC = ADC = 72°.
Pour d'autres figures, voir la page : angles inscrits
8.c. Théorème de Ptolémée
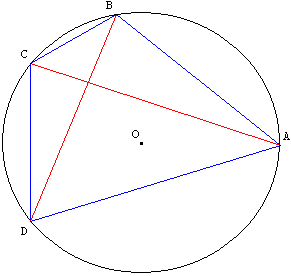
Théorème : un quadrilatère convexe est inscriptible, si et seulement si la somme des produits des côtés opposés est égale au produit des diagonales.
Avec les notations de la figure ci-dessus : AB × CD + BC × DA = AC × BD.
Démonstration, voir : cercle en seconde
Télécharger la figure GéoPlan ptolemee.g2w
8.d. Quadrilatère inscriptible orthodiagonal
Classe de seconde
Théorème de Brahmagupta (mathématicien indien du VIIe siècle) :
si les diagonales d'un quadrilatère inscriptible sont perpendiculaires l'une à l'autre et se coupent en un point O, une droite passant par O et perpendiculaire à l'un quelconque des côtés coupe le côté opposé en son milieu.
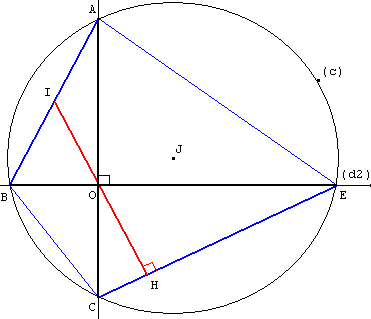
Démonstration, voir : cercle en seconde
Cercle des huit points d'un quadrilatère orthodiagonal, voir en 1ère S : produit scalaire
L'aire du quadrilatère orthodiagonal, AC × BD, est minimale lorsque le centre J du cercle est situé sur une des diagonales,
elle est maximale lorsque J est sur une des bissectrices de l'angle formé par les diagonales.
Télécharger la figure GéoPlan qua_insc.g2w
8.e. Quadrilatère tangentiel (ou circonscriptible)
Cercle inscrit
Pour qu'un quadrilatère convexe possède un cercle inscrit, il faut que ses bissectrices soient concourantes. Leur point d'intersection est alors le centre du cercle.
Un point de ce cercle se trouve en traçant la projection orthogonale du centre, sur l'un des côtés du quadrilatère.
GéoPlan permet de tracer directement ce cercle avec l'instruction : « Créer>Ligne>Cercle>Cercle défini par centre et tangente ».
Quadrilatère tangentiel
Les quatre côtés sont tangents à un même cercle, inscrit dans le quadrilatère.
Théorème de Pitot, démontré en 1725 par l'ingénieur français Henri Pitot : dans un quadrilatère tangentiel, la somme des longueurs de deux côtés opposés est égale à la somme des deux autres.
Pour le démontrer, il suffit de décomposer ces quatre longueurs, selon les points de tangence, en huit longueurs égales deux à deux.
Les cerfs-volants, losanges et carrés sont des quadrilatères tangentiels
Quadrilatère bicentrique : quadrilatère à la fois inscriptible et tangentiel.
9. Antiparallélogramme
Propriétés des quadrilatères croisés
Rappel : les deux diagonales d'un quadrilatère croisé sont à l'extérieur du quadrilatère.
C'est un quadrilatère concave dit papillon.
Pour calculer l'aire, décomposer le papillon en deux triangles de part et d'autre du point d'intersection des côtés.
Papillons particuliers :
• orthodiagonal,
• Inscriptible,
• antiparallélogramme :
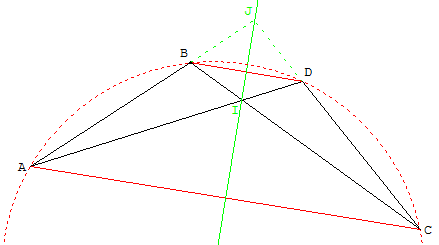
Un antiparallélogramme ABCD est un quadrilatère croisé dont les côtés opposés sont de même longueur, deux à deux :
AB = CD et AD = CB.
Dans un antiparallélogramme les angles opposés ont la même mesure.
Les diagonales (AC) et (BD) sont parallèles.
Télécharger la figure GéoPlan antiparallelogramme.g2w
L'antiparallélogramme admet un axe de symétrie qui est la médiatrice des diagonales.
Deux côtés opposés ont leur point d'intersection situé sur cette médiatrice.
Le quadrilatère convexe ABDC formé par les deux côtés non croisés et les diagonales est un trapèze isocèle.
Un antiparallélogramme est un quadrilatère inscriptible (les quatre sommets sont cocycliques, car les angles ABC et ADC sont égaux).
Un antiparallélogramme, n'étant pas convexe, n'est pas un parallélogramme.
Figure articulée
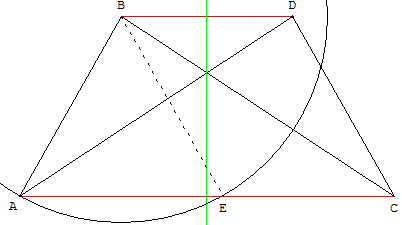
AD = BC = a ; AB = CD = b ; a > b.
Si les sommets A, B, C et D sont articulés, la figure varie,
mais le produit p = DB × CA reste constant.
Cette constante p est égale à a² − b².
Démonstration : elle se fait, après le bac, en considérant la puissance du point C par rapport au cercle de centre B passant par A :
p = CE × CA = DB × CA ; les côtés [CE] et [DB] sont égaux, car CEBD est un parallélogramme.
Télécharger la figure GéoPlan antiparallelogramme_puissance.g2w
Droites remarquables des quadrilatères (au lycée)
10. Bissectrices d'un quadrilatère
Les intersections des bissectrices intérieures d'un quadrilatère forment un quadrilatère inscriptible.
Démonstration
Calcul d'angles en radians au lycée
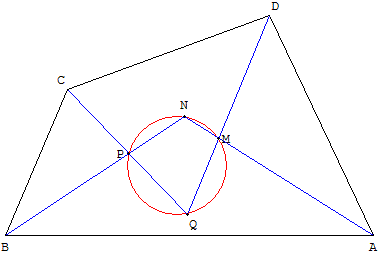
Montrer que s = (
, 
) + (
, 
) = π (modulo 2π).
Par angles égaux (éventuellement opposés par le sommet) on a :
s = (, ) + (, ) = (
, 
) + (
, 
).
La somme des angles d'un triangle étant égale à π, dans les triangles MAD et PCB on a :
s = π − (
, 
) − (
, 
) + π − (
, 
) − (
, 
),
s = (, ) + (, ) + (, ) + (, ) (2π).
Les bissectrices partagent en deux les angles du quadrilatère :
s = [(
, ) + (, 
) + (, 
) + (
, )].
La somme des angles du quadrilatère est 2π :
d'où s = [2π] = π.
Les angles opposés (, ) et (, ) sont supplémentaires. Le quadrilatère MNPQ est inscriptible.
Télécharger la figure GéoPlan bissectrice_quadrilatere.g2w
Retrouver cette figure : turbicône
Cas particulier : bissectrices d'un parallélogramme
11. Médianes d'un quadrilatère
ABCD est un quadrilatère quelconque et I, J, K, L les milieux de ses côtés.
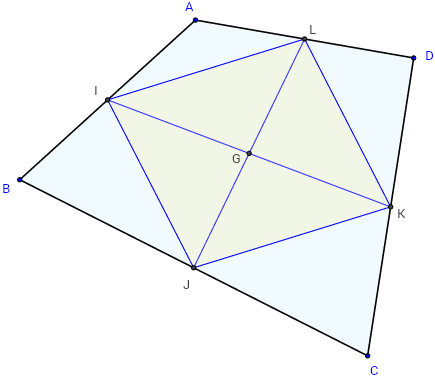
Définition : les médianes d'un quadrilatère (bimédianes) sont les segments reliant les milieux de deux côtés opposés d'un quadrilatère.
Propriété : les deux médianes sont concourants au point G, centre de gravité du quadrilatère. situé au milieu de chaque médiane, car elles sont les diagonales du parallélogramme IJKL de Varignon.
Par abus de langage, on dit parfois que G est le centre du quadrilatère ;
c'est le centre de symétrie du parallélogramme.
Figure interactive dans GeoGebraTube :
Médianes et centre de gravité d'un quadrilatère
Voir aussi le centre d'Euler du quadrilatère.
Voir : théorème de Varignon
Le centre de gravité comme point de concours de trois droites, voir : barycentre.
12. Médiatrices d'un quadrilatère
Les médiatrices d'un quadrilatère ABCD se coupent en P, Q, R et S.
Que dire de PQRS ?
Déplacer les points A, B, C ou D. Étudier les cas particuliers.
Le point P est confondu avec Q, qu'en est-il de R et S. Montrer que les points A, B, C, D sont alors cocycliques sur un cercle de centre P.
Les angles BAD et SPQ sont supplémentaires…
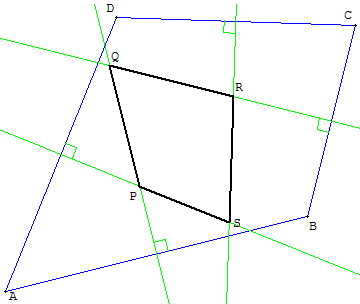
Commande GéoPlan : taper C pour le cercle circonscrit à BCD.
Télécharger la figure GéoPlan quadri_mediatrice.g2w
Médiatrices d'un parallélogramme
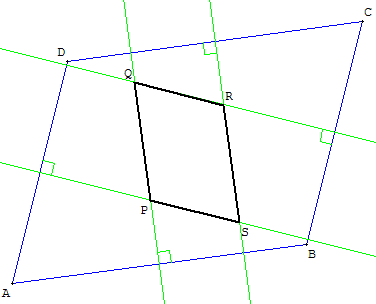
(PQ) et (RS) sont parallèles…
Télécharger la figure GéoPlan para_mediatrice.g2w
Médiatrices d'un cerf-volant(géométrie)
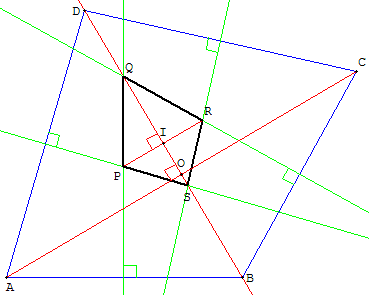
ABCD est un cerf-volant d'axe de symétrie (BD).
Montrer que PQRS est aussi un cerf-volant d'axe de symétrie (BD).
PQRS est aussi un cerf-volant d'axe de symétrie (BD).
Télécharger la figure GéoPlan cerf_volant_mediatrice.g2w
Médiatrices d'un losange
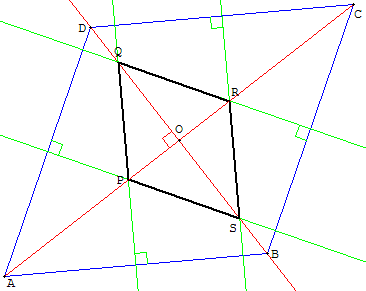
PQRS est aussi un losange ayant les mêmes diagonales que ABCD.
Télécharger la figure GéoPlan losange_mediatrice.g2w
Table des matières
Dans d'autres pages du site
Parallélogramme
Collège : parallélogramme, losange, rectangle
La planche à clous comme géoplan
Observer des quadrilatères particuliers au collège
Téléchargement des anciennes versions de 2008
Télécharger quadrilatere_college.pdf : ce document au format « .pdf »
La première page de ce document n'est pas une image et la copie ne devrait pas être référencée par Google !
Google considère l'URL originale comme une erreur de type "soft 404", mais référence les copies !
Copyright 2007 - © Patrice Debart
Page no 114, réalisée le 28/11/2007
mise à jour le 30/4/2014