Descartes et les Mathématiques
Les mathématiques de la tarte à la crème
Les problèmes de partage en parts égales
Sélection d'articles sur le partage de surfaces.
Partage d'aires en parties égales
1. Diviser le triangle en 2, 3, 4, 6, 7
2. Diviser le carré en 4, 5
3. Diviser le rectangle en 3
4. Diviser le parallélogramme en 2, 5
6. Diviser le cercle en 2, 3, 4, 6…
7. Partage le demi-cercle en 3, 5…
Dans d'autres pages du site
Diviser en trois
Partage d'un segment en trois : constructions élémentaires,
Pliage d'une feuille en trois parties égales : constructions - pliages
Diviser en quatre
Partage de l'angle d'un triangle en quatre : construction de-ci, de-là
Partager les côtés du carré en quatre
Calculs d'aires au collège
Calculs d'aires en cinquième
Calcul d'aires en seconde
Aires du parallélogramme et du trapèze
Démonstrations avec la méthode des aires :
théorème de Thalès
théorème de Pythagore
Aire d'un quadrilatère non convexe : prenons de la hauteur
Calcul de π dans le papyrus de Rhind : fractions égyptiennes
Calcul d'aire minimum : minimum-maximum
Analyse en option 1ère L - TL
Mobile friendly :
sur tablette numérique ou smartphone,
bascule automatique vers la version mobile
Vingt ans après la chute du mur de Berlin et la fin des utopies socialistes, il semble que le partage équitable n'intéresse plus grand monde.
Reste au géomètre le loisir de se poser le problème du partage en parts égales.
Comme chacun sait, le mathématicien est distrait et une bonne dose de crème chantilly masquera les inégalités éventuelles des découpages !
1. Partages du triangle
1.a. Partage du triangle en deux parties égales
Partage d'un triangle à partir d'un sommet
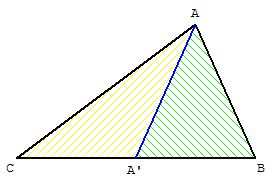
Figure extraite de l'article aire et médiane
Une médiane partage un triangle en deux triangles d'aires égales.
Télécharger la figure GéoPlan prop_medianes.g2w
Partage à partir d'un point M situé sur un des côtés
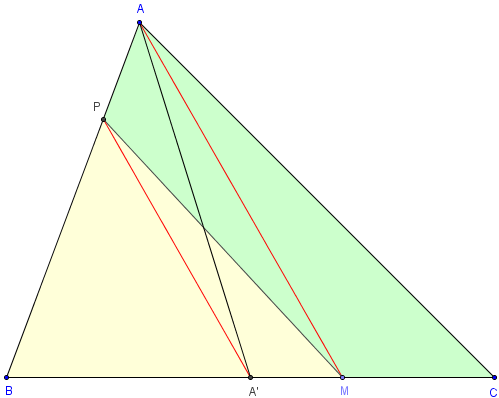
Extrait de l'article olympiades 2004
Deux polygones d'aires égales
Partage d'un triangle ABC par une droite passant par un point M situé sur le côté [BC].
Soit A' le milieu et M un autre point de [BC].
La droite, passant par M, qui divise ABC en deux parties d'aires égales coupe l'un des côtés [AB] ou [AC] en un point P tel que (PA') soit parallèle à (AM).
Figures interactives dans GeoGebra Tube : partage en deux d'un triangle - recherche
1.b. Partage d'un triangle en trois ou en six
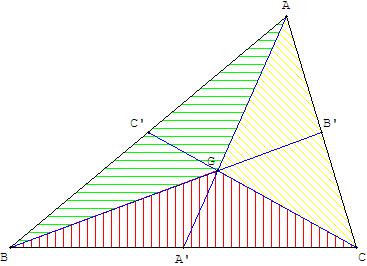
Commet partager un triangle en 3 triangles de même aire
Soit G le centre de gravité d'un triangle ABC, point d'intersection des médianes [AA’], [BB’] et [CC’].
Les trois triangles ABG, BCG et ACG sont d'aires égales.
Corollaire : [GA’] est la médiane de GBC, les triangles GA’B et GA’C ont même aire. On en déduit que G permet le partage du triangle ABC en six triangles d'aires égales.
Extrait de l'article théorème du chevron
Figure interactive dans GeoGebra Tube : médianes d'un triangle
1.c. Partage d'un triangle en quatre
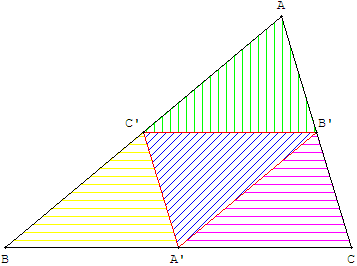
Pour partager un triangle en 4 triangles d'aires égales, tracer le triangle médian.
Les droites des milieux partagent un triangle en quatre triangles homothétiques : dans le rapport 
pour le triangle médian, dans le rapport 
pour les trois autres.
Figure interactive dans GeoGebra Tube : triangle médian
Partage du triangle en huit
Partager chacun des petits triangles ci-dessus en deux avec la médiane (AA’) et les deux parallèles passant par C’ et B’.
Partage du triangle en seize
Le partage en 16 se fait le partage de ces quatre triangles homothétiques, chacun en quatre triangles, seize fois plus petits que ABC.
1.d. Partage d'un triangle en sept triangles de même aire
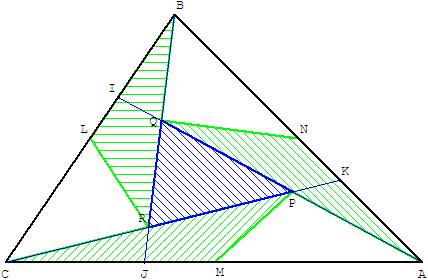
Paragraphe extrait de la page triangles en seconde
Sur les côtés du triangle ABC, placer les points I, J, K tels que :
AK = 
AB,
BI = BC,
CJ = CA.
P, Q et R sont les points d'intersection des droites (AI), (BJ) et (CK).
Le triangle PQR est 7 fois plus petit que le triangle ABC.
Aire(PQR) = Aire(ABC)/7.
Aire(APC) = Aire(AQB) = Aire(BRC) = 2 Aire(ABC)/7.
Avec les milieux M, N et P des côtés du triangle ABC, en traçant les médianes des trois triangles précédents, on obtient six triangles, représentés sur la figure en vert ou en blanc, d'aire égale à celle de PQR.
Télécharger la figure GéoPlan mul_triangle.g2w
2. Partages du carré
Partage d'un carré en quatre
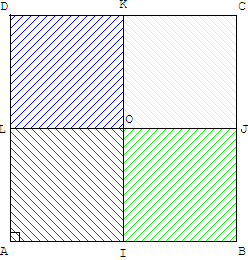
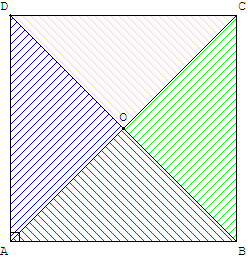
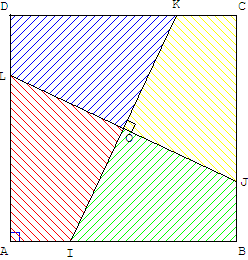
Figure 1: partage par les médiatrices en quatre petits carrés.
Figure 2: partage par les diagonales en quatre triangles rectangles isocèles.
Figure 3: deux droites perpendiculaires, passant par le centre d'un carré, le partagent en quatre quadrilatères égaux.
Voir aussi : puzzle et carrés et puzzle de Périgal
 |
 |
 |
Carré d'aire cinq fois plus petite…
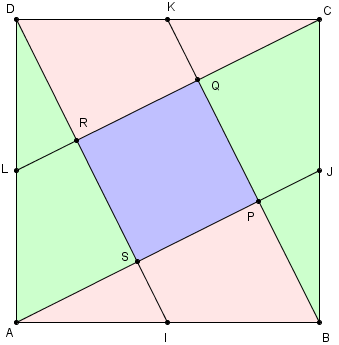
I, J, K et L sont les milieux des côtés d'un carré ABCD (longueur du côté AB = a).
PQRS est un carré, d'aire égale à 
de l'aire de ABCD.
Un découpage de ABCD, en neuf pièces, permet de reconstituer 5 petits carrés en collant aux 4 trapèzes adjacents au carré central PQRS, les 4 triangles rectangles : faire pivoter ces triangles par des rotations de 180° autour des milieux des côtés du grand carré.
Les triangles ABP, BCQ, CDR et DAS ont même aire que PQRS, soit a2.
Figure interactive dans GeoGebra Tube : carré cinq fois plus petit - 5 pièces
Voir aussi : olympiades 2008 - un partage équitable
3. Partages du rectangle en trois
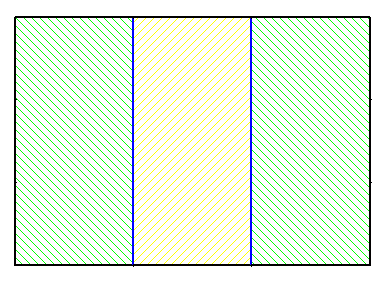
Dans ce découpage classique, la part du milieu a moins de croûte que les deux autres.
Télécharger la figure GéoPlan rectangle_tiers.g2w
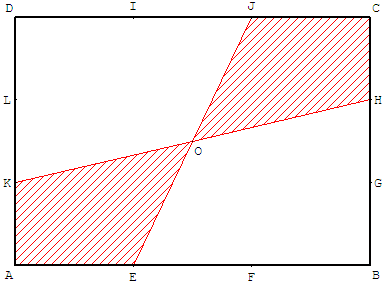
Le géomètre peut proposer cette solution où toutes les parts ont même quantité de croûte.
La troisième part est formée par le polygone croisé hachuré.
Télécharger la figure GéoPlan rectangle_tiers_2.g2w
Partage du rectangle en deux
Le long de la diagonale, partage en deux d'un rectangle avec quatre rectangles : voir construction d'Euclide
4. Partages du parallélogramme
Partage en deux triangles égaux
Une diagonale d'un parallélogramme le partage en deux triangles d'aires égales.
4.a. Partage d'un parallélogramme en deux polygones croisés
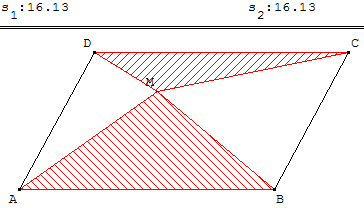
M est un point variable à l'intérieur du parallélogramme ABCD.
La somme des aires des deux triangles hachurés est égale à celle des deux triangles non hachurés.
Paragraphe extrait de la page aire du parallélogramme.
Télécharger la figure GéoPlan para_aire.g2w
4.b. Partage d'un parallélogramme en cinq parties égaules
Paragraphe extrait de la page parallélogramme.
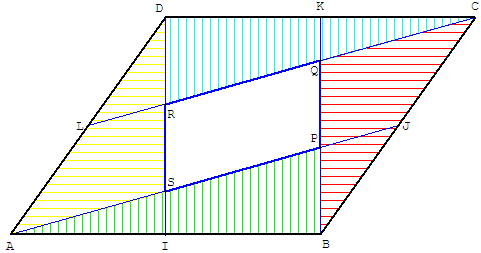
On obtient le petit parallélogramme à partir du grand, en joignant les sommets aux milieux des côtés suivants (dans le sens direct).
Télécharger la figure GéoPlan mul_parall.g2w
5. Partages de quadrilatères
Pour les amateurs de calcul :
Diviser en deux l'aire d'un trapèze
Diviser un trapèze en deux parties d'aires équivalentes par une parallèle aux bases.
Application : Diviser un trapèze en quatre parties égales
Partage en deux d'un trapèze par un sommet
6. Partages du disque
Comment partager un cercle en parts égales.
Tracer un polygone régulier.
6.a. Partage du cercle en 2, 4, 8, 16… parties égales
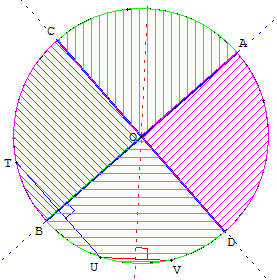
Diviser un cercle en 2 :
Tracez une corde et trouvez-en la médiatrice. C'est un diamètre qui partage le cercle en deux demi-cercles.
Diviser un cercle en 4 parties égales :
Pour un partage en quatre secteurs égaux, sur un diamètre repérer le centre par exemple à l'intersection d'un deuxième diamètre construit comme médiatrice d'une autre corde.
Il suffit enfin de tracer, à partir du centre, la perpendiculaire au premier diamètre.
Télécharger la figure GéoPlan cercle_4parts.g2w
Partage en 8, 16… : il faut ensuite construire successivement la bissectrice de chaque angle créé.
6.b. Partage d'un cercle en trois parties égales
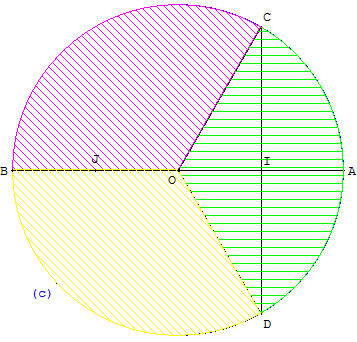
Les partages en 3 et 6 proposés ici et ci-dessous utilisent le fait que :
cos(60°) = .
Diviser un cercle en 3 :
Partager un diamètre en quatre parties égales.
Tracer la perpendiculaire en un des points obtenus, autres que le centre.
Cette perpendiculaire coupe le cercle aux deux points cherchés.
Construction
Sur la figure ci-contre, les points I, O et J partagent le diamètre [AB] en quatre parties égales. La perpendiculaire en I à [AB] coupent le cercle en C et D. Les points B, C et D partagent le cercle en 3.
Télécharger la figure GéoPlan cercle_3parts.g2w
6.c. Partage du cercle en 6
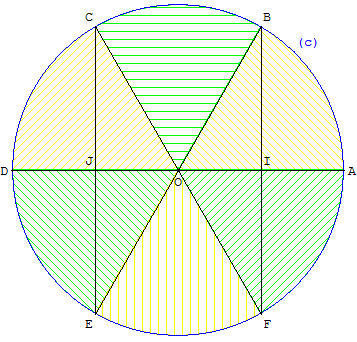
Commet diviser un cercle en six parts égales
Construction d'un hexagone régulier
Pour découper un disque (c) de centre O, en six parties égales, partager en quatre un diamètre [AD] avec les points I milieu de [OA] et J milieu de [OD].
Les perpendiculaires au diamètre, en I et J, rencontrent le cercle (c) aux points cherchés.
Indication
ABCDEF est un hexagone régulier de côtés de même longueur que le rayon du cercle.
OAB est un triangle équilatéral ayant (IB) comme médiatrice.
Télécharger la figure GéoPlan disque_six.g2w
Autres méthodes
6.c.2. Il est aussi possible de prendre la mesure du rayon et de la reporter 5 fois sur le cercle.
6.c.3. À partir du diamètre [AB], construire le cercle de centre A passant par O qui coupe (c) en B et F, puis construire le cercle de centre D passant par O qui coupe (c) en C et E.
Voir : polygones réguliers
Partage en 12, 24… : il faut ensuite construire successivement la bissectrice de chaque angle créé.
Partager un cercle en 9
Tracer un ennéagone régulier, non constructible à la « règle et au compas »,
7. Partages du demi-cercle
7.a. Trisection du demi-cercle par les compagnons
Diviser un demi-cercle en 3 par les compagnons bâtisseurs du Moyen-Âge
Pour couper en trois un demi-cercle de diamètre [BC], les bâtisseurs de cathédrales joignaient le sommet A du triangle équilatéral ABC aux deux points I et J qui divisent en trois le diamètre du demi-cercle.
Les intersections K et L des droites (AI) et (AJ) avec le demi-cercle le divisent en trois.
Télécharger la figure GéoPlan mon_549.g2w
Démonstration : cette solution est exacte
Soit S le symétrique de A par rapport à C et L le milieu de [BS], O le centre du cercle et r le rayon du cercle.
• La médiane [BC] du triangle ABS est égale à la moitié du côté [AS]. On en déduit que le triangle ABS est rectangle en B, il est de plus semi-équilatéral (l'angle en A vaut 60°).
• J est au tiers de la médiane [BC], c'est donc le centre de gravité du triangle ABS et la droite (AJ), médiane issue du sommet A, coupe [BS] en son milieu L.
• Le segment [LC], joignant les milieux des côtés [BS] et [AS], est égal à r moitié de [BA], et est parallèle à (BA), donc perpendiculaire à (BL).
BLC est un triangle rectangle en L. L est donc sur le demi-cercle de diamètre [AB].
• Le triangle OLC est équilatéral de côté r. L'angle CÔL vaut 60° et L divise bien le demi-cercle en trois.
• Par symétrie, il est en est de même pour K.
Télécharger la figure GéoPlan mon_549s.g2w
Indications pour une autre démonstration de cette solution
L'arc BK correspond à une corde [BK] de longueur r égale au rayon du cercle.
En effet, si O est le centre du cercle et P le point d'intersection de (AI) avec la perpendiculaire en B à (BC). Les triangles rectangles IOA et IBP sont semblables avec un rapport de similitude égal à 2 car BI = 2 OI = 
r.
Comme BP = 2OA = 2r
, si Q est le milieu de [BP], [OA] et [QP] sont symétriques par rapport au point K intersection de (AP) et (OQ).
Le triangle rectangle OBQ de côtés BO = r et BQ = r est la moitié d'un triangle équilatéral comme ABC.
L'hypoténuse [OQ] mesure 2r est son milieu K est tel que OK = r, le point K est situé sur le demi-cercle de diamètre [BC].
Par symétrie, il est en est de même pour L, K et L divisent le demi-cercle en trois parties égales.
Télécharger la figure GéoPlan mon_549t.g2w
Voir aussi : trisection de l'angle par les compagnons
Autres méthodes
7.a.2. Comme ci-dessus, partager le diamètre en quatre parties égales. Les perpendiculaires aux deux points autres que le centre coupent le demi-cercle aux deux points cherchés.
7.a.3. Il est aussi possible de prendre la mesure du rayon et de la reporter 2 fois sur le demi-cercle.
7.b. Partage d'un demi-cercle en cinq
Diviser un demi-cercle en 5 parties égales:
Pour partager en cinq un demi-cercle de diamètre [BC], les bâtisseurs de cathédrales du Moyen-Âge joignaient le sommet A du triangle équilatéral ABC aux quatre points qui divisent le diamètre du demi-cercle en cinq parties égales.
La construction n'est pas exacte, mais l'erreur est d'environ 2 %, ce qui rend la méthode acceptable et l'approximation n'est pas perceptible sur un dessin papier.
Il est possible de généraliser cette méthode au partage d'un demi-cercle en n parties égales.
Table des matières
Dans d'autres pages du site
Triangle au collège
Calculs d'aires en 5e
Index Aires
Page no 152, réalisée le 9/10/2009
modifiée le 21/03/2012